• A force is either a push or a pull that one object exerts on another object.

• It can produce, slow down, speed up, stop motion, or change its direction.

0. Previous knowledge

Vectors and scalars

• A vector has magnitude and direction.

• A scalar has just magnitude.

• E.g., speed is a scalar, and velocity is a vector.

Vector diagrams

• In vector diagrams, vector quantities such as forces are represented by an arrow.

• The length of the arrow is proportional to the size of the force.

• The direction of the arrow shows the direction of the force.

• Steps to draw a vector:

  • 1. Choose an appropriate scale

  • 2. Measure the required angle using a protractor from the baseline/second force.

  • 3. Draw an arrow of length proportional to the force using the scale taken.

Adding vectors

Parallel vectors

• If they are in the same direction, they will be added.

• If they are in opposite directions, the resultant will be in the direction of the greater force and its size will be the difference of the two vectors.

• If they are equal and opposite, there will be no resultant.

Non-Parallel vectors

• Tip-to-tail method: redraw one of the vectors, placing the tail of the vector at the tip of the second vector. Join the two corners to get the resultant.

• Parallelogram method: complete the parallelogram, the diagonal of the parallelogram will be the resultant.

1. Movement and position

Speed

• Speed is the distance travelled per unit of time.

• It is a scalar.

  • e.g., 5 m/s.

• It is always positive.

• Speed \: (v) = \frac{distance \: travelled \: (d)}{time \: taken \: (t)}

• Since distance is measured in meters, and time is measured in seconds, speed's unit is metres per second (m/s) or kilometres per hour (km/h).

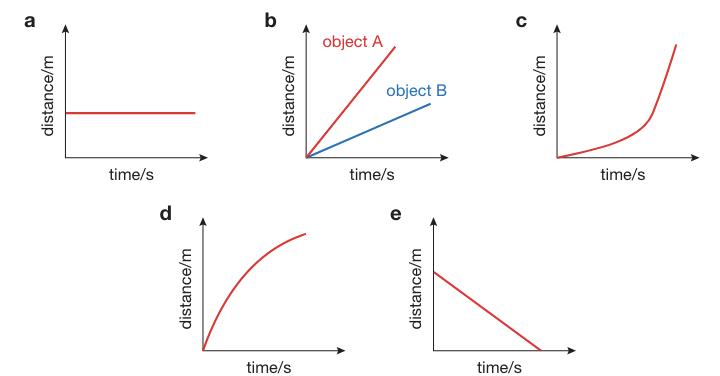
Distance-time graphs

• Distance-time graphs provide a record of how far an object has moved as time has passed.

• Distance travelled is plotted on the vertical axis, and time is plotted on the horizontal axis.

• The line's slope, or gradient, tells us the object's speed.

  • The steeper the line, the greater the speed.

• Acceleration is when an object speeds up, as shown in diagram C.

• Other distance-time graphs are also shown in the picture below:

Velocity

• Unit: m/s (metres per second) or km/h (kilometres per hour).

• Velocity is speed in a given direction, so it is a vector.

  • e.g., 5 m/s east.

  • We not only know how fast something is going but also where it's going.

• It can be negative or positive.

• Velocity \\: (V) = \frac{displacement \\: (d)}{time \\: taken \\: (t)}

• Displacement means distance travelled in a particular direction from a specified point.

Average speed and average velocity

• Speed or velocity refers to a specific time/point of a journey.

• When calculating average speed/velocity, we calculate the speed/velocity of the entire journey.

• This journey may include the resting time in between and any acceleration or deceleration in the journey.

• Average \: speed \: (v) = \frac{distance \: moved \: (d)}{total \: time \: taken \: (t)}

• Average \: velocity \: (v) = \frac{total \: displacement \: (d)}{total \: time \: taken \: (t)}

Acceleration

• Acceleration = (final velocity (v) - initial velocity (u) ) / time taken (t)

• It is a vector.

• Acceleration is the rate of increase in velocity with time.

• It is measured in m/s^2 (meters per second squared).

• Deceleration means slowing down.

  • A negative acceleration simply means deceleration.

• {(Final \: speed \: (vu))}² = {(initial \: speed \ (vi))}² + 2 * acceleration (a) * distance \: moved \: (d)

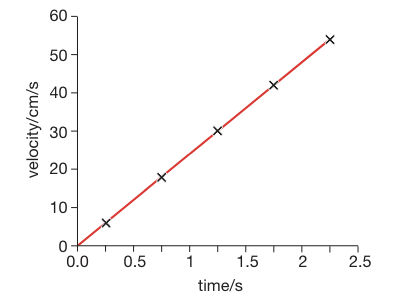
Velocity-time graphs

• The gradient in the picture below is straight, which tells us that the velocity is increasing steadily.

  • This means that the acceleration is uniform.

• Average \: velocity \: (v) = \frac{initial \: velocity \: (vi) + final \: velocity \: (vf)}{2}

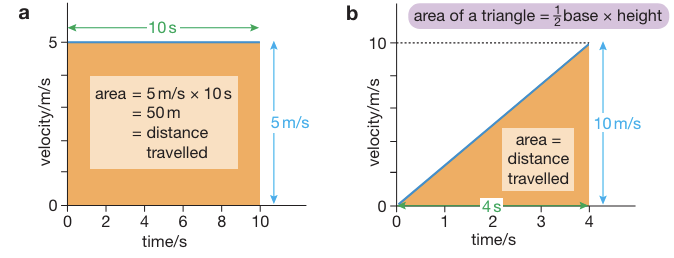
• The area under a velocity-time graph is equal to the distance travelled by the object in a particular time interval.

Circular motion

• When an object is travelling in a circle at constant speed, the velocity is always changing as the direction is constantly changing.

• The resultant force of a circular motion is towards the center of the circle.

2. Forces and Shape

• The unit used to measure force is the Newton (n).

  • A force of one newton will make a mass of one kilogram accelerate at one metre per second squared.

• A force is a vector quantity.

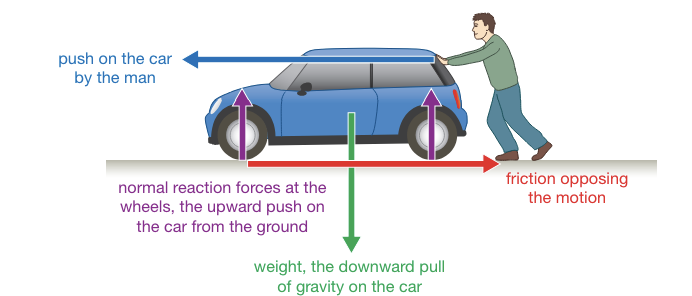
Common forces

• Weight is the pull of the gravitational force on an object.

• The normal force is a reaction force, the upward push on an object from the ground.

• Friction is a force that opposes motion.

Balanced and unbalanced forces

• The resultant force is the sum of all individual forces acting upon an object.

• When the forces acting on something are balanced, the object does not change the way it is moving.

  • Unbalanced forces acting on an object cause it to change the way it is moving.

• Inertial mass is a measure of how difficult it is to change the velocity of an object.

  • Inertial \: mass \: (m) = \frac{force \: (f)}{acceleration \: (a)}

Friction

• Friction is the force that opposes motion between two surfaces in contact.

  • It causes objects moving to slow down and stop.

• The kinetic energy of the moving object is transferred to heat as work is done by the friction force.

• Reducing friction means that machines work more efficiently

  • Increasing friction helps tyres grip the road better.

Changing shapes

• Sometimes, a force can make an object change shape, either permanently or temporarily.

Springs and wires

• Springs are coiled lengths of certain types of metal, which can be stretched or compressed by applying a force to them.

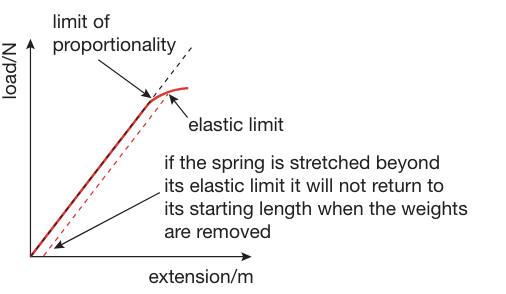
• They obey Hooke’s law, which states that the extension is directly proportional to the force causing it.

  • Hooke’s law only applies until the limit of proportionality, after which the object does not obey the law, and the extension is imbalanced.

  • A straight line on a graph of extension shows the object is obeying Hooke’s law.

• If a spring is stretched beyond its elastic limit, it will not return to its starting length.

• The extension doubles if two springs are connected to each other directly.

• The extension halves a load attached to two springs in parallel as the load is shared.

• Force \: (f) = mass\:(m)*acceleration\:(a)

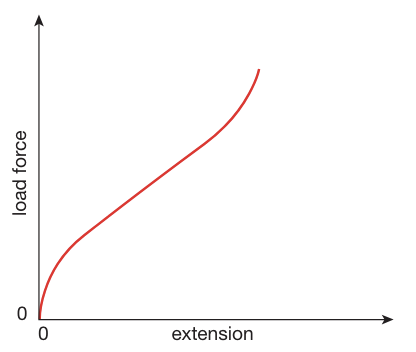
Elastic bands

• Elastic bands are another example of changing objects.

  • They do not follow Hooke’s law.

3. Forces and movement

Force, mass, and acceleration

• The acceleration of an object depends on the size of the unbalanced force and the mass of the object.

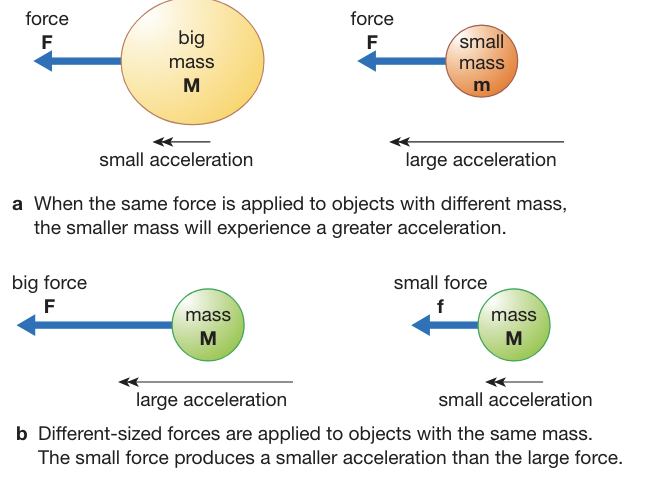
• Acceleration is inversely proportional to mass.

• Force \: (f) = mass\:(m)*acceleration\:(a)

Human Reaction Time

• Human reaction time is the time taken between a stimulus being presented and the initiation of a response by an individual.

• The average human reaction time is 0.25 seconds.

• Factors Affecting Reaction Time:

  • Age and health of the individual.

  • State of alertness and concentration.

  • Influence of drugs or alcohol.

  • Nature of the stimulus (visual, auditory, etc.).

Stopping Distance

• Stopping distance is the total distance covered by a vehicle from the moment the driver perceives a hazard until the vehicle comes to a complete stop.

• Components of stopping distance:

  • Thinking Distance: The distance traveled by the vehicle during the driver's reaction time.​

  • Braking Distance: The distance traveled by the vehicle while the brakes are applied and the vehicle decelerates to a stop.

• Factors affecting stopping distance:

  • Speed of the vehicle.

  • Road surface conditions (dry, wet, icy).

  • Condition of tires and brakes.

  • Reaction time of the driver.

Weight

• The weight of an object is the force that acts on it because of gravity.

• The gravitational field strength is the force that acts on each kilogram of mass.

• Weight \: (w) = mass\:(m)*gravity\:(g)

• Gravity on Earth is approximately 9.81N.

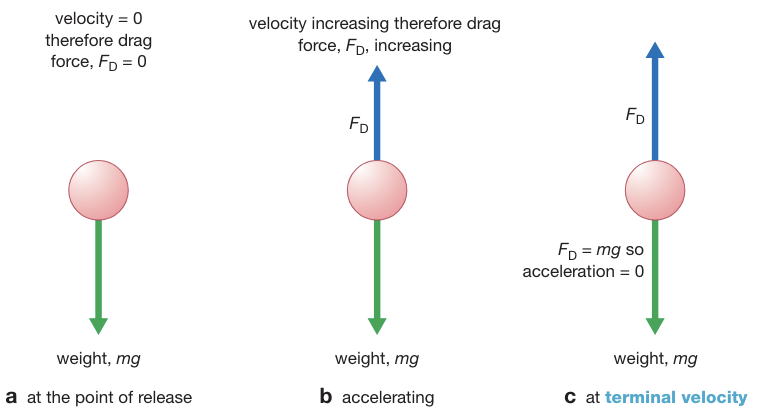
Air resistance and terminal velocity

• Air resistance, or drag, is a frictional force that opposes motion in air. It slows down anything travelling through the air and may also cause the object to heat up.

• The drag coefficient is a measure of how easily an object moves through the air.

• Terminal velocity is when the drag force has increased to the point where it exactly balances the weight force.

• Since there is now no unbalanced force on the object its acceleration is also zero.

Work

• The work done to stop an object is equal to the initial kinetic energy of the object.

• KE=Fd=\frac{1}{2} mu²

4. Momentum

• Momentum is a measure of how difficult it is to stop something that is moving.

• Momentum \: (p) = mass\:(m)*velocity\:(v)

• It is a vector quantity, measured in kilogram metres per second (kg m/s).

Momentum and acceleration

• The rate of change of momentum of an object is proportional to the force applied to the object.

• Force \: (F) = \frac{final \: momentum \: (mf) \: - \: initial \: momentum \: (mi)}{time \: taken \: (t)}

Momentum and collisions

• The total momentum of objects that collide remains the same.

Newton’s Laws of Motion

Newton's first law

• An object at rest remains at rest, and an object in motion remains in motion at constant speed and in a straight line unless acted on by an unbalanced force.

Newton's second law

• When a resultant force acts on an object of a constant mass, the object will accelerate in the direction of the resultant force.

• The product of the mass and acceleration of the object gives the resultant force.

• Force \: (f) = mass\:(m)*acceleration\:(a)

Newton's third law

• Every action has an equal and opposite reaction.

• F₁=F₂

  mass_1 * acceleration_1 = mass_2 * acceleration_2

⠀

5. The turning effect of forces

The moment of a force

• A moment is the turning effect of a force.

• They occur when a force causes an object to rotate about a pivot or hinge.

• The size of the moment is determined by the size of the force and the perpendicular distance from the pivot.

• Moment \: (M) = force \: (f) * perpendicular\:distance\:from\:pivot\:(d)

• The unit of moments is Newton Metres (Nm).

• Opening or closing a door is an example of a moment.

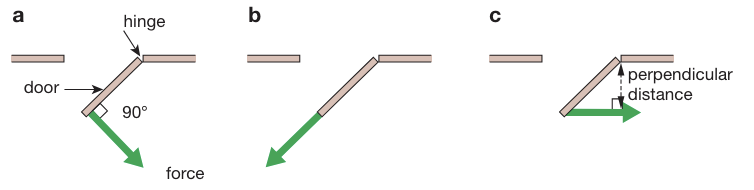
Principle of Moments

• The Principle of Moments states that for an object to be balanced, the clockwise moment must be equal to the anticlockwise moment.

• F_1 * D_1 = F_2 * D_2

Centre of Mass and Stability

• The centre of mass of an object is the point at which the weight of the object acts.

• For symmetrical objects, the centre of mass is at the point of intersection of its symmetries.

• When an object is suspended, its centre of mass will come below it.

• To find the centre of mass of a lamina, it is suspended from a point and a plumb line is hung next to it.

  • A line is drawn using a pencil along the plumb line.

  • This is repeated from multiple points, the point of intersection of the lines is the centre of mass.

• An object is stable when its centre of mass is above its base.

• If the centre of mass is not directly above its base, the object will topple over.

• The lower the centre of mass of an object, the greater the stability.

  • The greater the base area of an object, the greater the stability.