Geometry regents

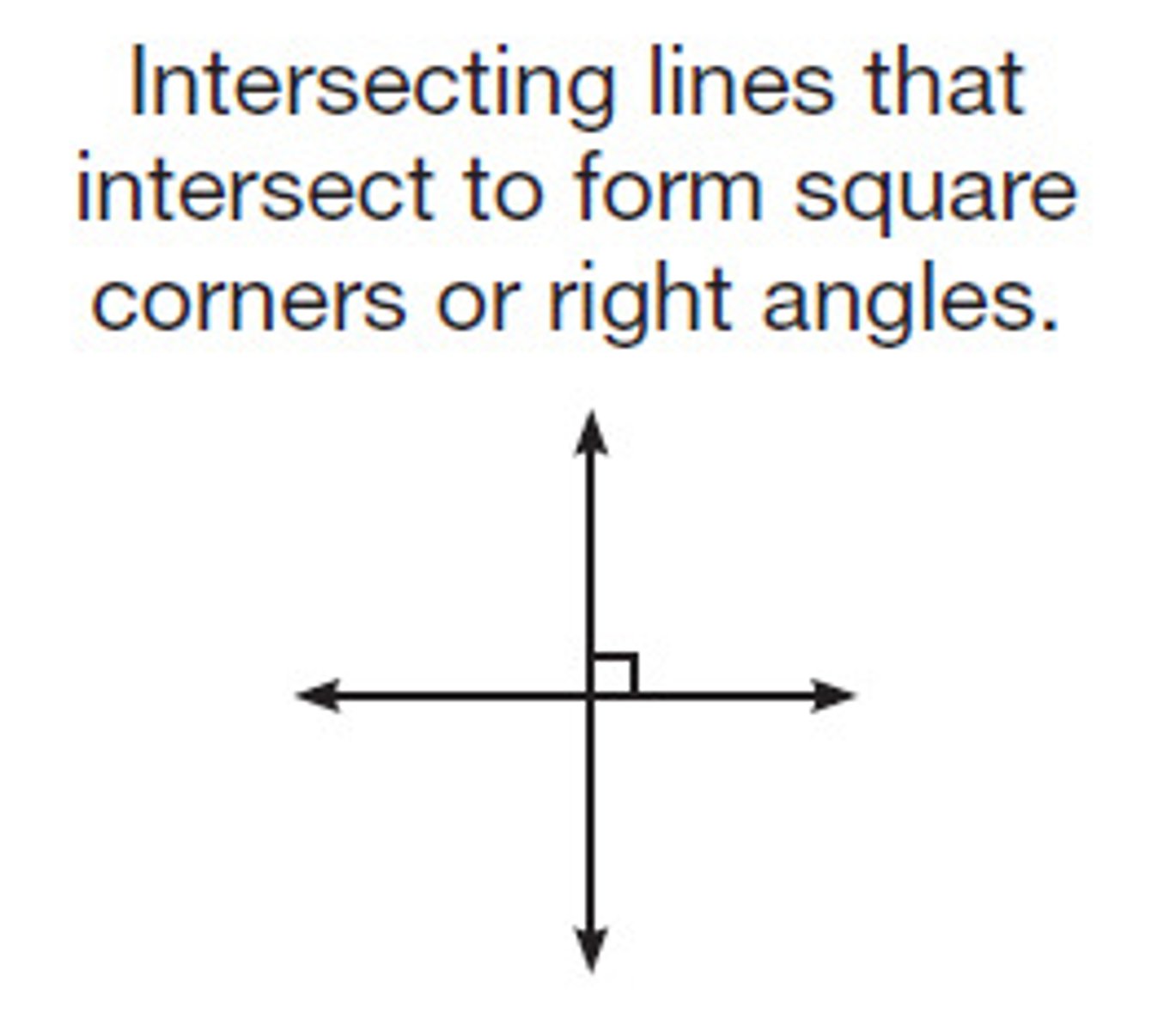
perpendicular lines

form right angles

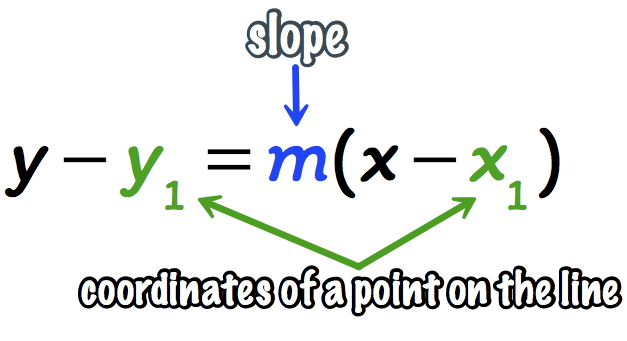
Point slope formula

y - y₁ = m(x - x₁)

If you are given endpoints, find the midpoint of the endpoints first before using this formula.

1. x = 5

2. y = 2

3. y = x

4. x+y = 4

x=5

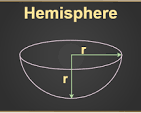
How do you find the height of a hemisphere?

The height is the same as the radius.

How do you find the height of a sphere?

The height is the same as the diameter.

Coordinate geometry: prove ABC is an isosceles right triangle. A(-2,2) B(1,4), C(7,1)

1. Graph figure

2. Complete formulas

   1. AB: d=√(1-(-2))² + (4-(-2))² = √45

   2. BC: d=√(7-1)² + (1-4)² = √45

   3. m of AB = 4-(-2)/1+2 = 2

   4. m of BC = 4-1/1-7 = ½

3. Concluding sentences

   1. Since AB ≅ BC, triangle ABC is isosceles

   2. Since BC ⊥ AB, ABC is a right triangle

Dilation of a line: write the equation of image y=3/2 x-4 after dilation of ¾ centered at the origin.

1. Check if the center of dilation is on the line by plugging it into the original equation.

   1. y=3/2x-4

   2. 0=3/2(0)-4

   3. 0≠-4

2. If the point is on the line, the answer is the same equation as the original line.

   1. Since 0≠-4, the point is not on the line.

3. If not, your answer is a || line with the same slope and a y intercept formed by multiplying the old y intercept by the scale factor.

   1. y intercept: -4×3/4 = -3

   2. slope: since m=3/2, m of || line=3/2

4. Write the equation of the line.

   1. y=3/2x-3

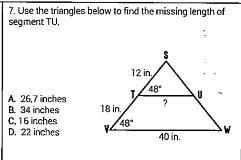
16 in

36

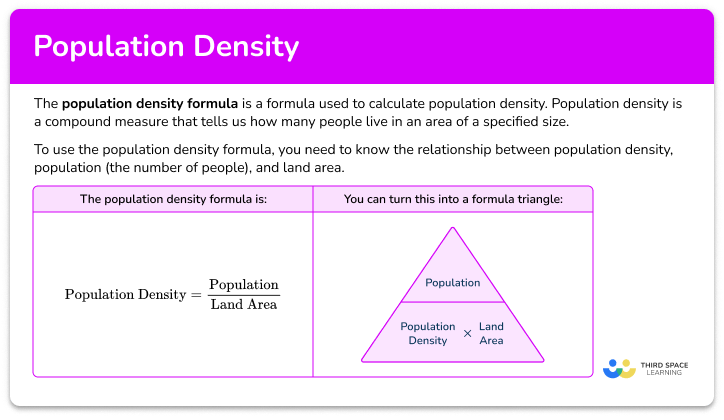
Formula for population density

population density = population/area

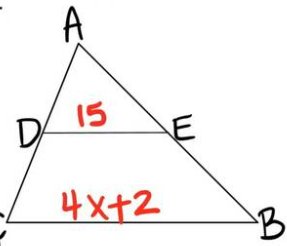
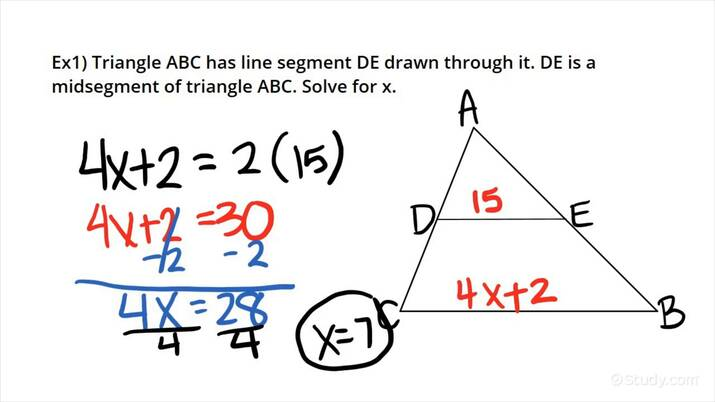
DE is a midsegment of triangle ABC. Find x

Surface area of a square pyramid

a² + 2al

a: side length

l: length

Area of the base of a square pyramid

B = a²

a: side length

Area of triangle (two sides and an angle)

½ absinc

How many sides are in a quadrilateral?

4

How many sides are in a pentagon?

5

How many sides are in a hexagon?

6

How many sides are in a heptagon?

7

How many sides are in a octagon?

8

How many sides are in a nonagon?

9

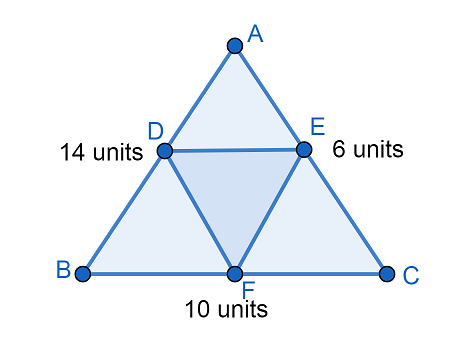
Find the perimeter of the triangle DEF.

15 units

How many sides are in a decagon?

10

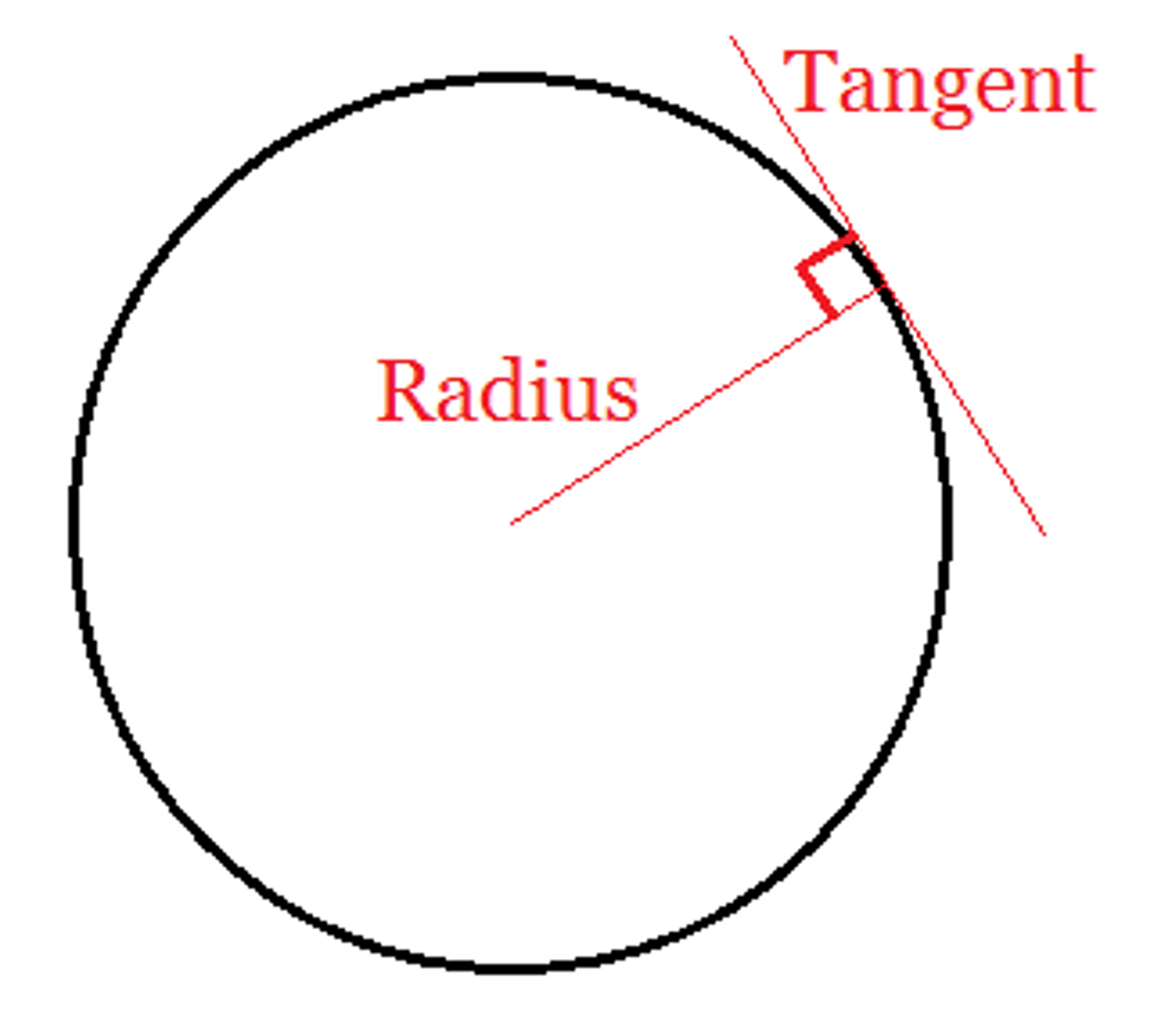
diameters/radii and tangents

form right angles

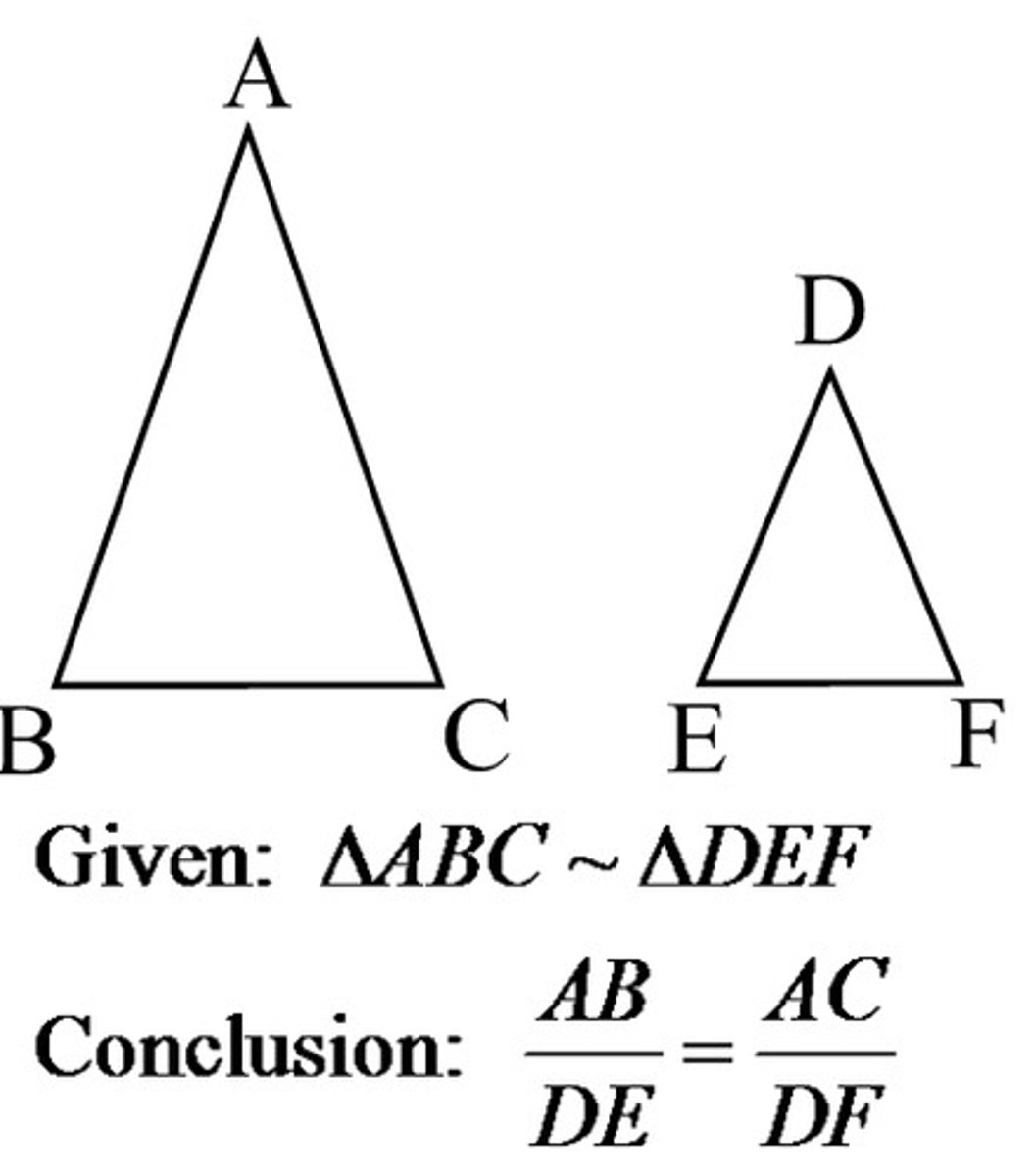
corresponding sides of similar triangles are

in proportion

legs in an isosceles shape are

equal

if 2 parallel lines are cut by a transversal the alternate angles are

congruent

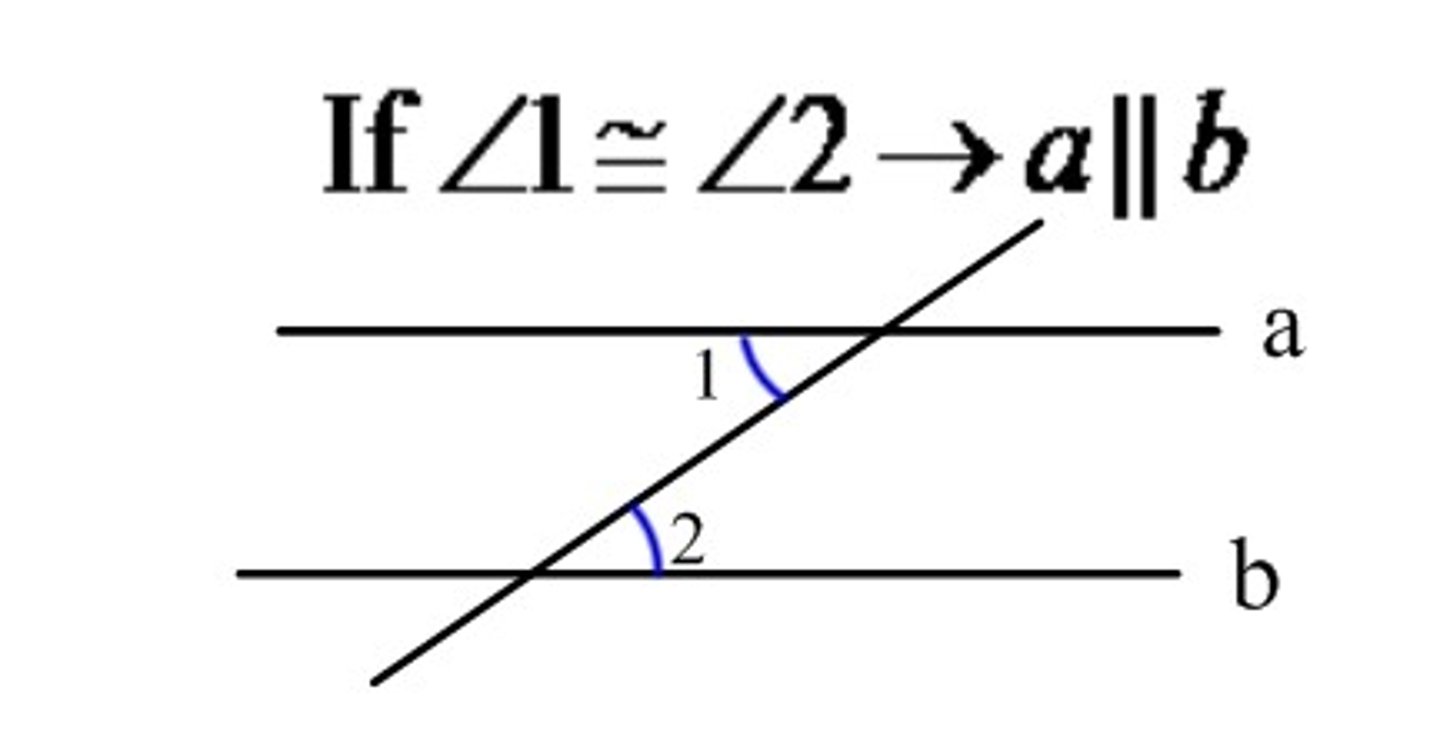
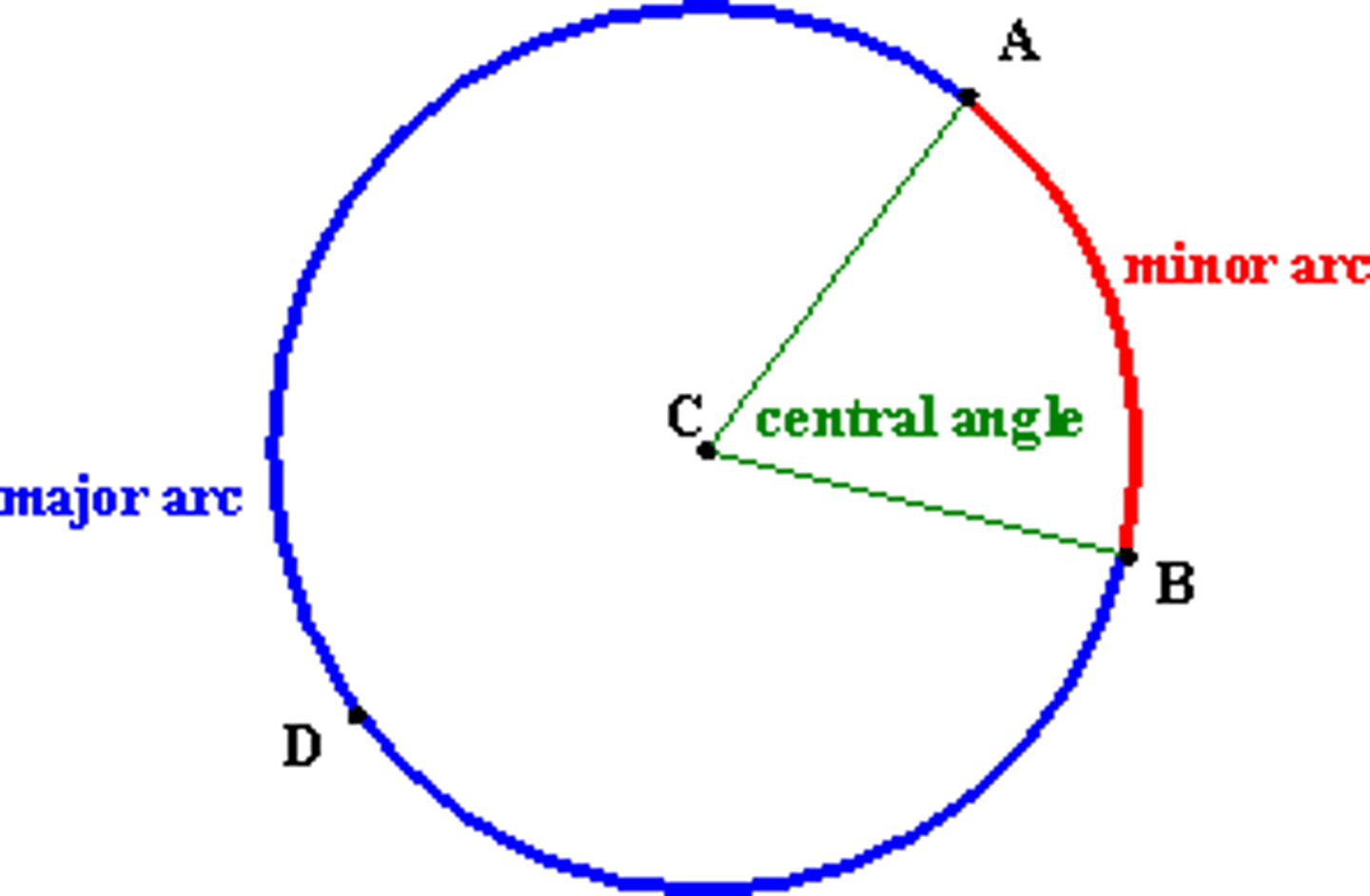
ø is

the measure of the central angle

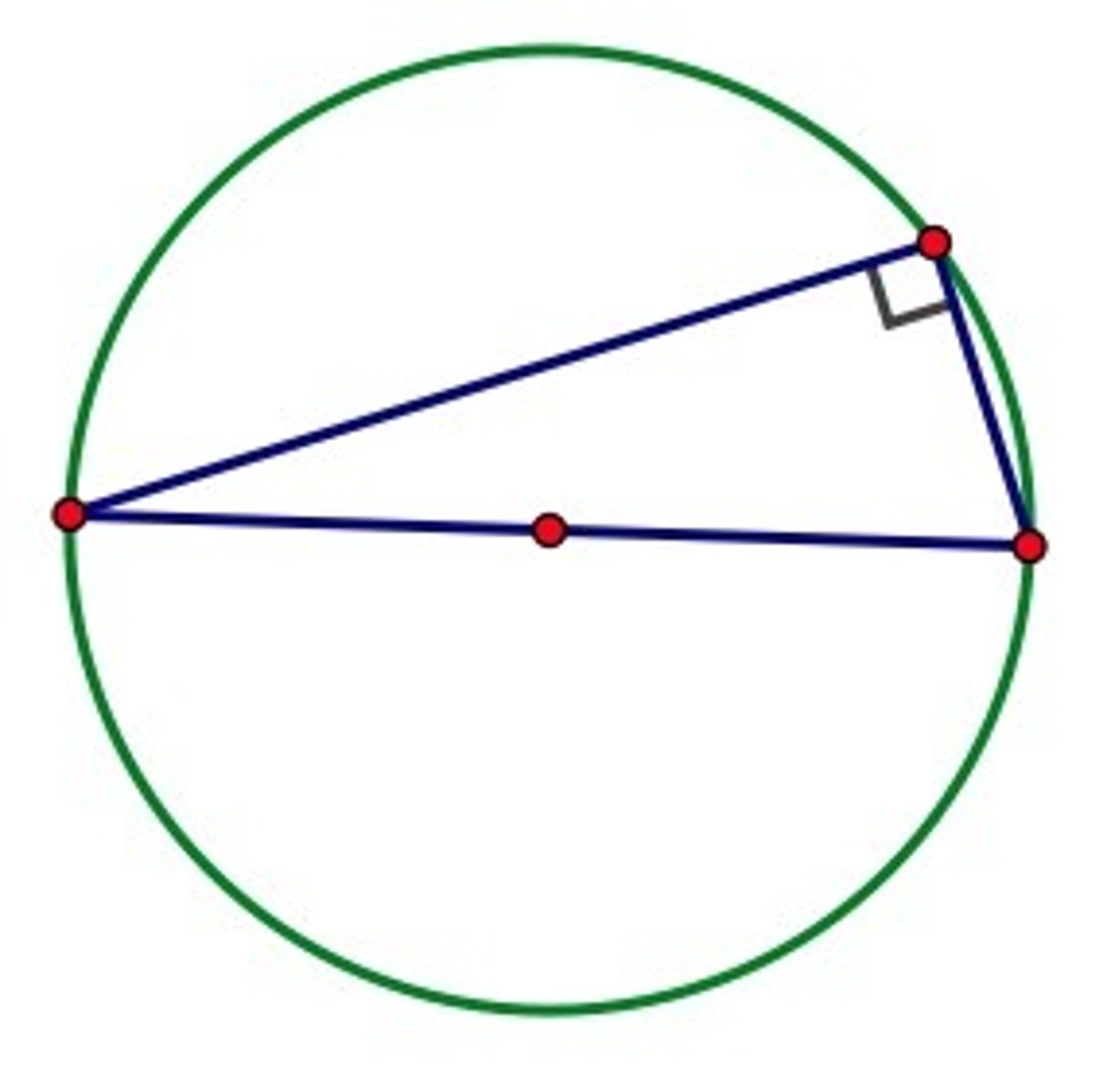
an angle inscribed in a semi circle

is a right angle

base angles of any isosceles shape

are congruent

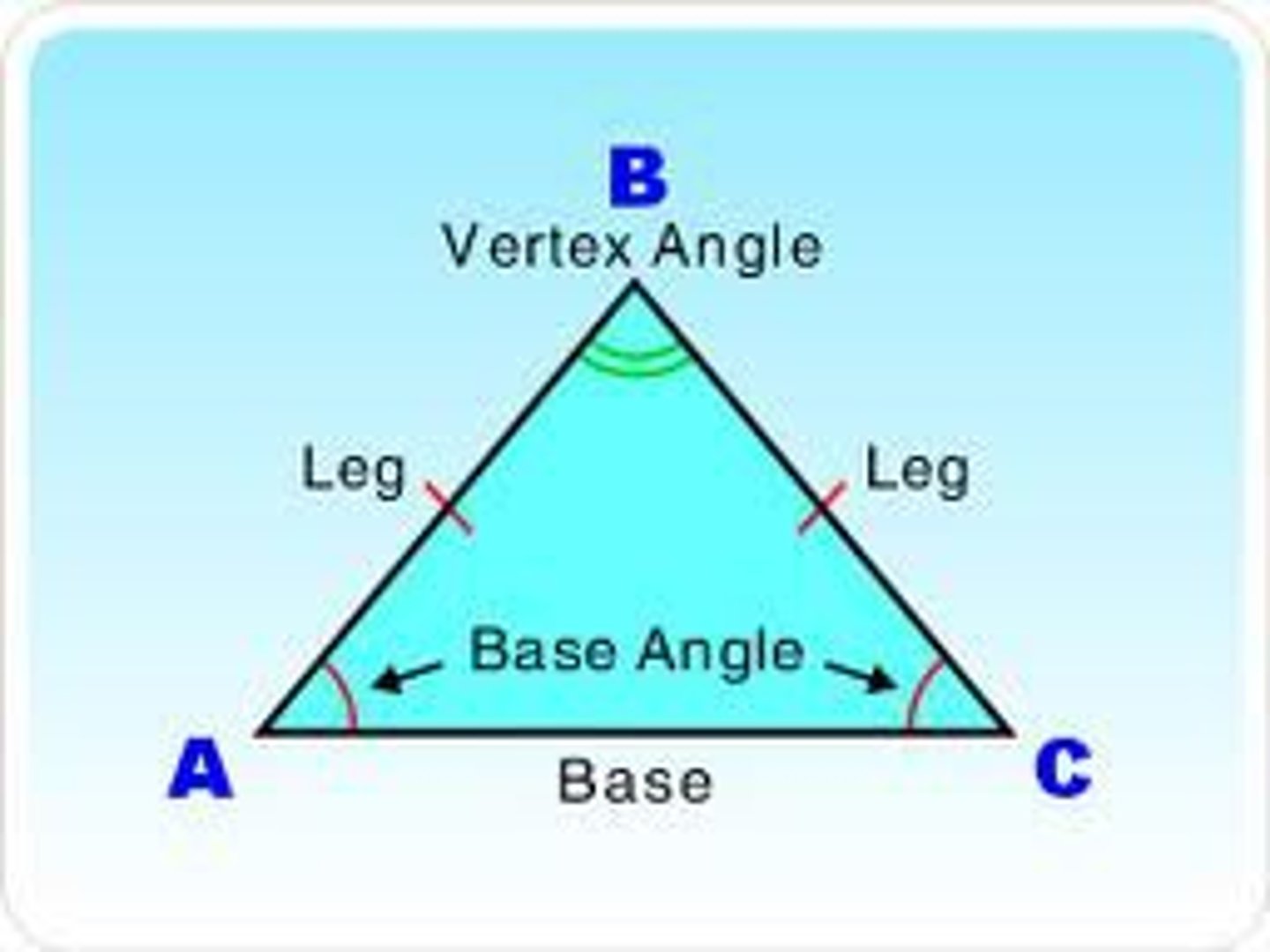
SOH

Sine

Opposite (line segment opposite of the angle)

Hypotenuse (line segment opposite right angle)

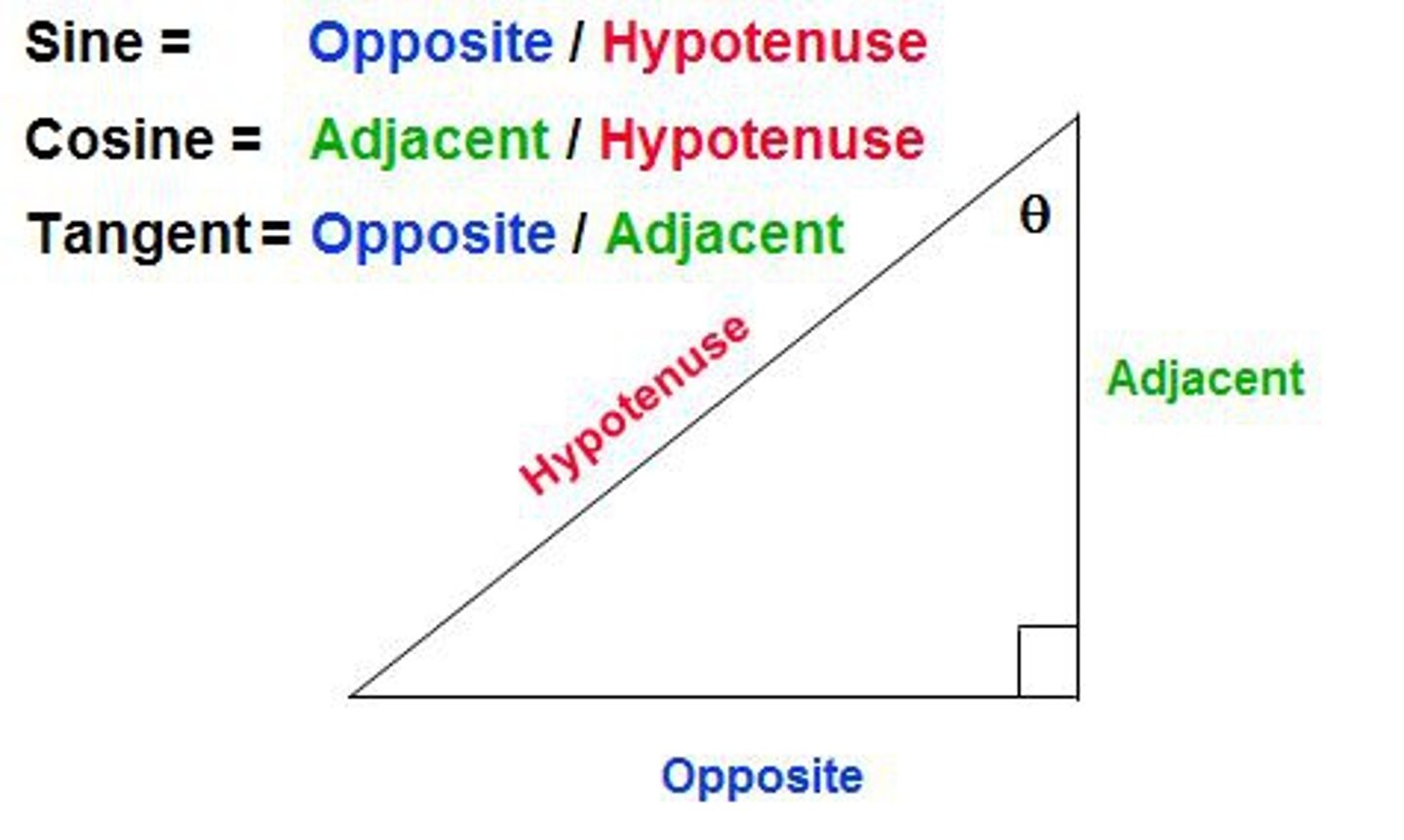
CAH

Cosine

Adjacent (line segment between right angle and angle)

Hypotenuse (line segment opposite right angle)

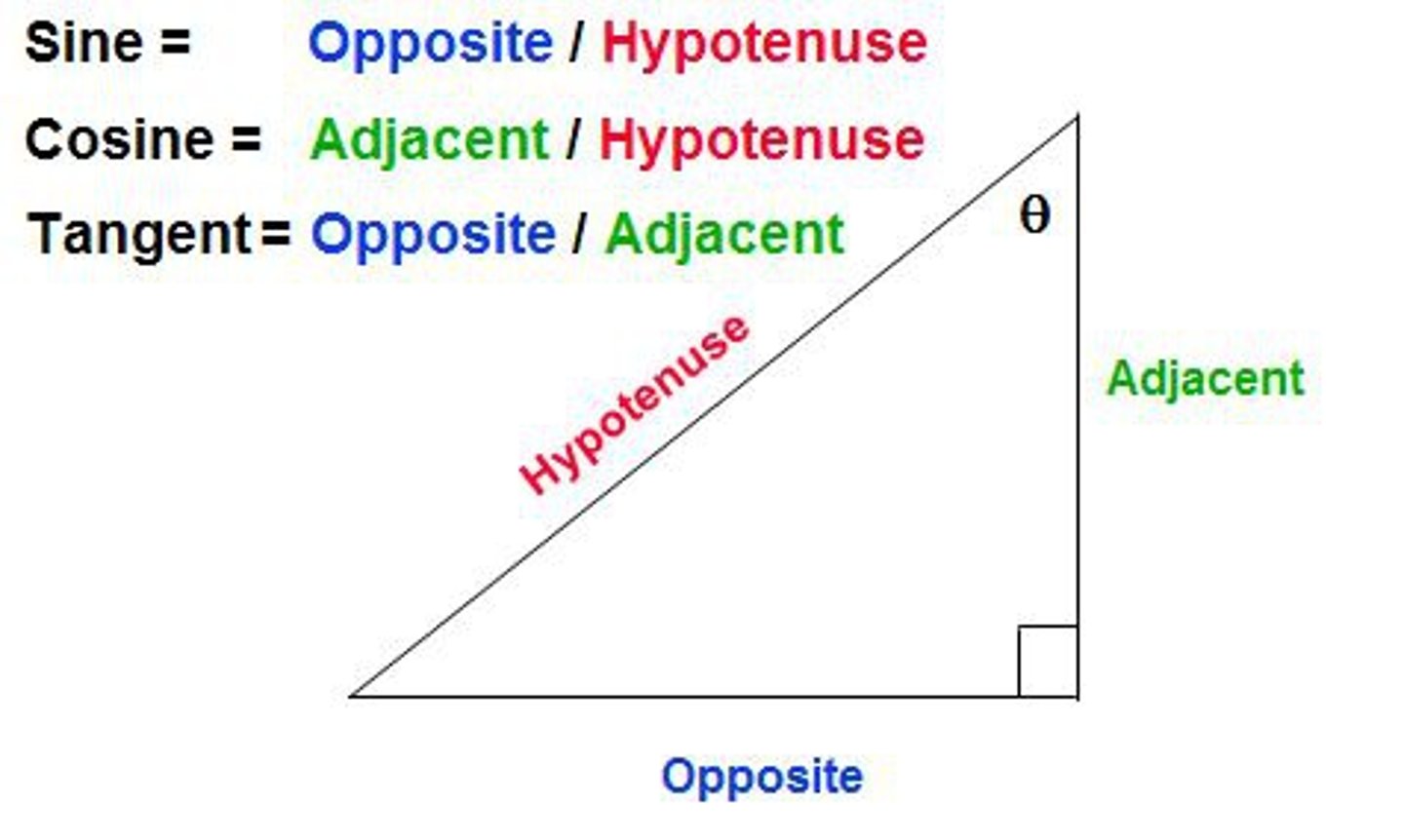
TOA

Tan

Opposite (line segment opposite of the angle)

Adjacent (line segment between right angle and angle)

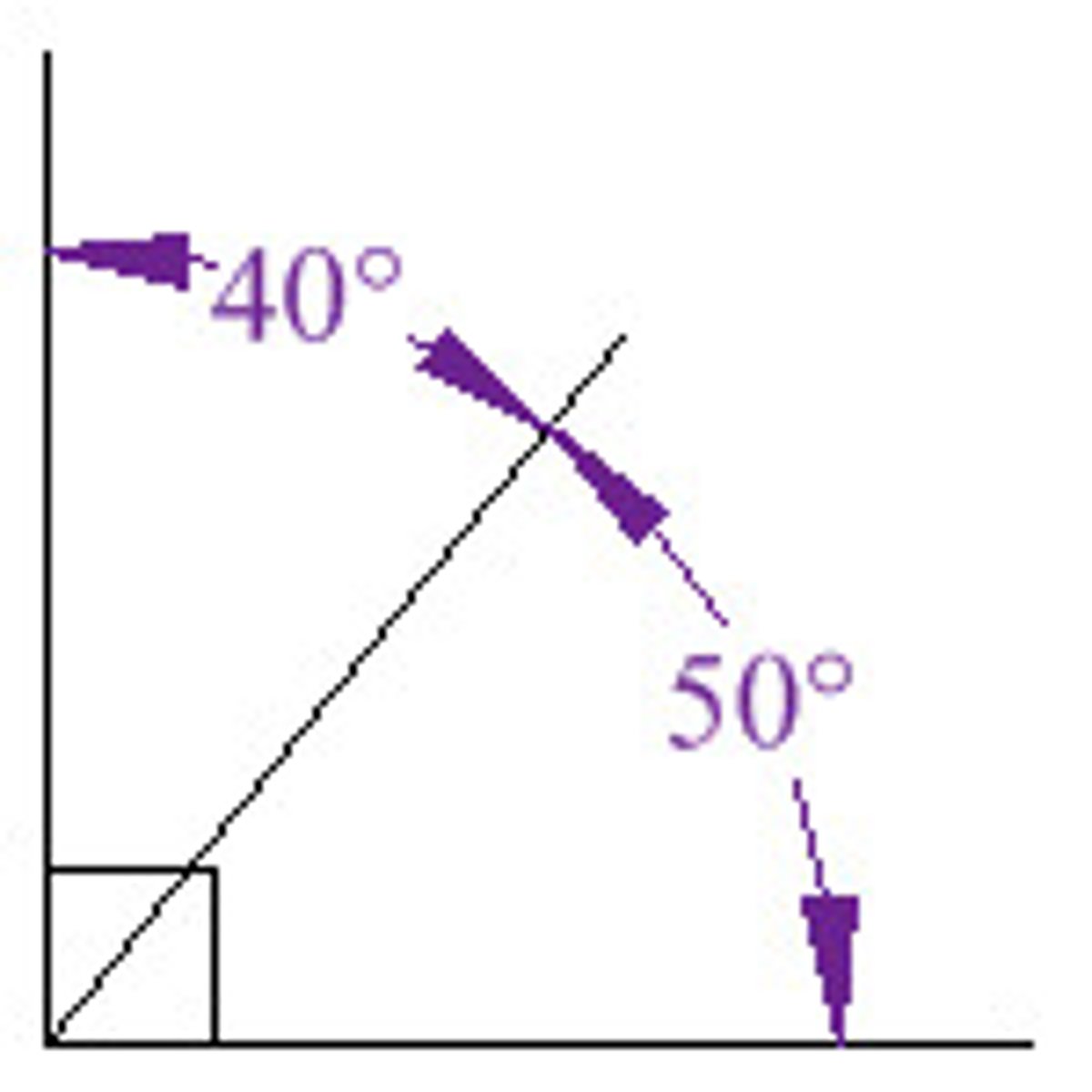
What are complementary angles?

angles that add up to 90 degrees

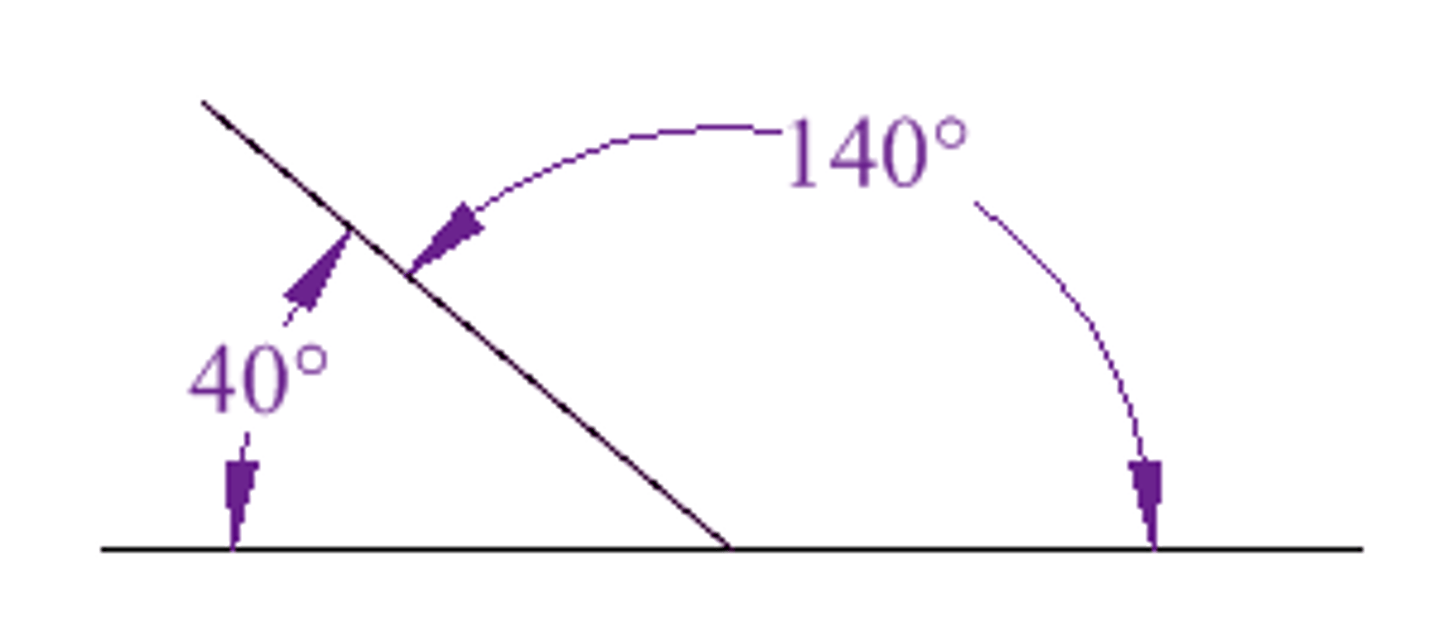
What are supplementary angles?

angles that add up to 180

inscribed angles are always half

of their arc

central angles are always =

to the arc they intercept

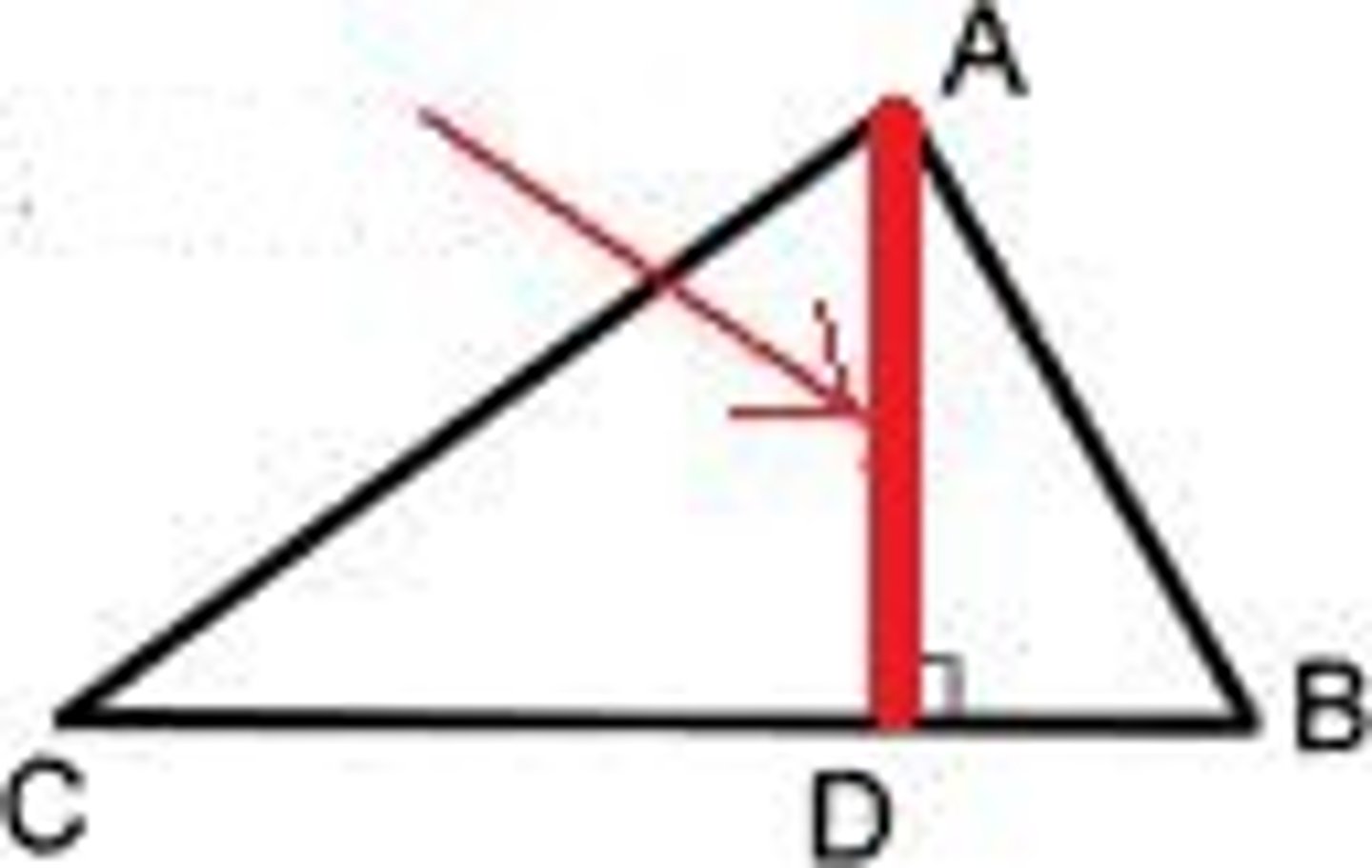
altitude

the length of the perpendicular line from a vertex to the opposite side of a figure. CONCURRENT AT THE ORTHOCENTER

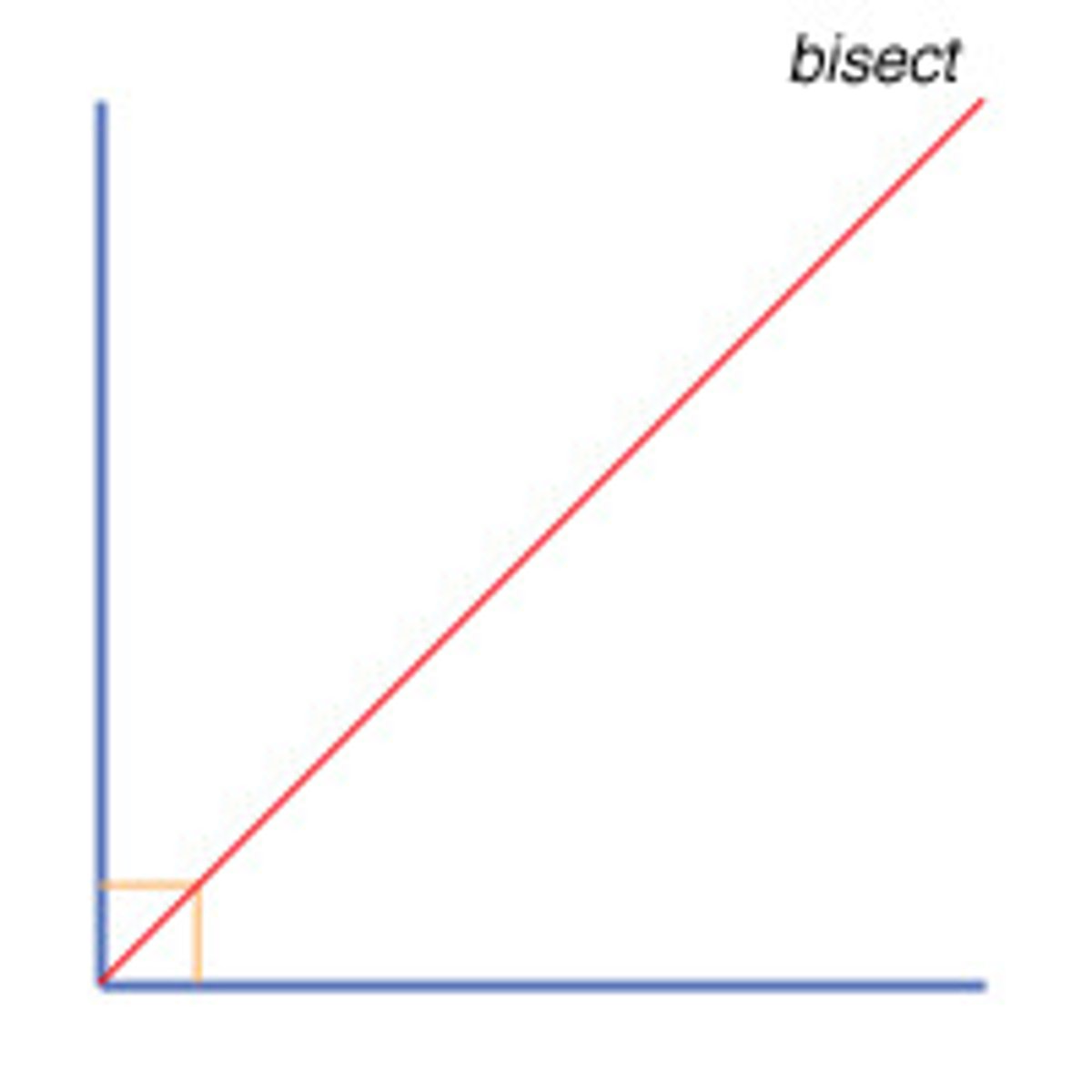
bisect

divide (a line, angle, shape, etc.) into two equal parts.

Reflection y=x

(y,x)

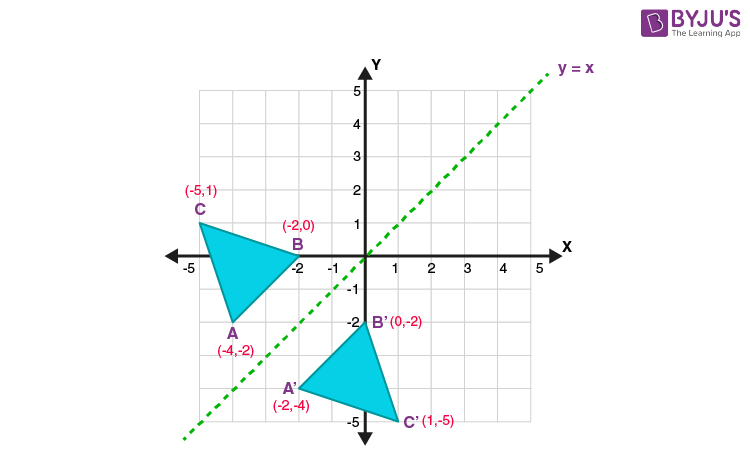
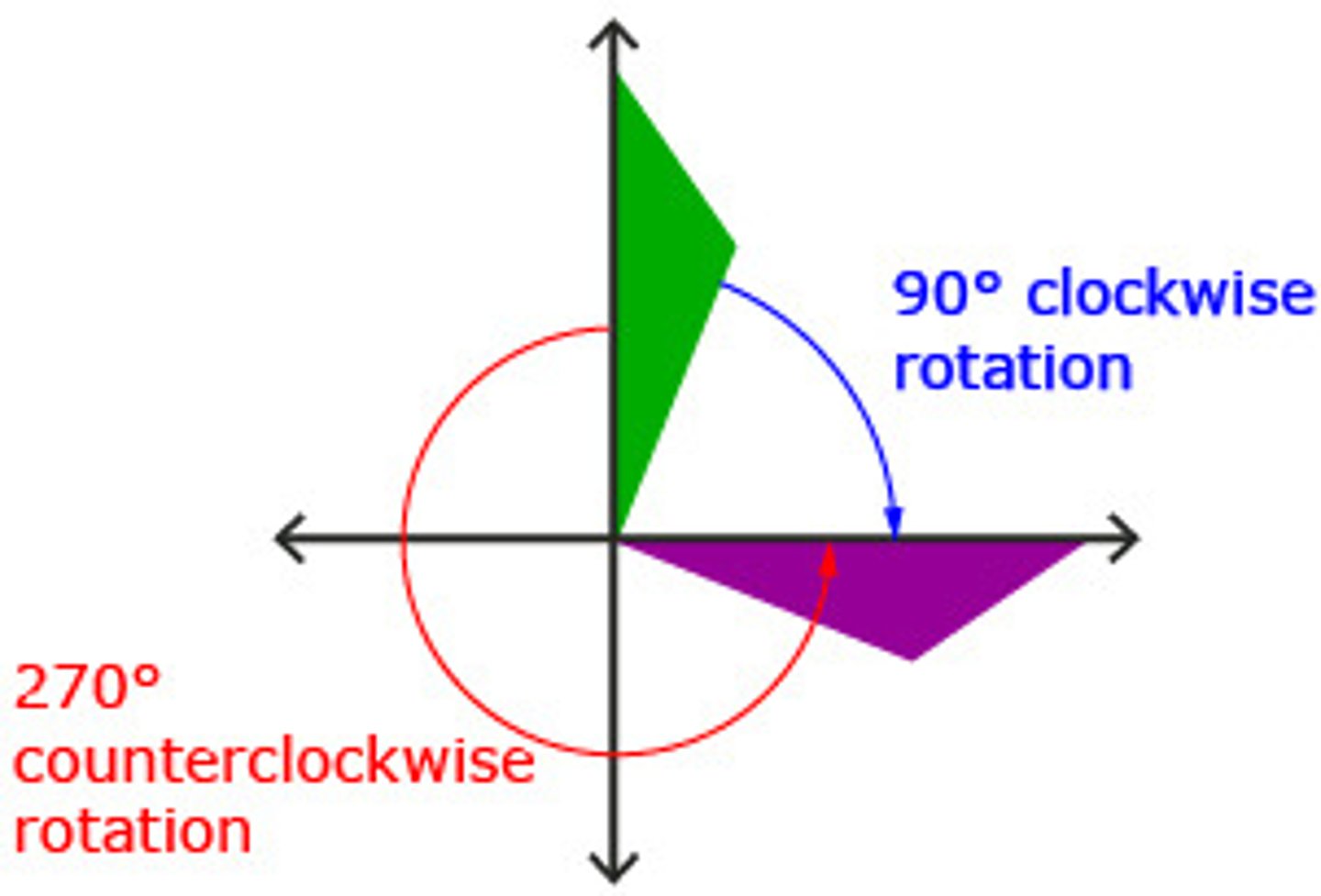
Rotation -90º (x,y)

(y,-x)

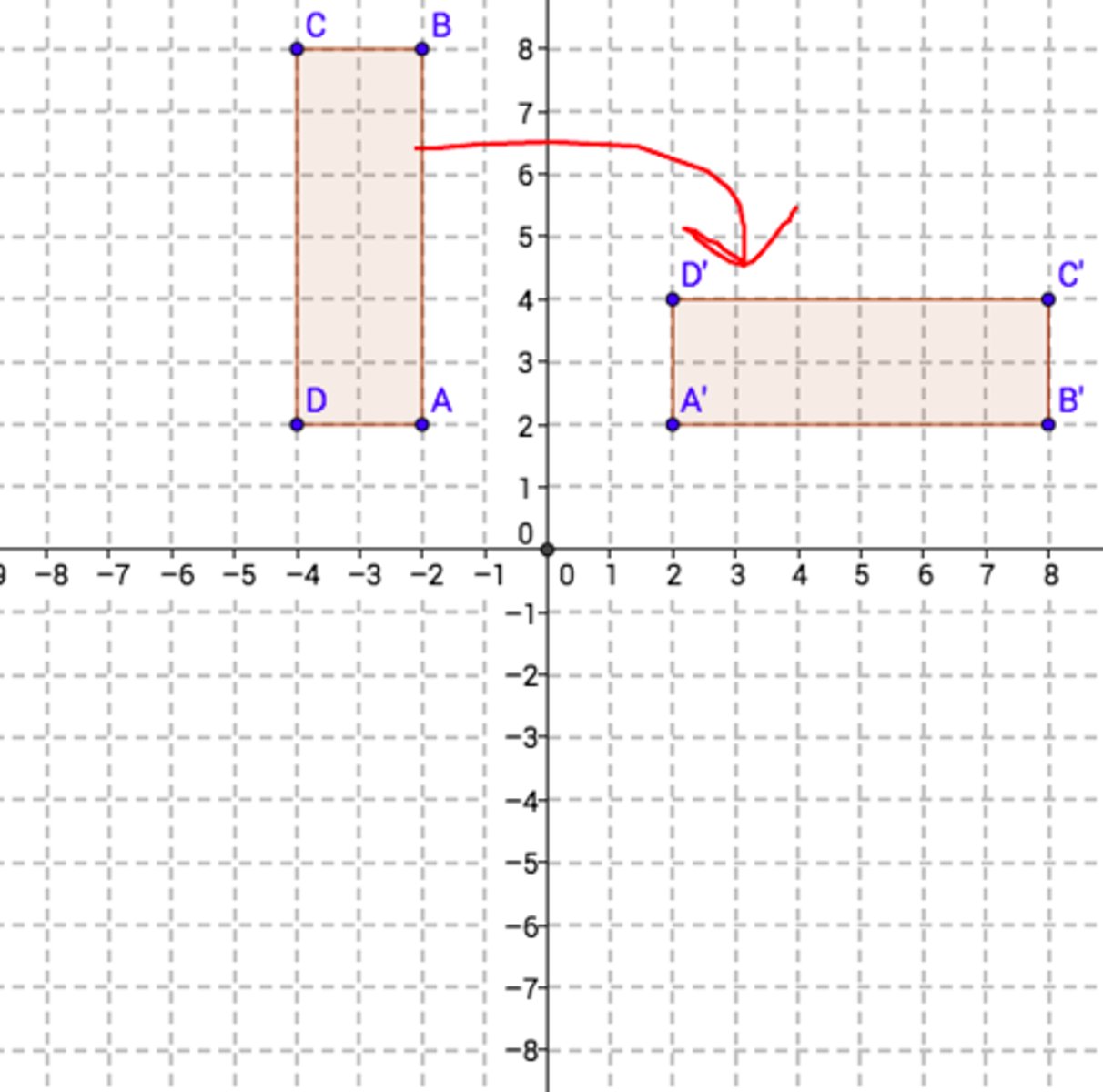
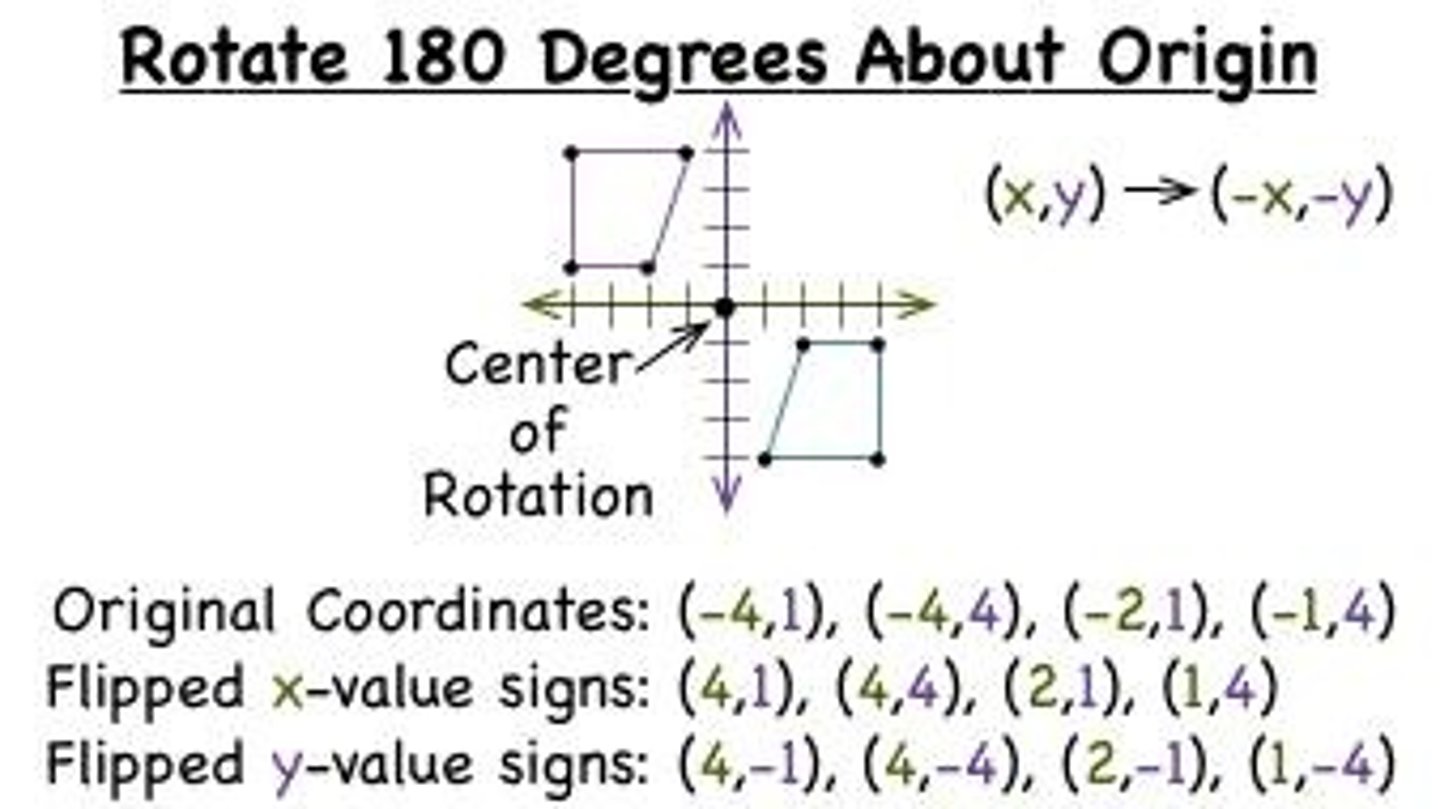
Rotation 180 or -180 (x,y)

(-x,-y)

Reflection ^rx (x,y)

(x,-y) Reflect across the "X"-axis

Reflection ^ry (x,y)

(-x,y) reflect across the y-axis

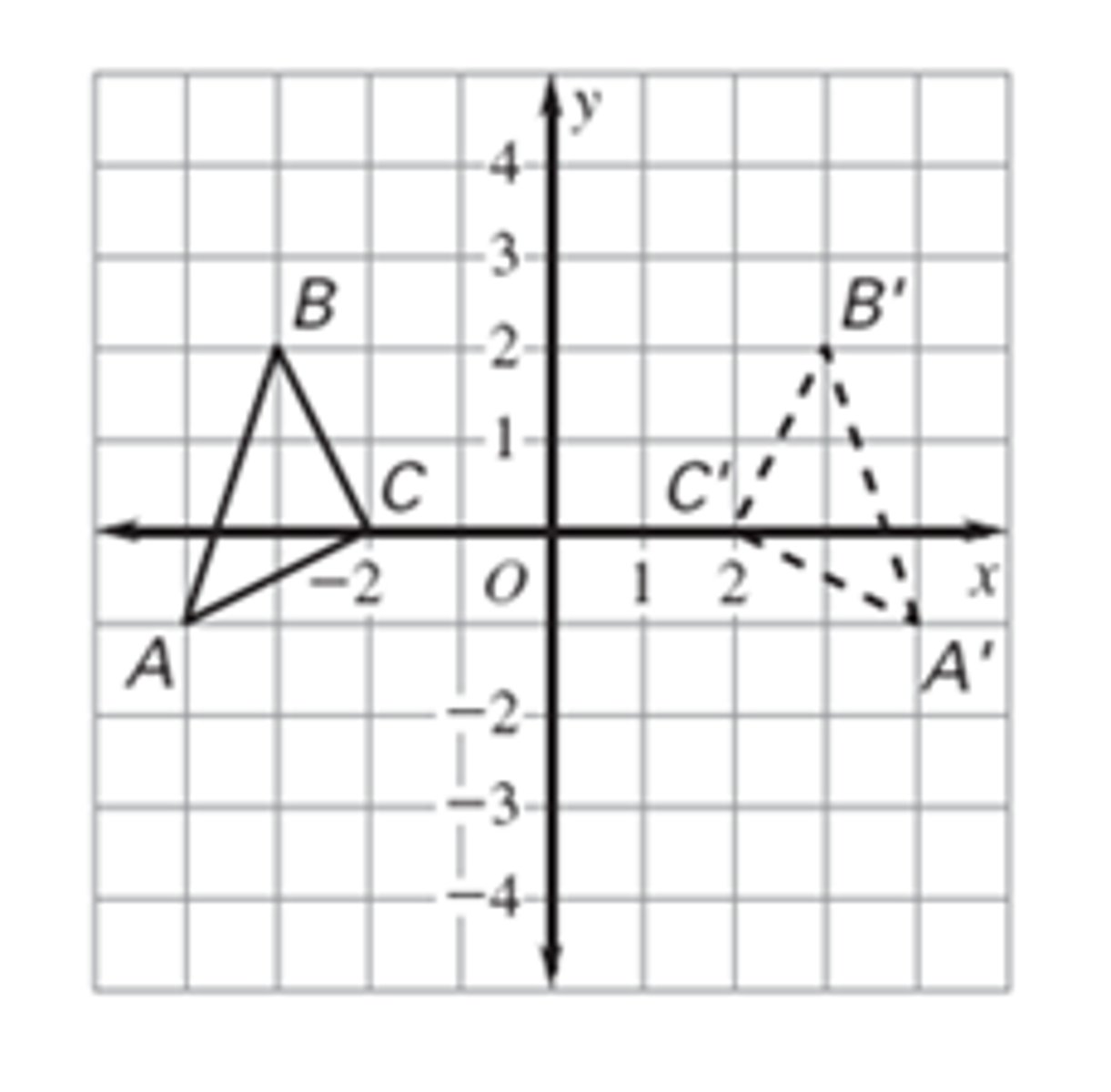
Translation Tab (x,y)

(x+a,y+b) Move it "A" units horizontally and "B" units vertically

Reflection y=-x

(-y,-x)

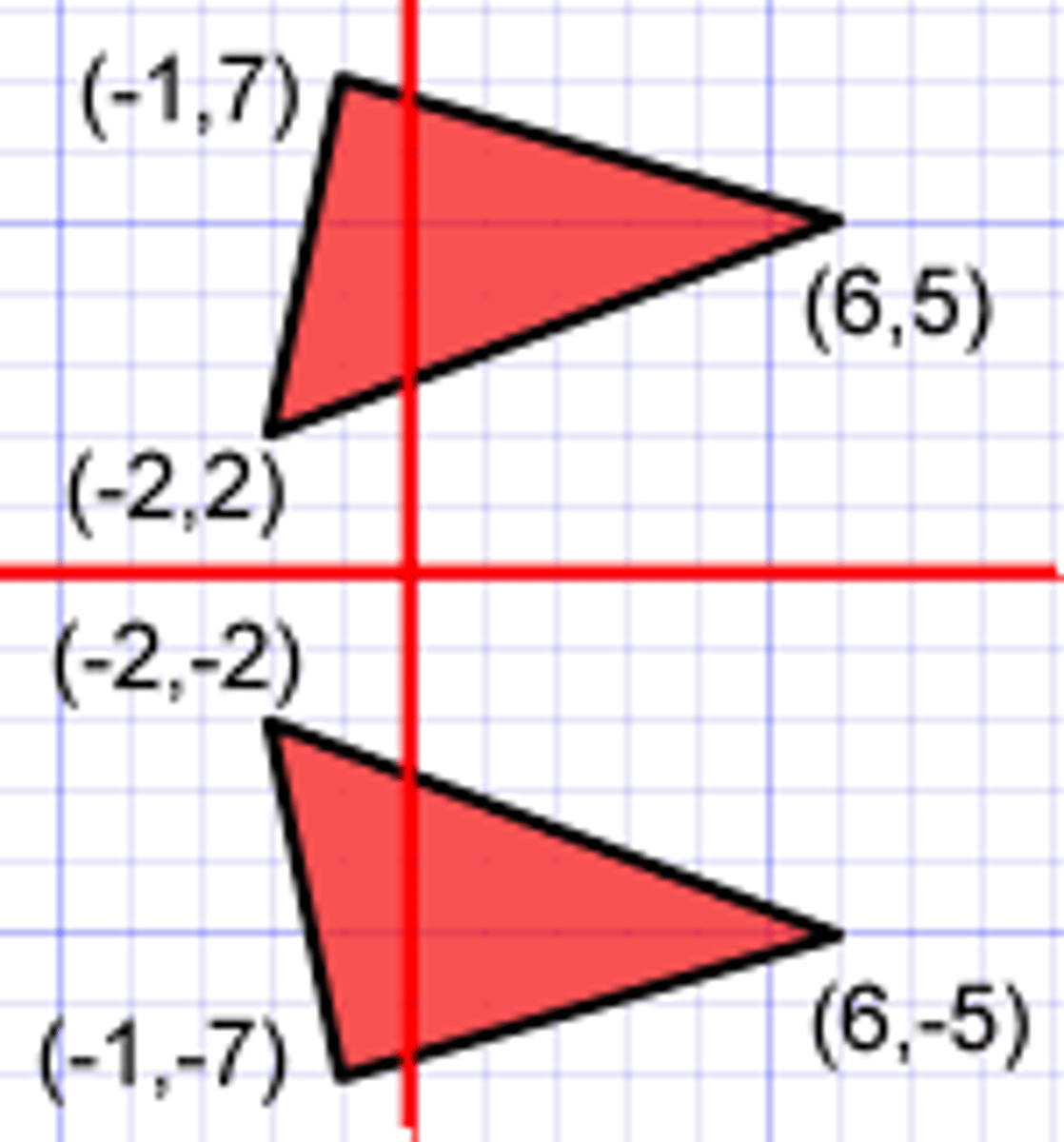
Rotation 90º (x,y)

(-y,x)

line

an infinately long set of points that has no width or thickness

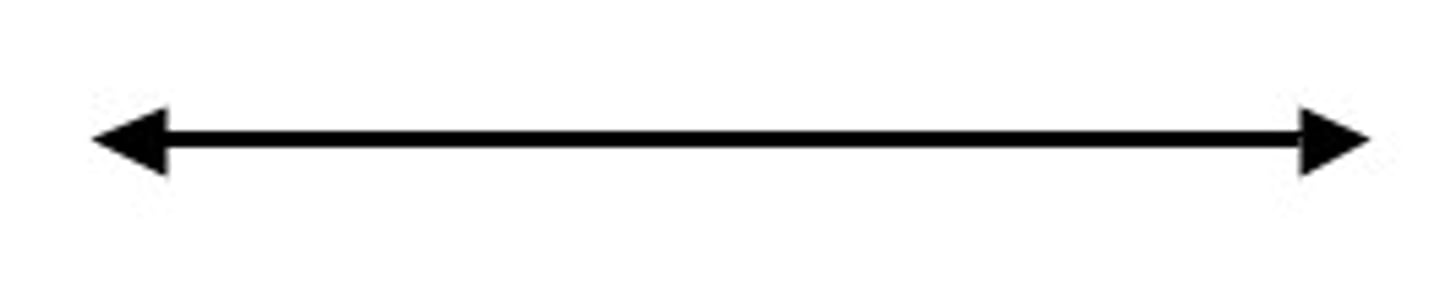
ray

a portion of a line with one end point and including all points on one side of the end point

segment

a portion of a line bounded by two end points

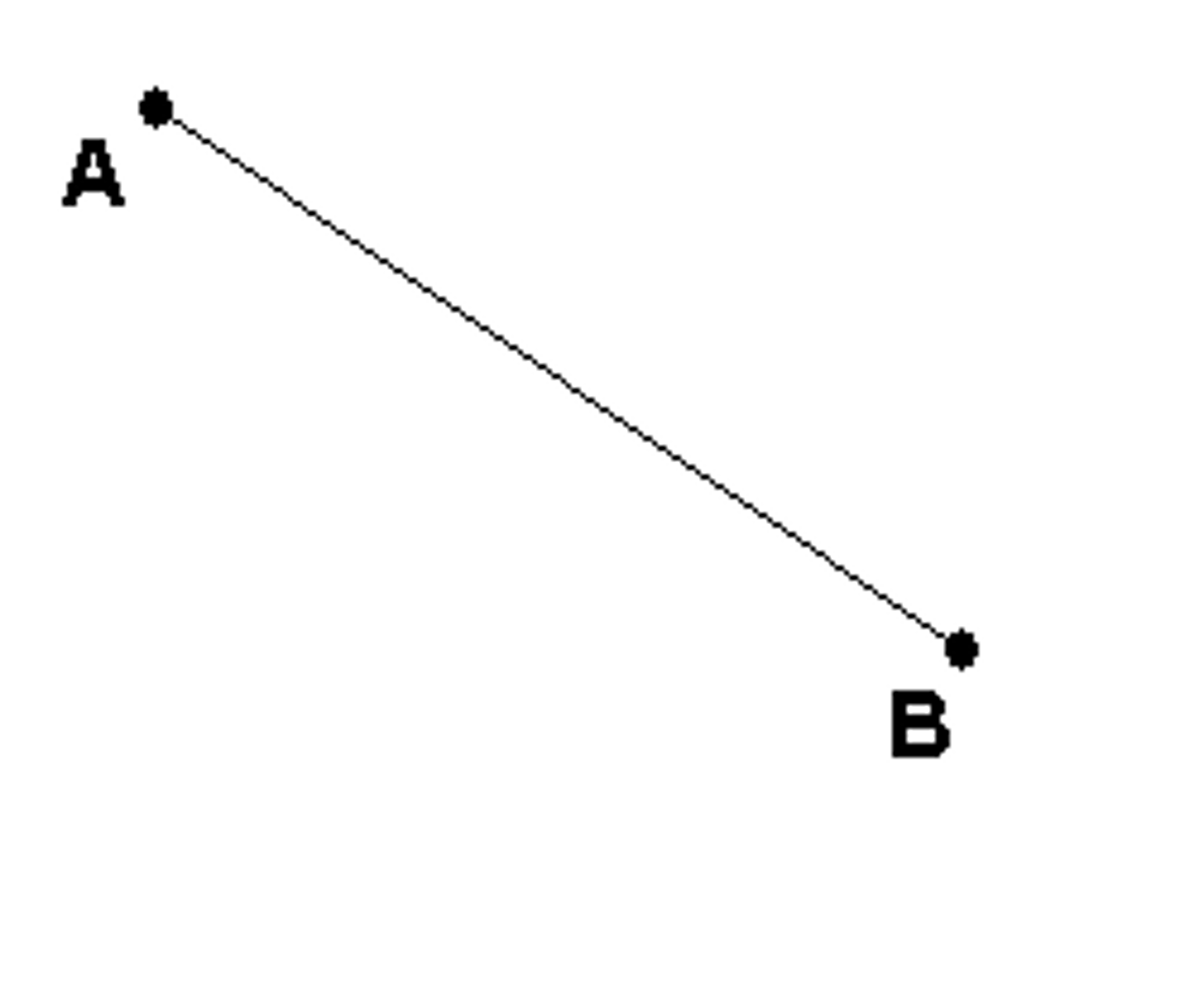
plane

a flat set of points with no thickness that extends infinatelely in all directions

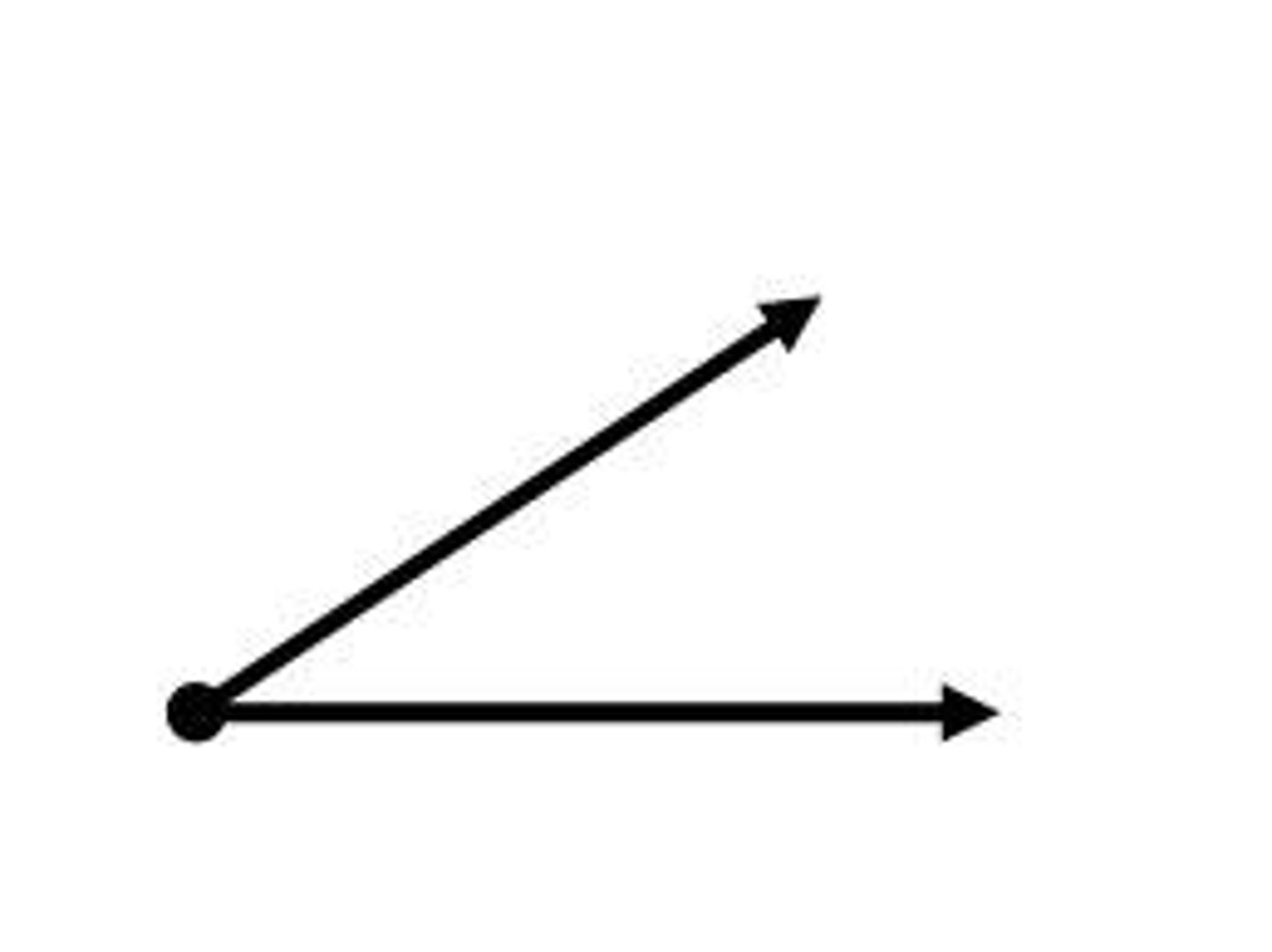
angle

a figure formed by two rays with a common endpoint

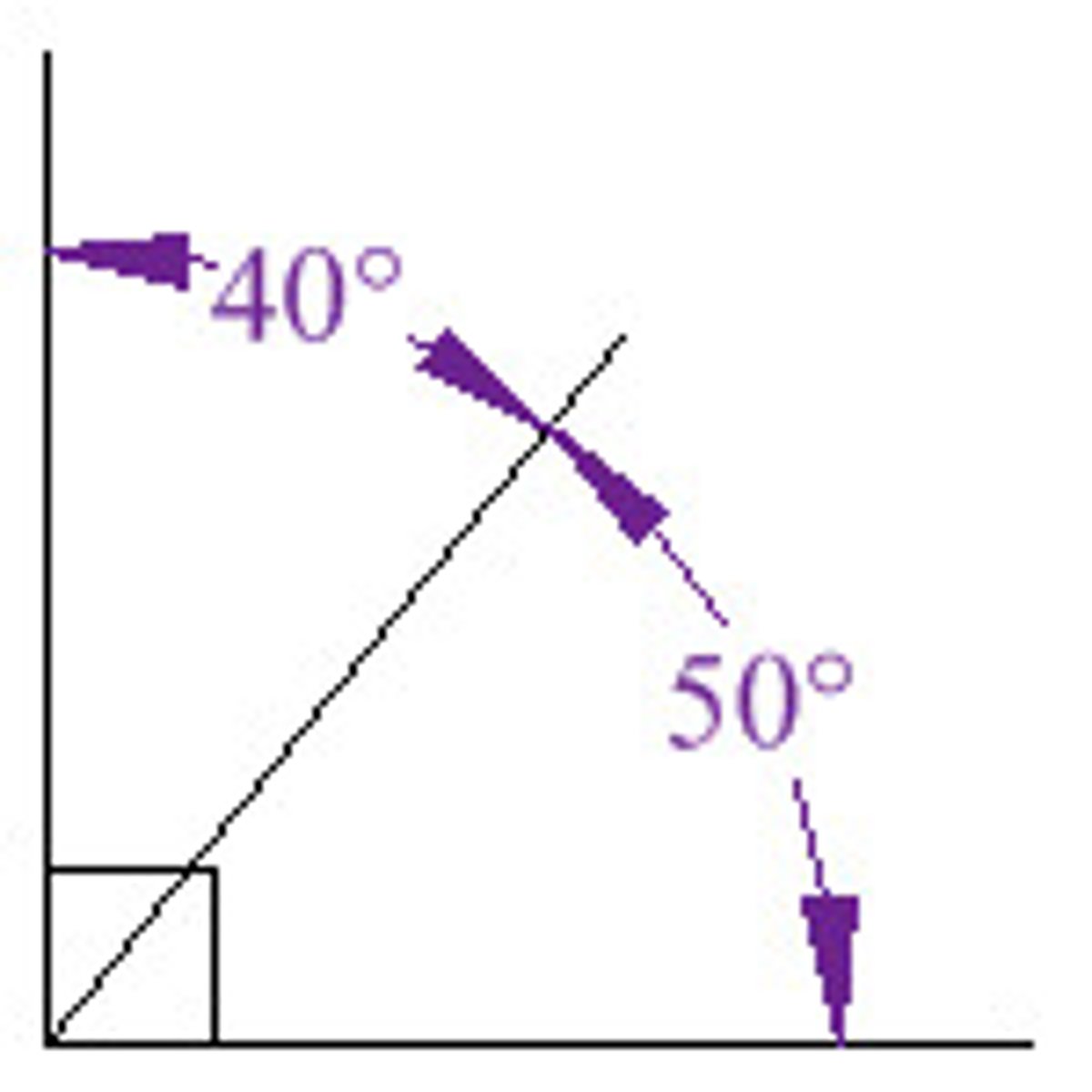
angle measure

the opening of an angle, measured in degrees or radians

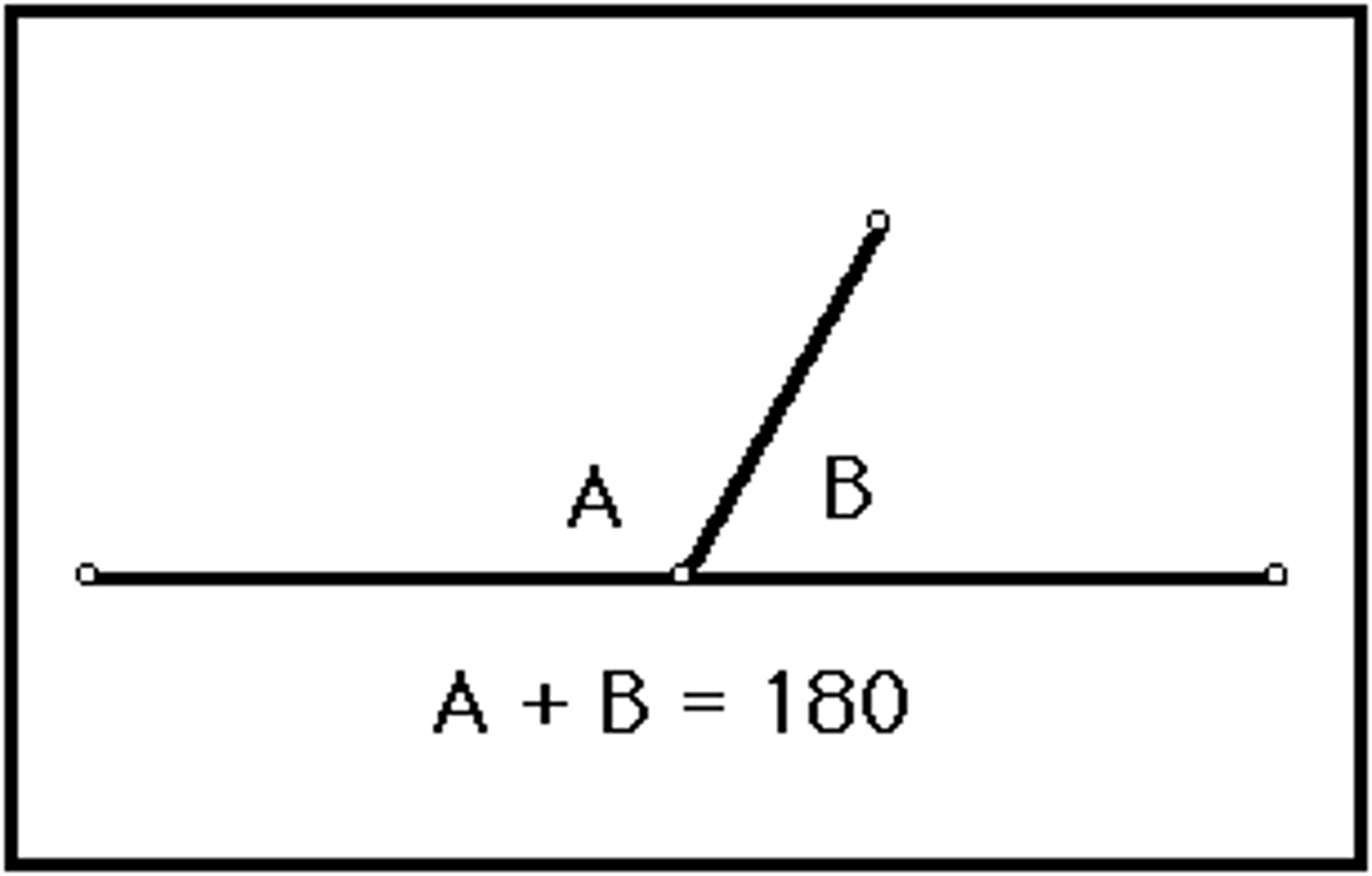
linear pair

two adjacent angles that form a straight line (180º line)

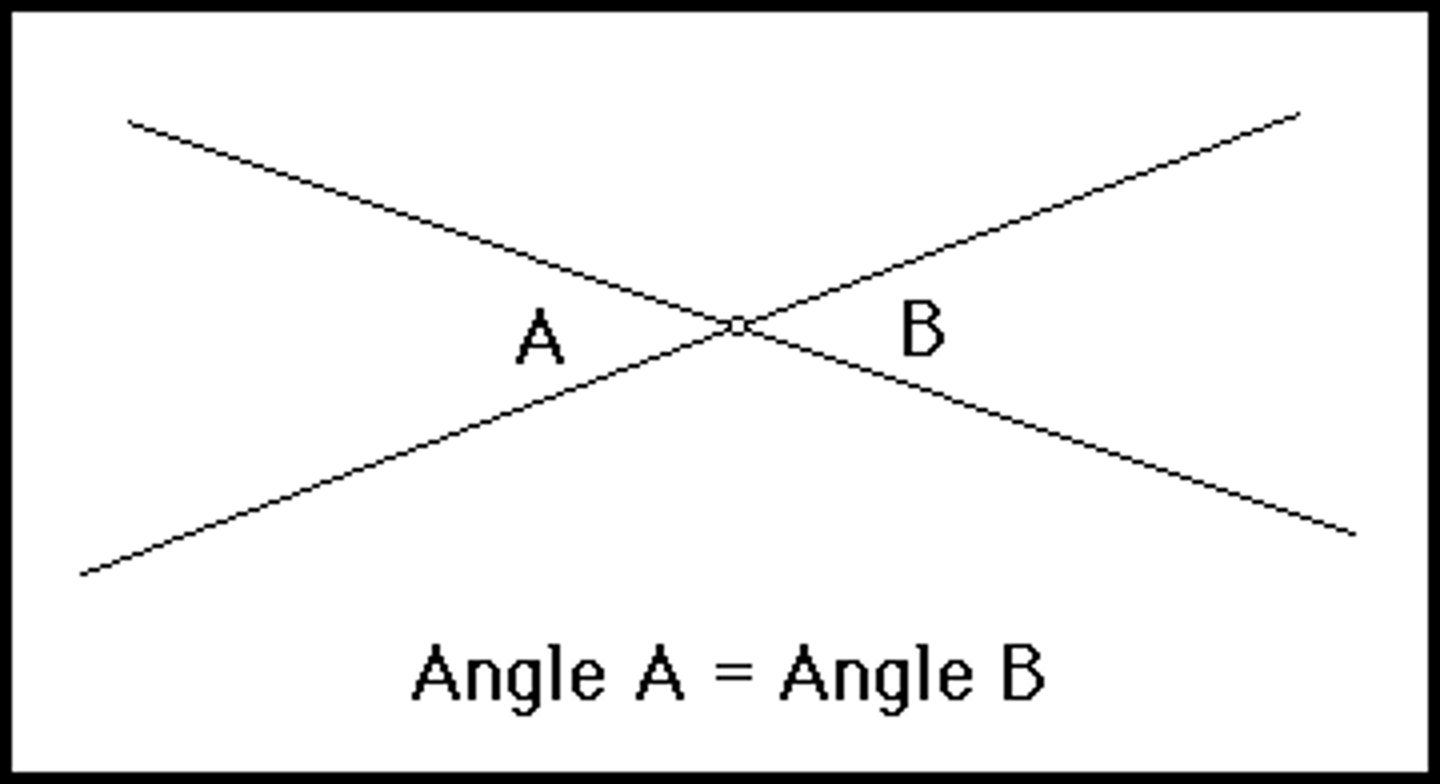
vertical angles

the congruent opposite angles formed by intersecting lines

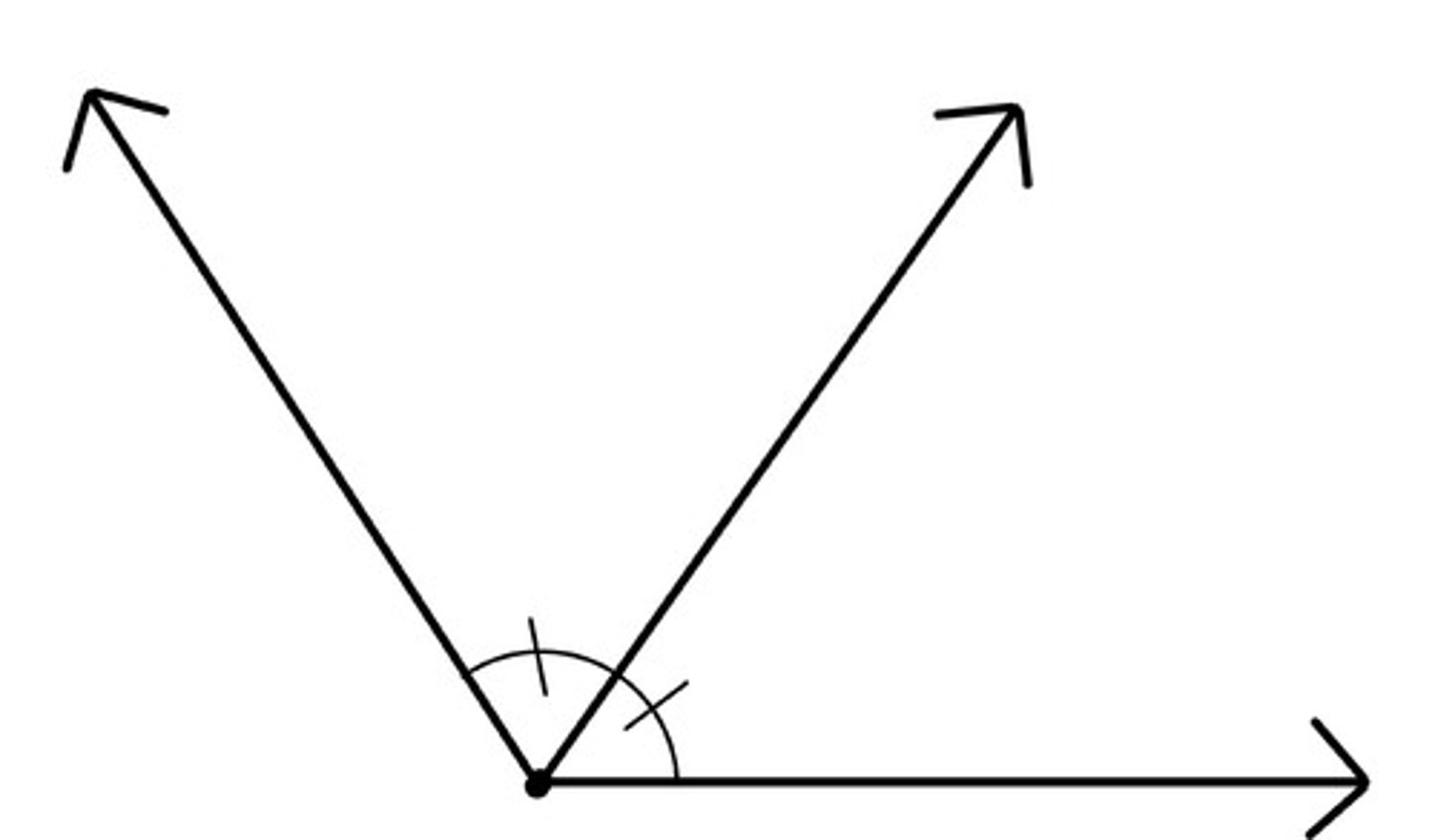
angle bisectors

divide angles into two congruent angles. CONCURRANT AT THE INCENTER

alternate interior angles

are congruent

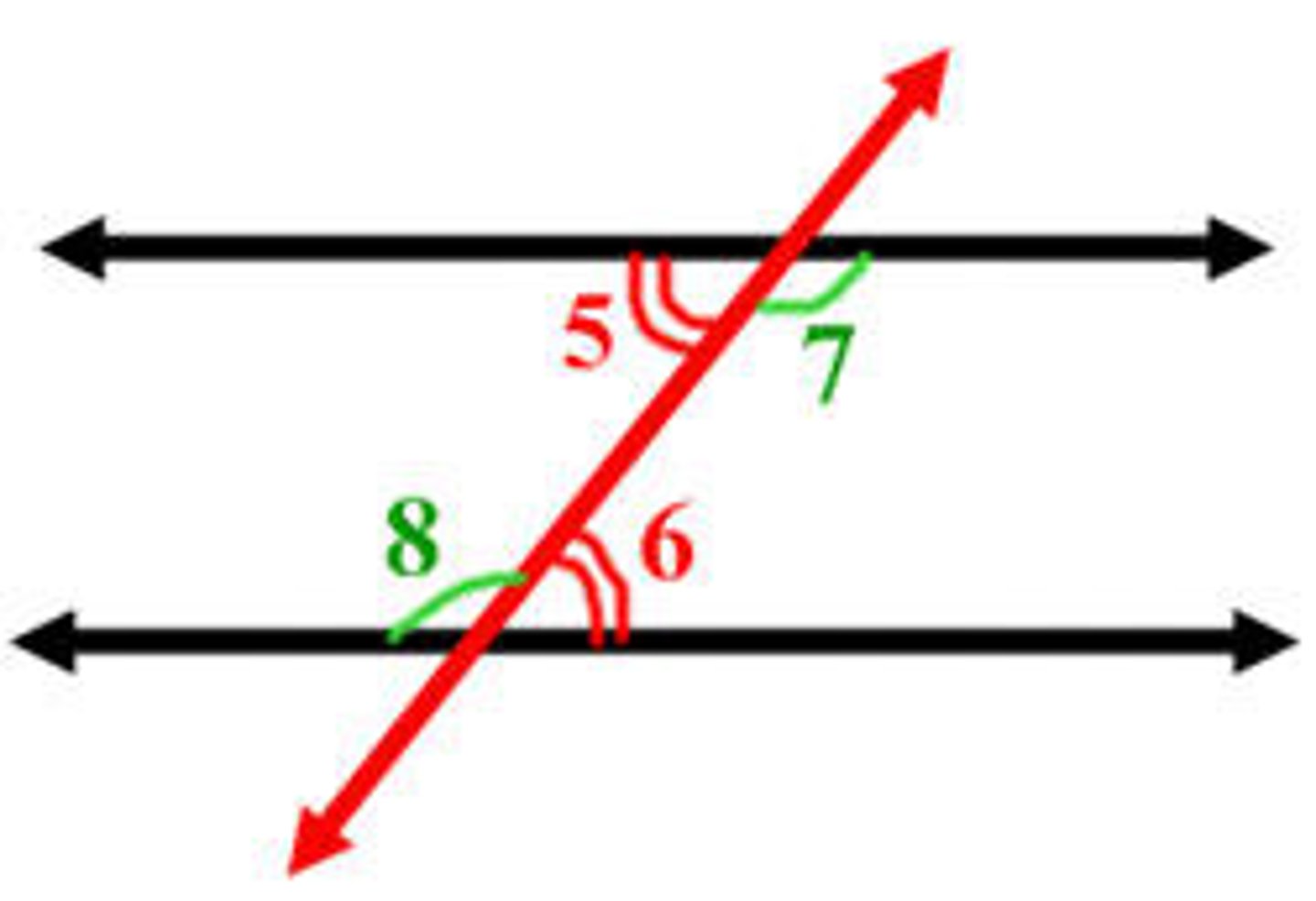
same side interior angles

are supplementary

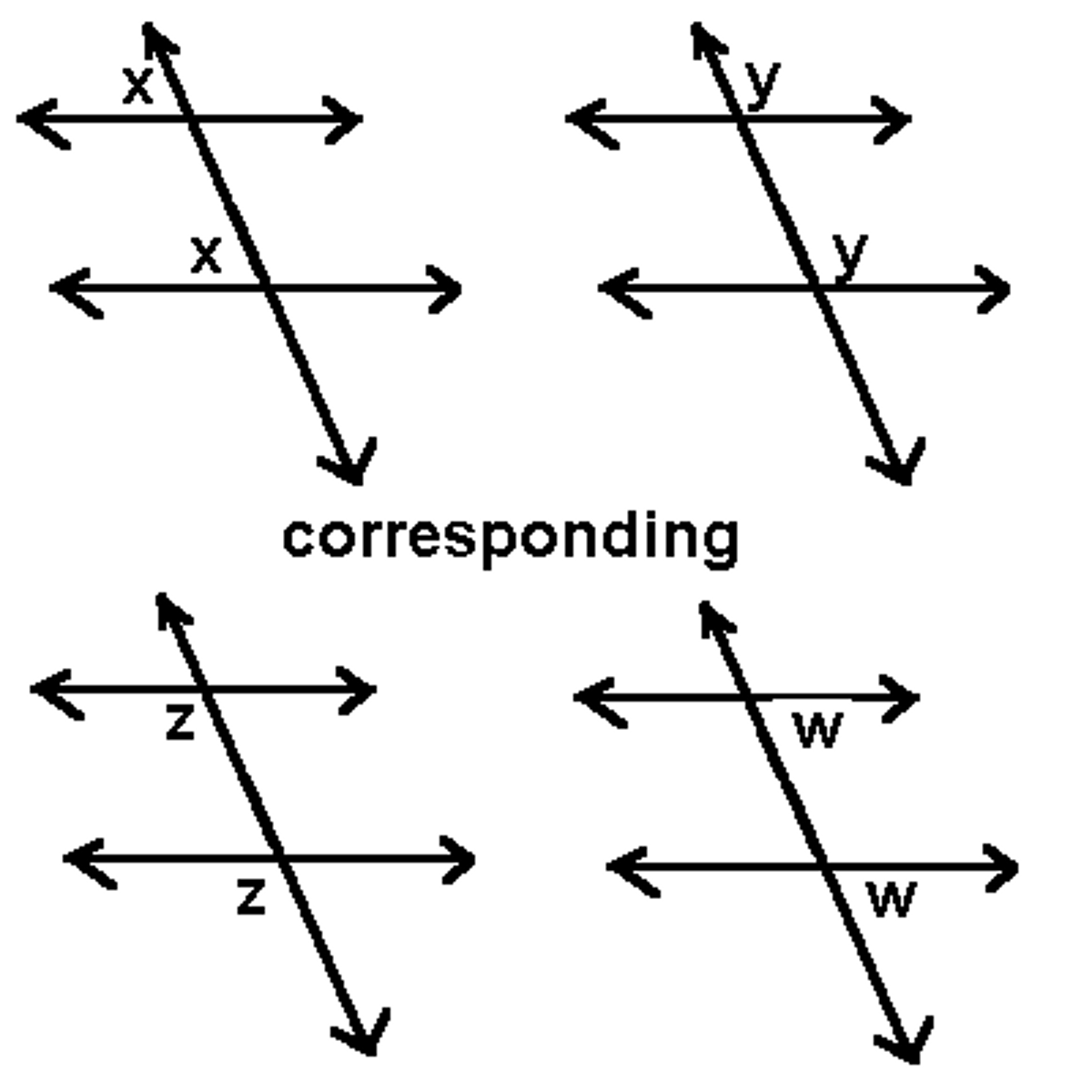
corresponding angles

are congruent

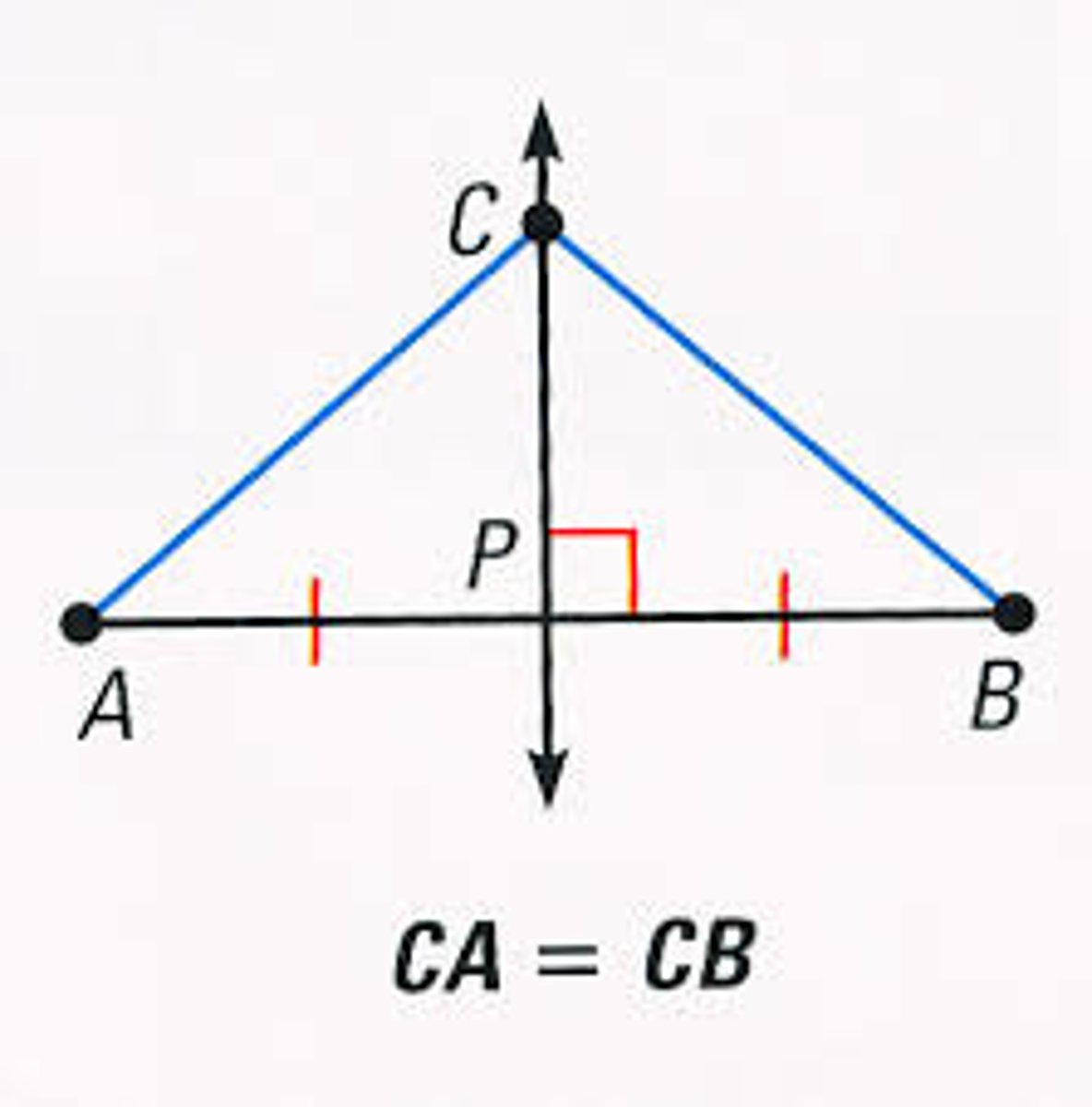
perpendicular bisector

a line, segment, or ray that is perpendicular to and bisects a segment. CONCURRENT AT THE CIRCUMCENTER

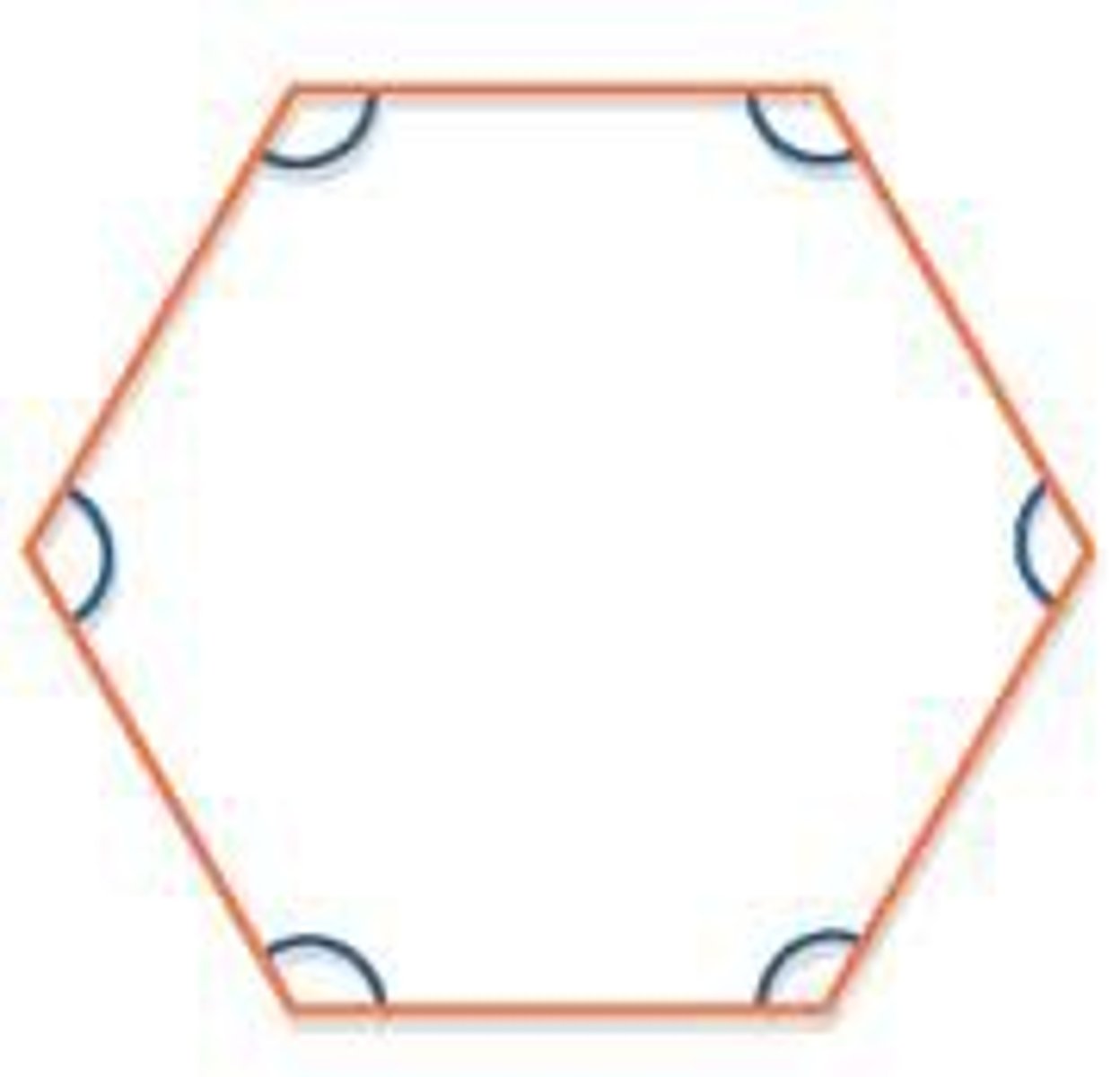
interior angle (of a polygon)

the angle inside the polygon formed by two adjacent sides

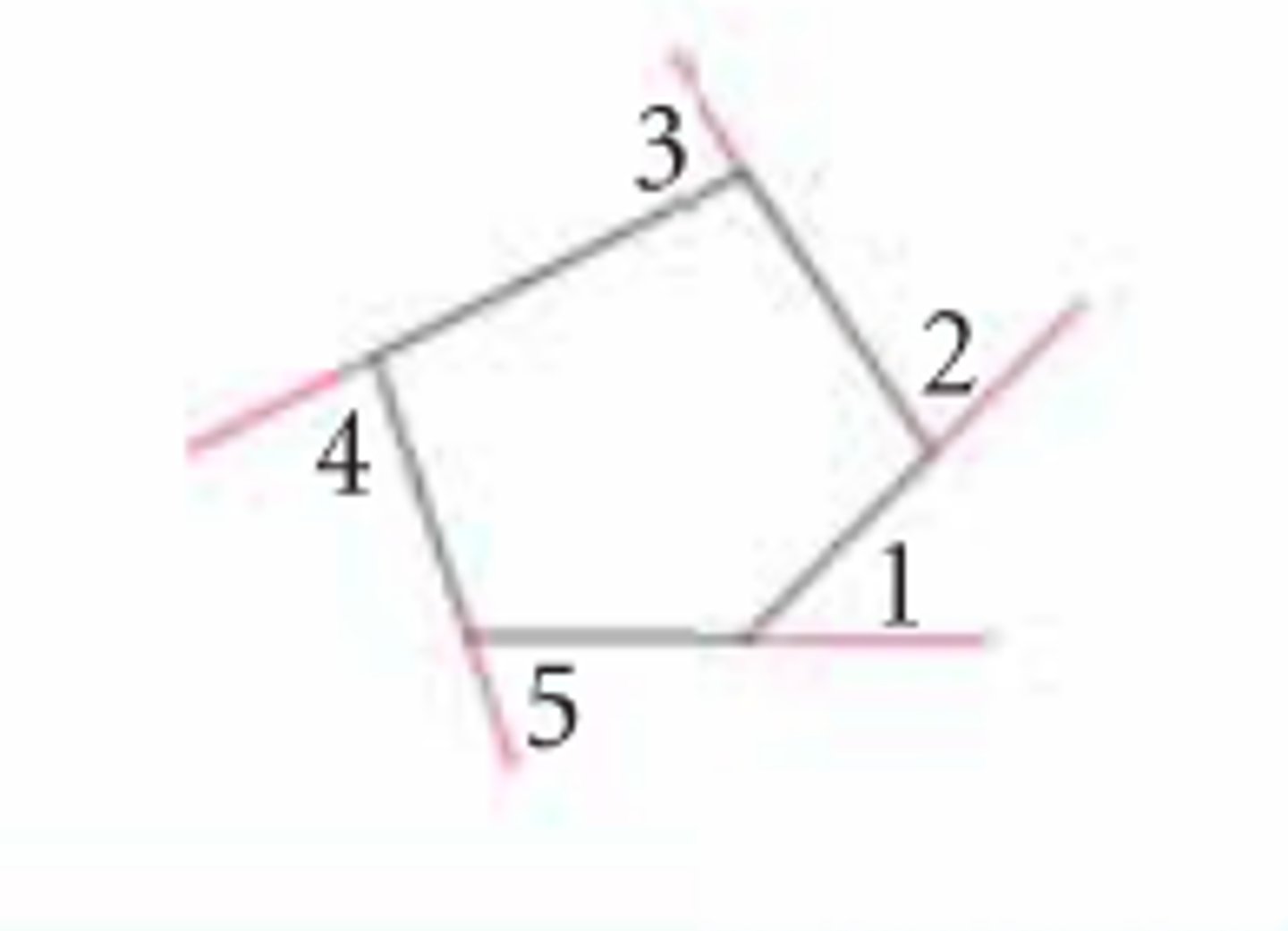
exterior angle (of a polygon)

the angle formed by a side and the extension of an adjacent side in a polygon

two examples of transformations that are neither rigid motions nor similarity transformations:e

horizontal stretch and vertical stretch

Horizontal stretch

elongates the figure only in the horizontal direction. On the coordinate plane, the x-coordinate of every point will be multiplied by a scale factor

Vertical stretch

elongates the figure only in the vertical direction. On the coordinate plane, the y-coordinate of every point will be multiplied by a scale factor

median

a segment from the vertex to the midpoint of th opposite side. CONCURRNT AT THE CENTROID

scalene triangles

no sides are congruent

isosceles

two legs and base angles are congruent

equilateral

three sides are congruent

All Of My Children Are Bringing In Peanut Butter Cookies

Altitudes/orthocenter. Medians/centroid. Angle bisectors/incenter. Perpindicular bisectors/circumcenter

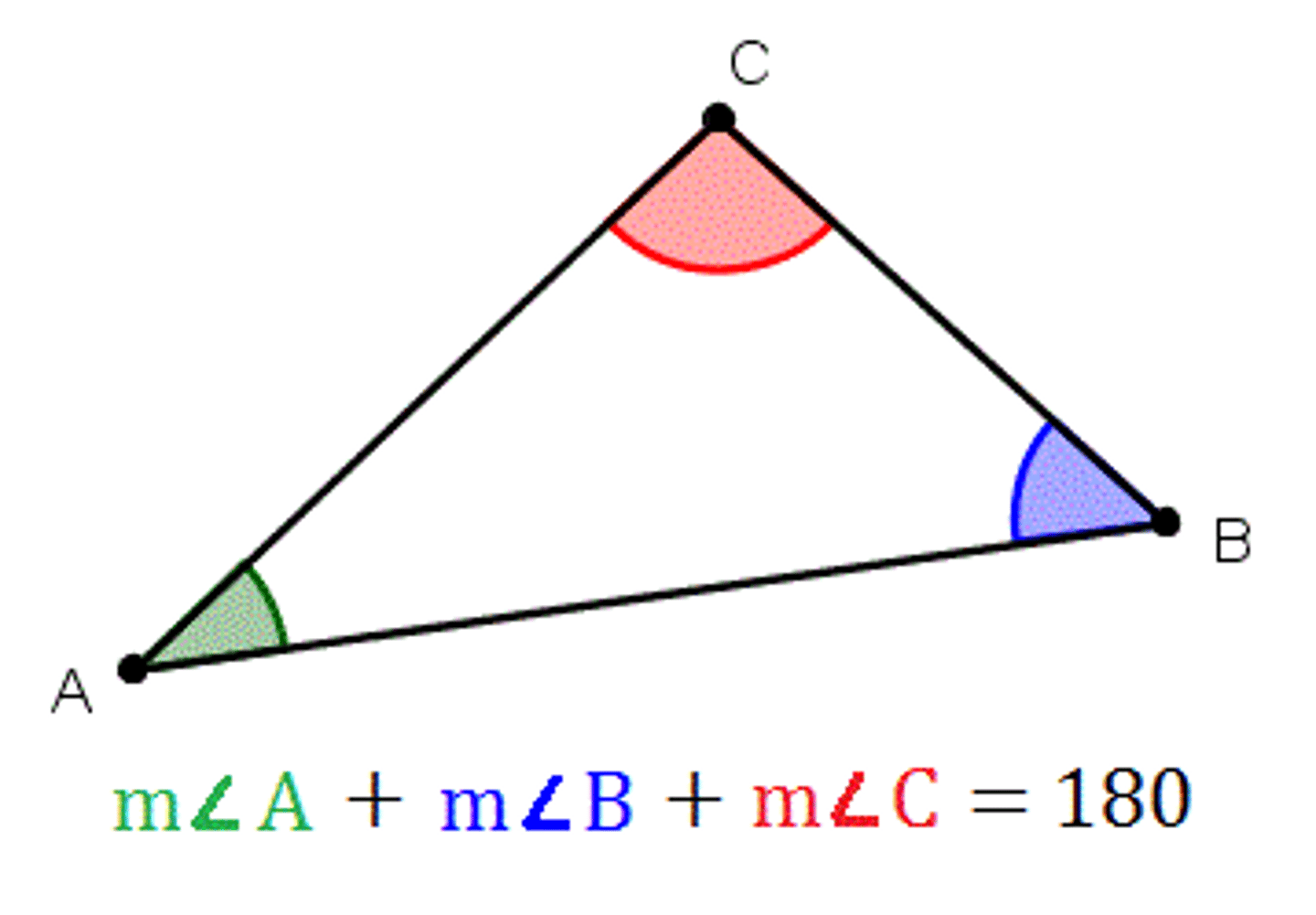
Angle sum theorem

the sum of the measures of the interior angles = 180º

exterior angle theorem

the measure of any exterior angle of a triangle = the sum of the measures of the nonadjacent interior angles

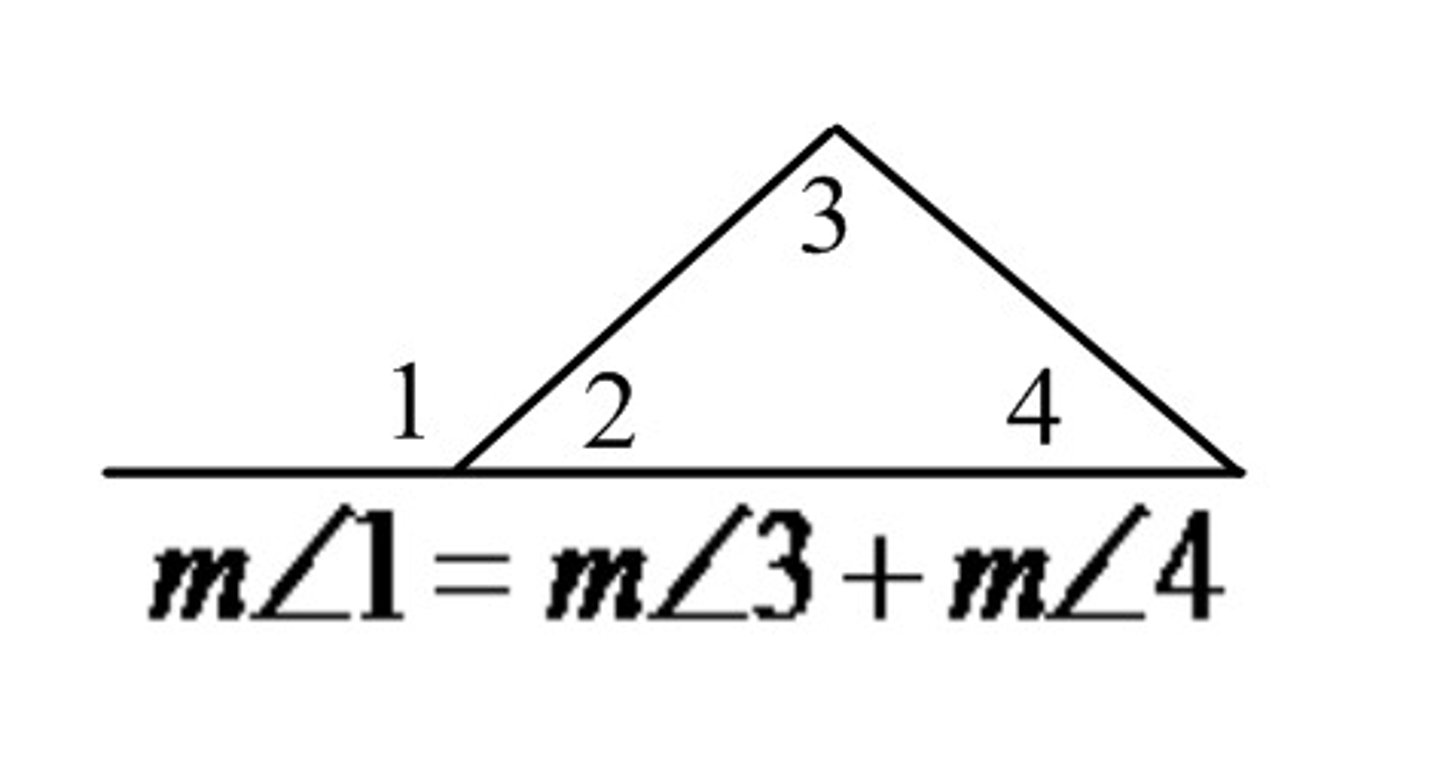
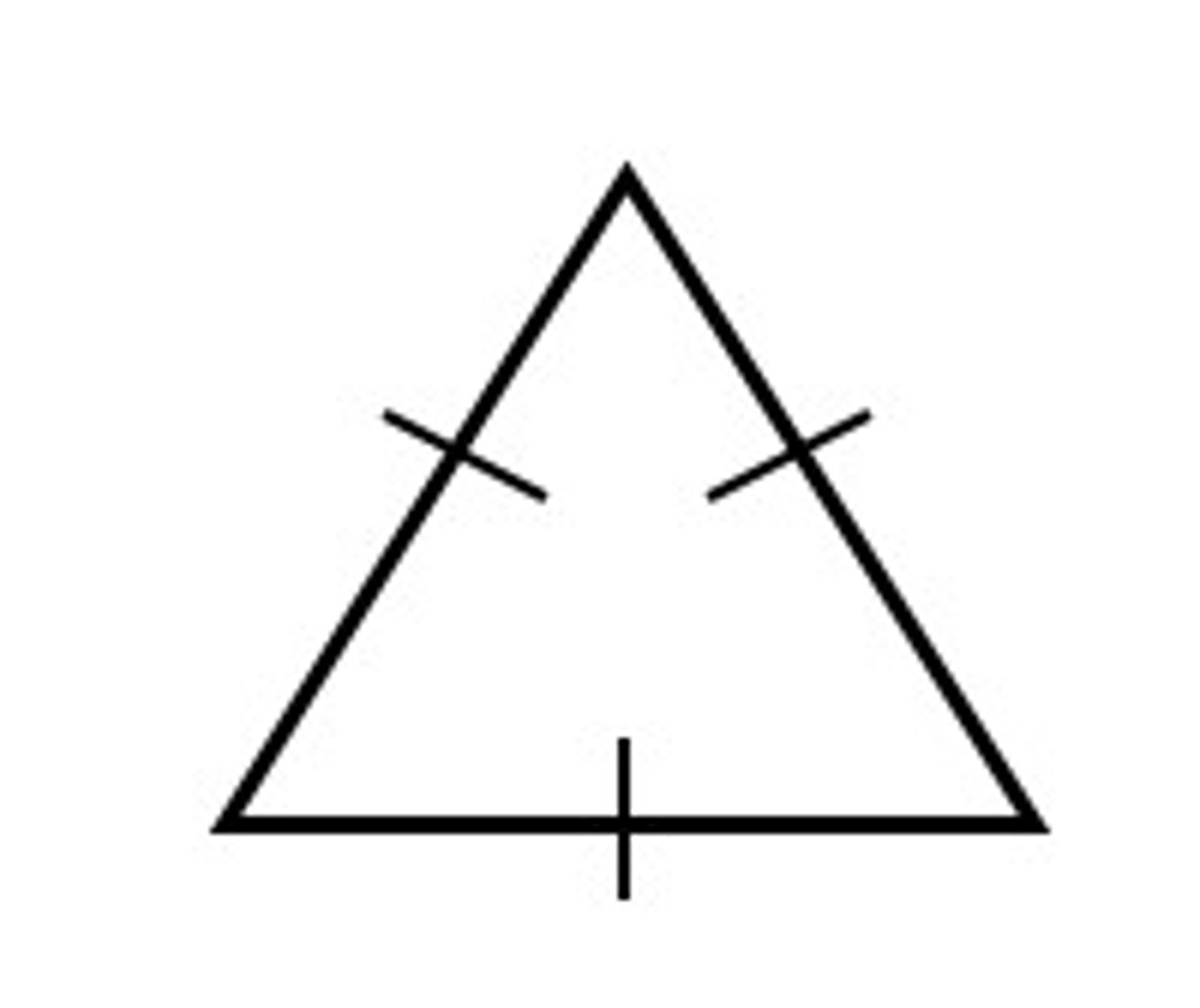
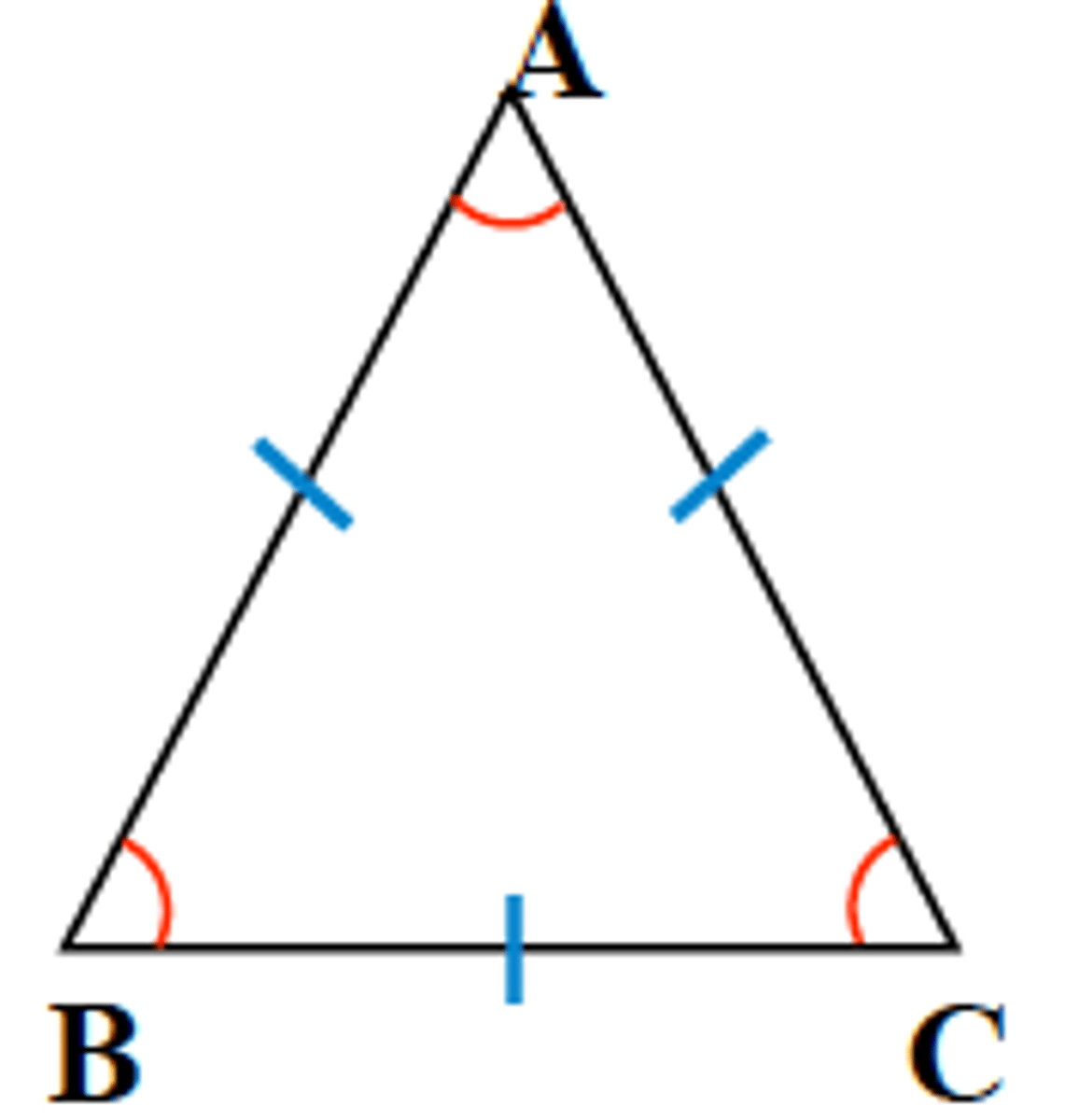
isosceles triangle theorem and its converse

if two sides of a triangle are congruent, then the angles opposite them are congruent. if two angles in a triangle are congruent, then the sides opposite them are congruent

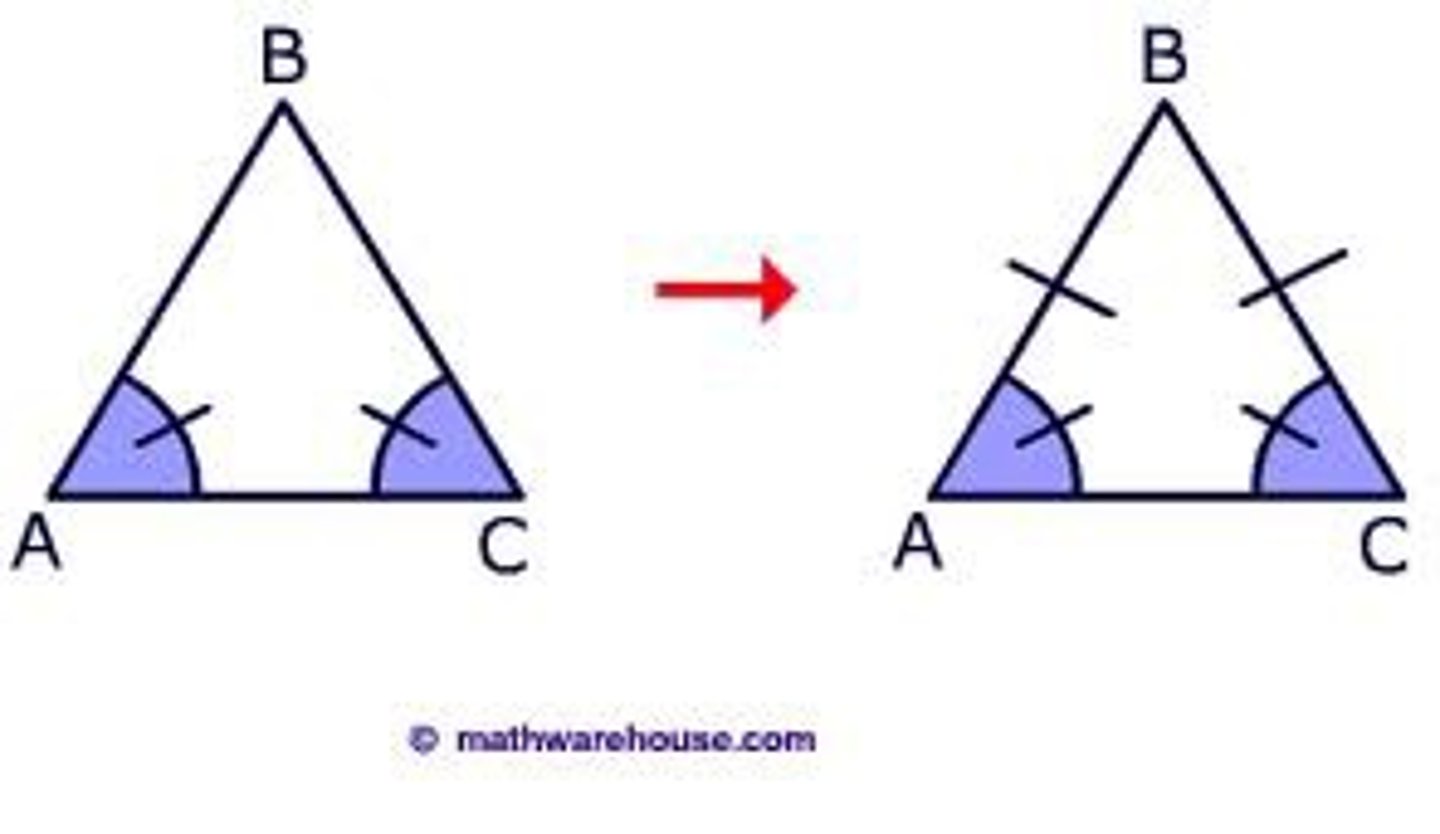
equilateral triangle theorem

all interior angles of an equilateral triangle measure 60º

Pythagorean theorem

In a right triangle, the sum of the squares of the legs equals the square of the hypotenuse

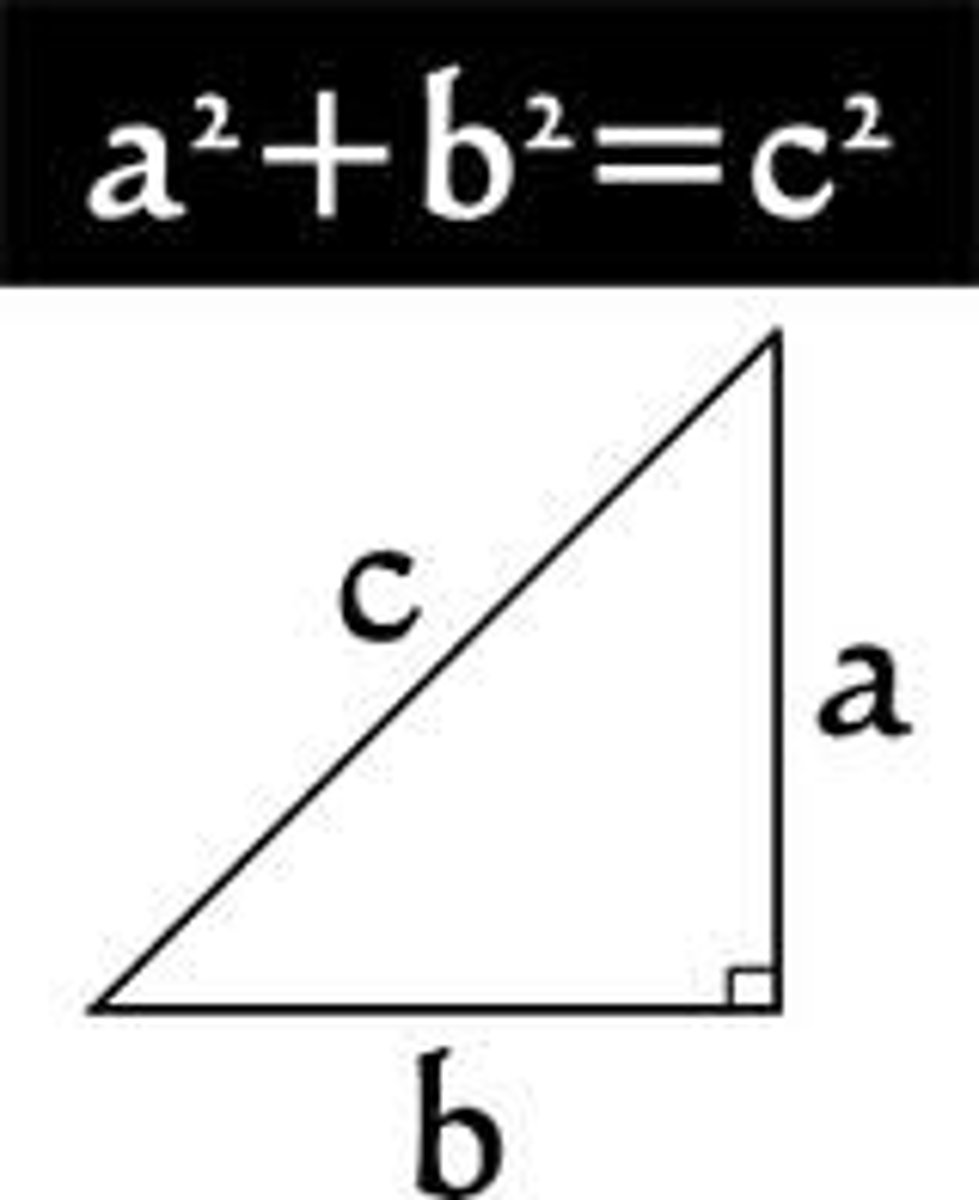
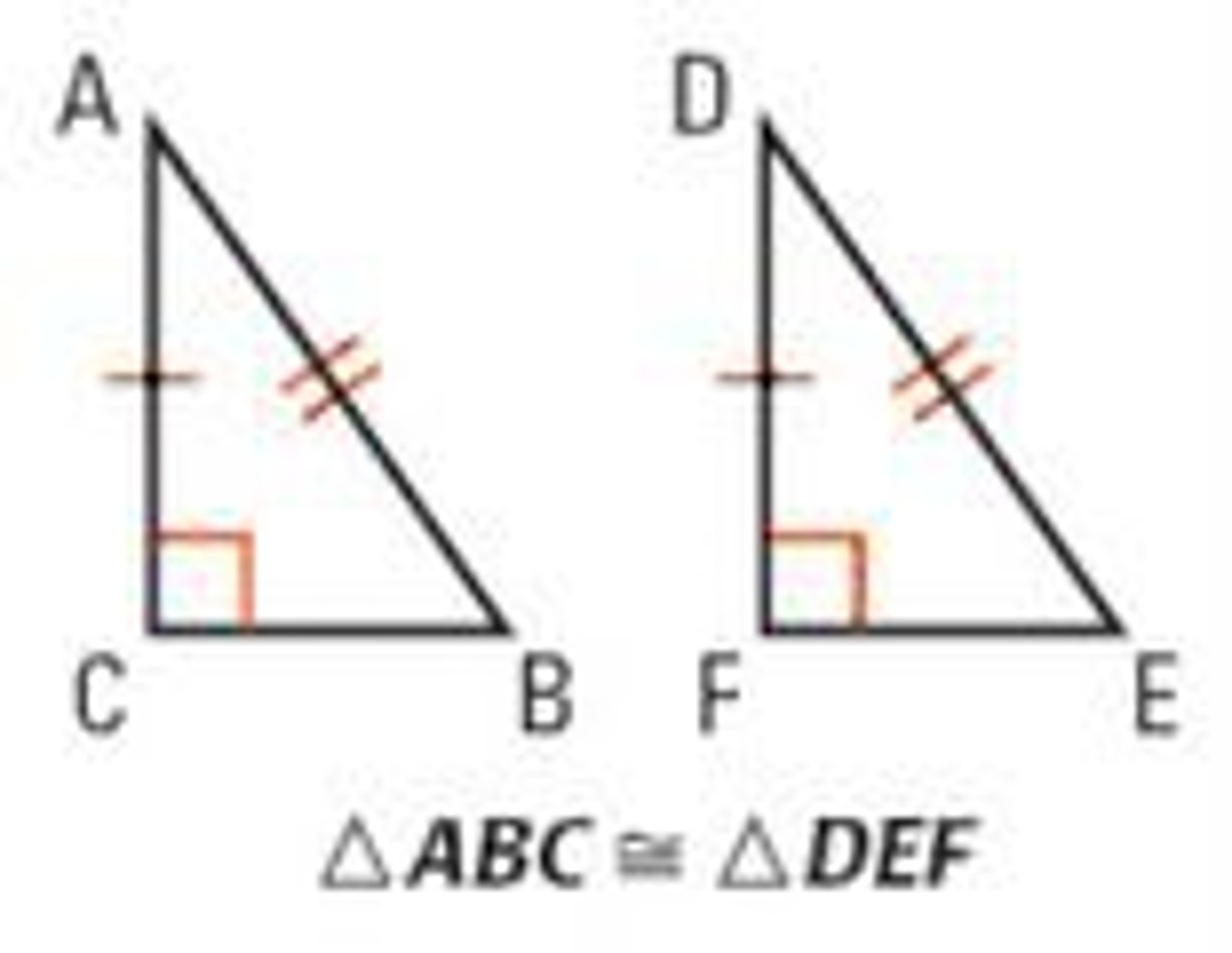
congruence

if two figures can be mapped onto another by a sequence of rigid motions.

reflexive property of equality

Any quality is equal to itself . For figures, any figure is congruent to itself

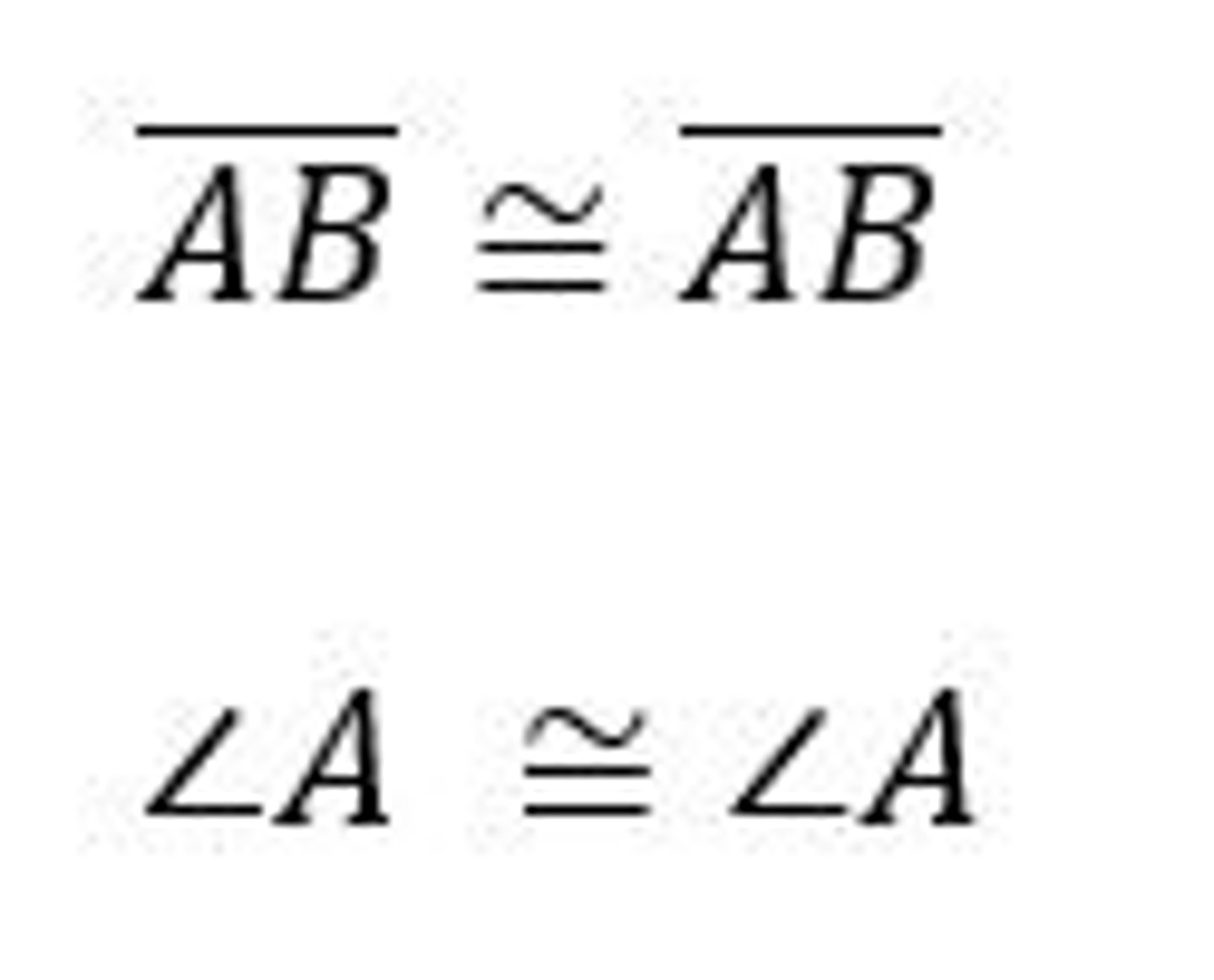
slope formula

Y₂-Y₁/X₂-X₁ (RISE/RUN)

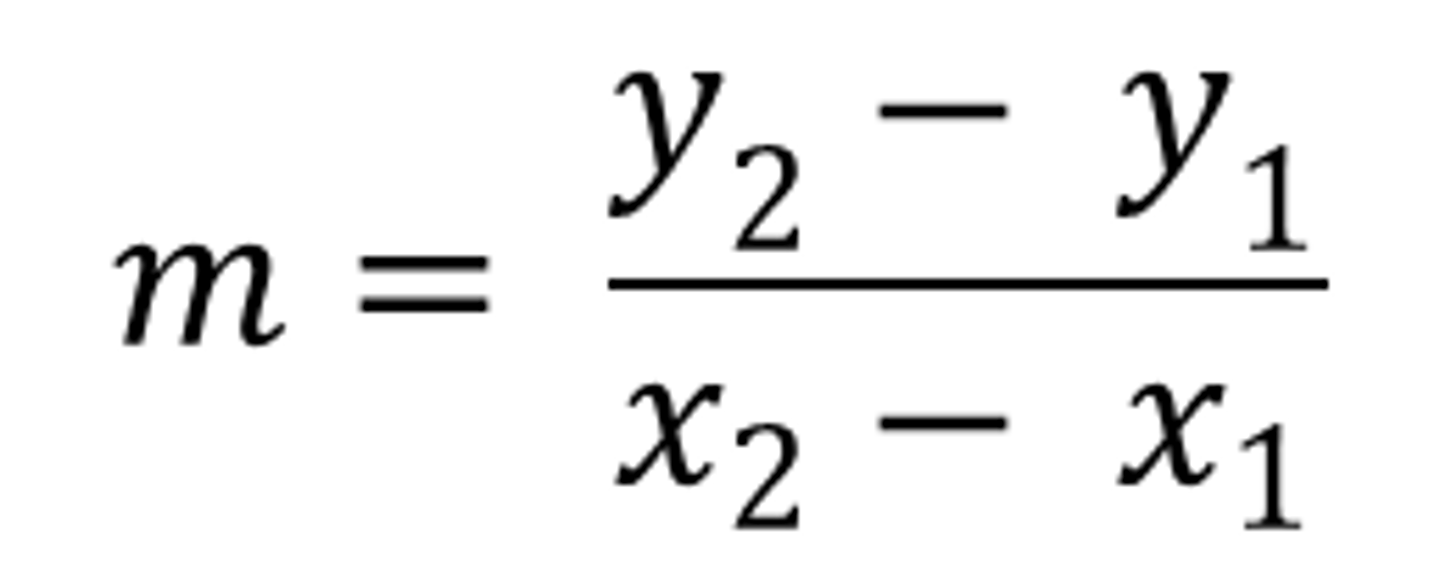
Distance formula

√(X₂-X₁)²+(Y₂-Y₁)²

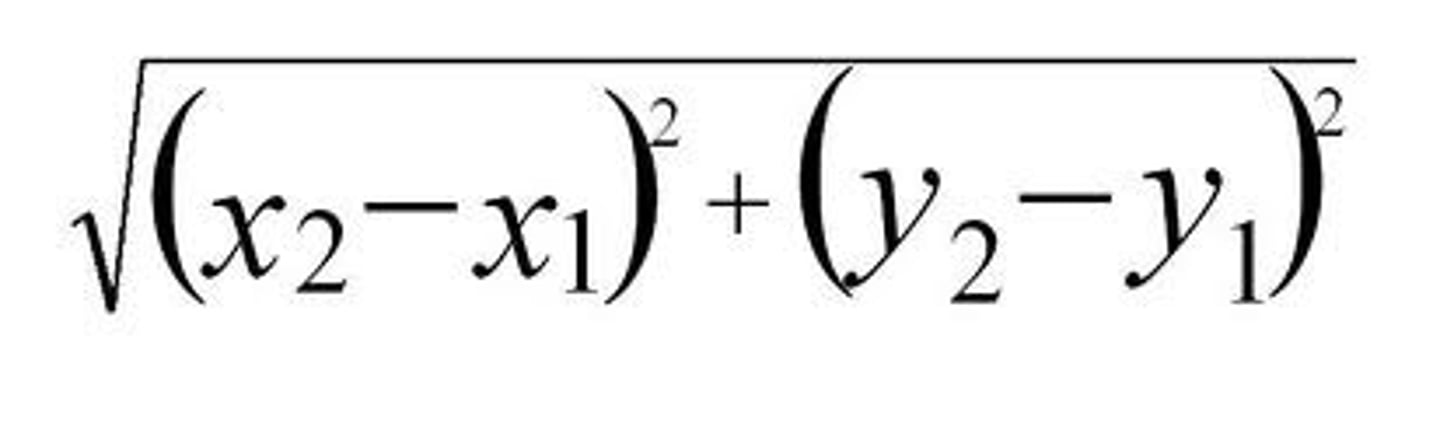
how to find the area of a polygon on a graph

sketch a rectangle around the shape. find the areas of the triangles between the polygon and the rectangle. find all the areas of the triangles, add them up, and subtract them from the area of the rectangle.

collinear

three points are collinear if the slopes between any two pairs are equal

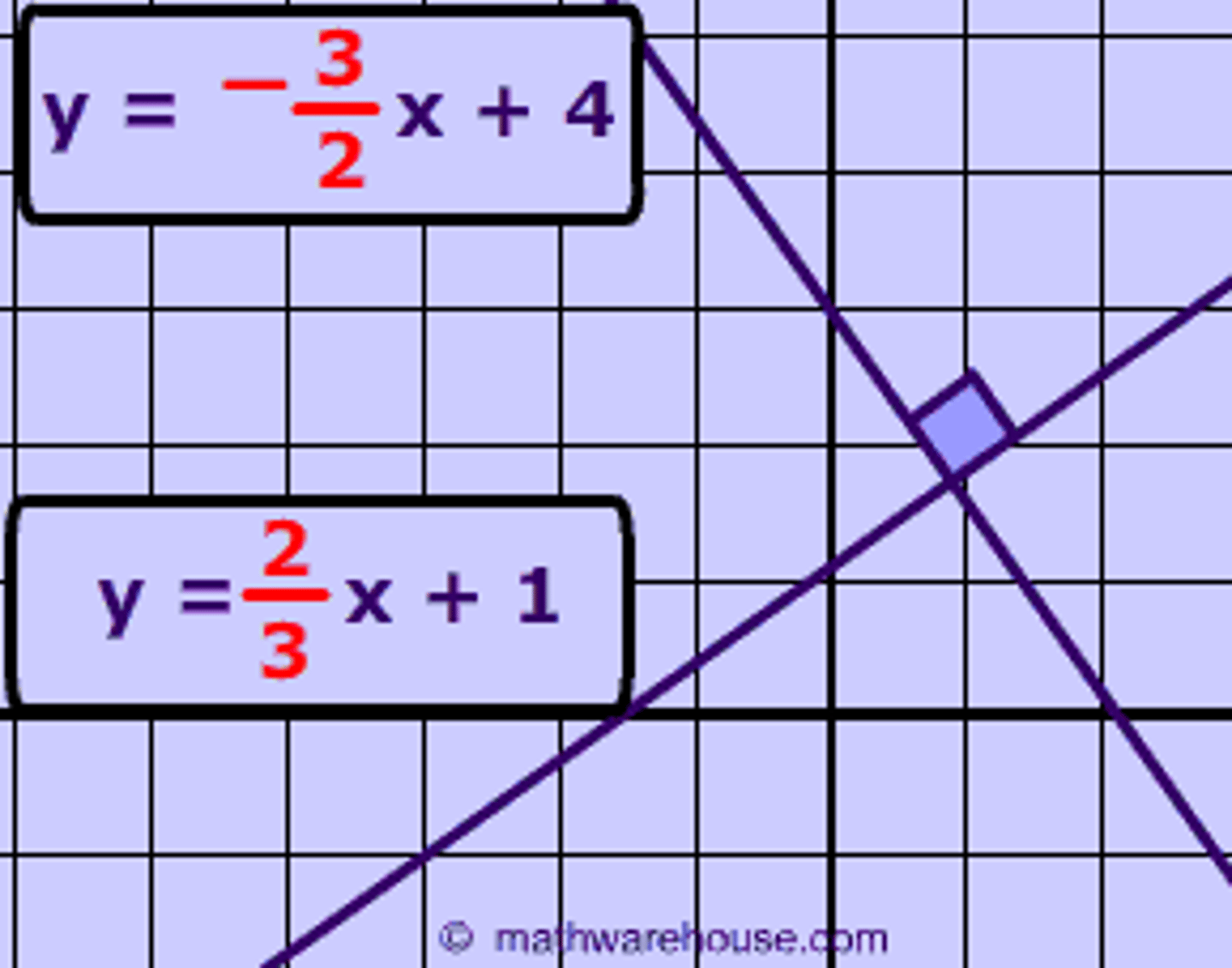
slope of a line= slope of perpendicular line

2/3=-3/2

segment parallel to a side theorem

-If a segment intersects two sides of a triangle such that a triangle similar to the original triangle is formed, the segment is parallel to the third side

Side splitter theorem

A segment parallel to a side in a triangle divides the two sides it intersects proportionally

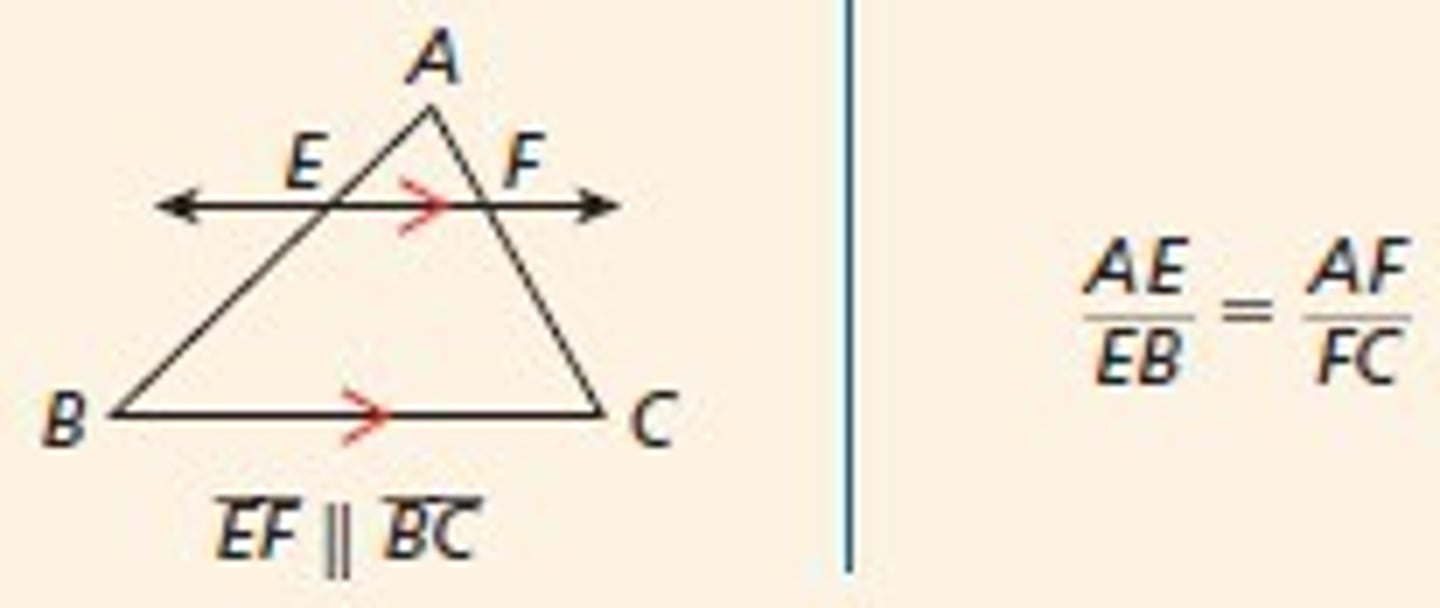
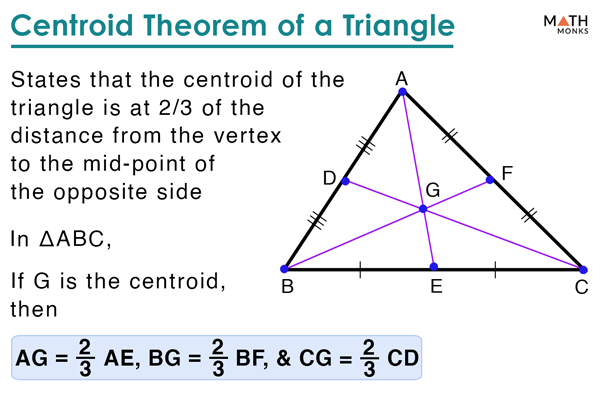
centroid theorem

the centroid of a triangle divides each median in a 1:2 ratio, with the longer segmant having a vertex as one of its endpoints

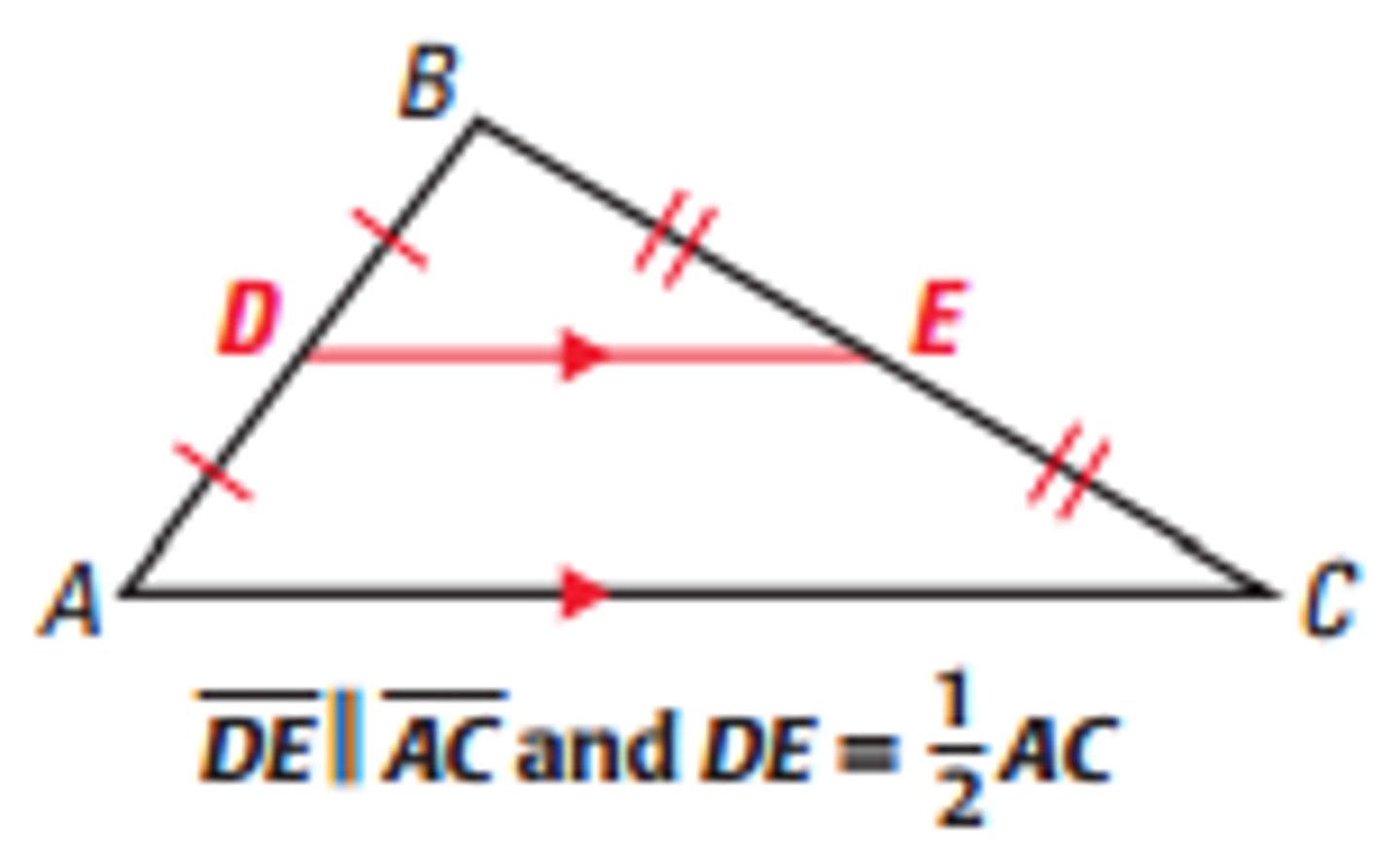
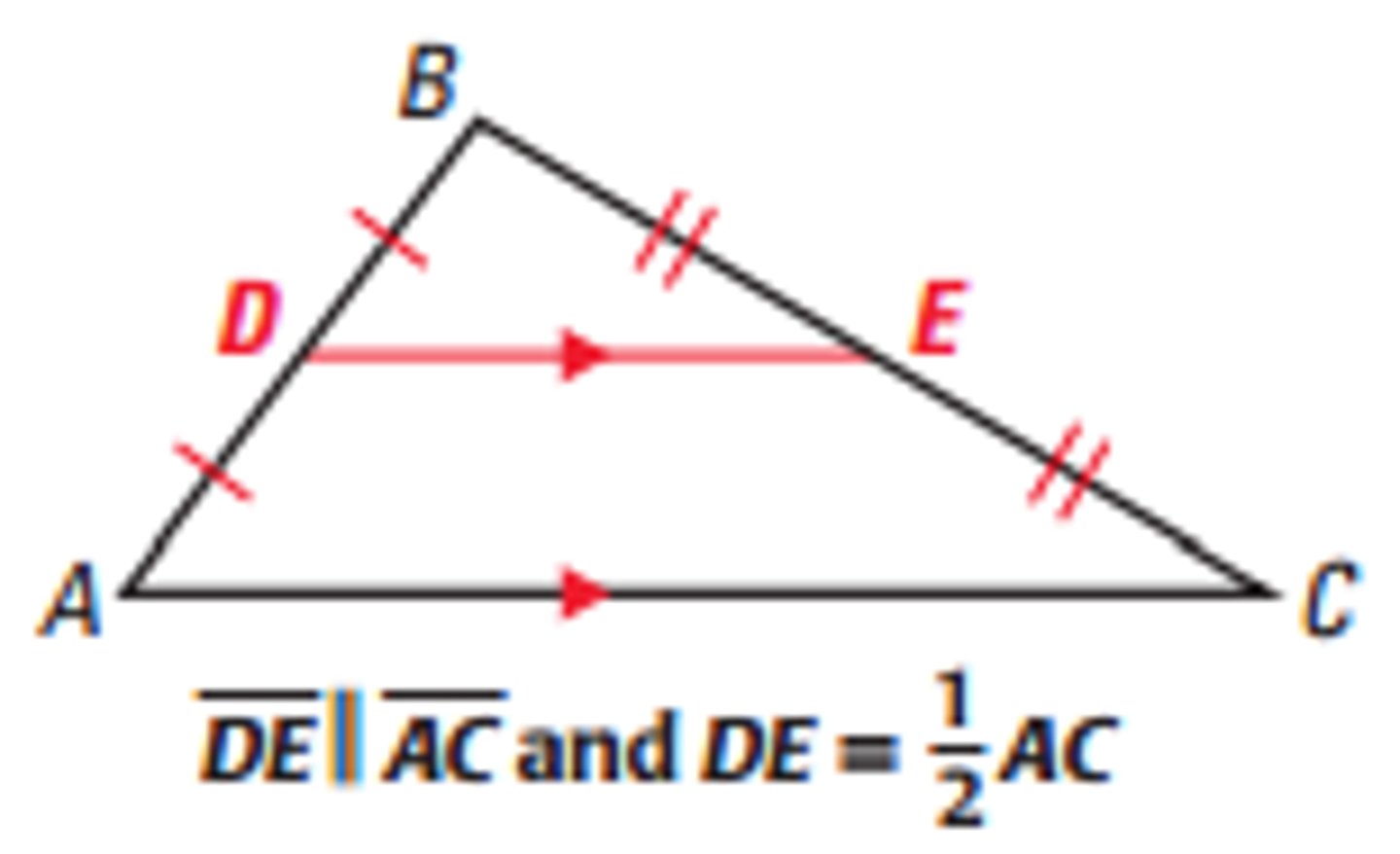
midsegment theorem

a segment joining the midpoints of two sides of a triangle (a midsegmant) is parallel to the opposite side, and it's length is equal to 1/2 the length of the opposite side

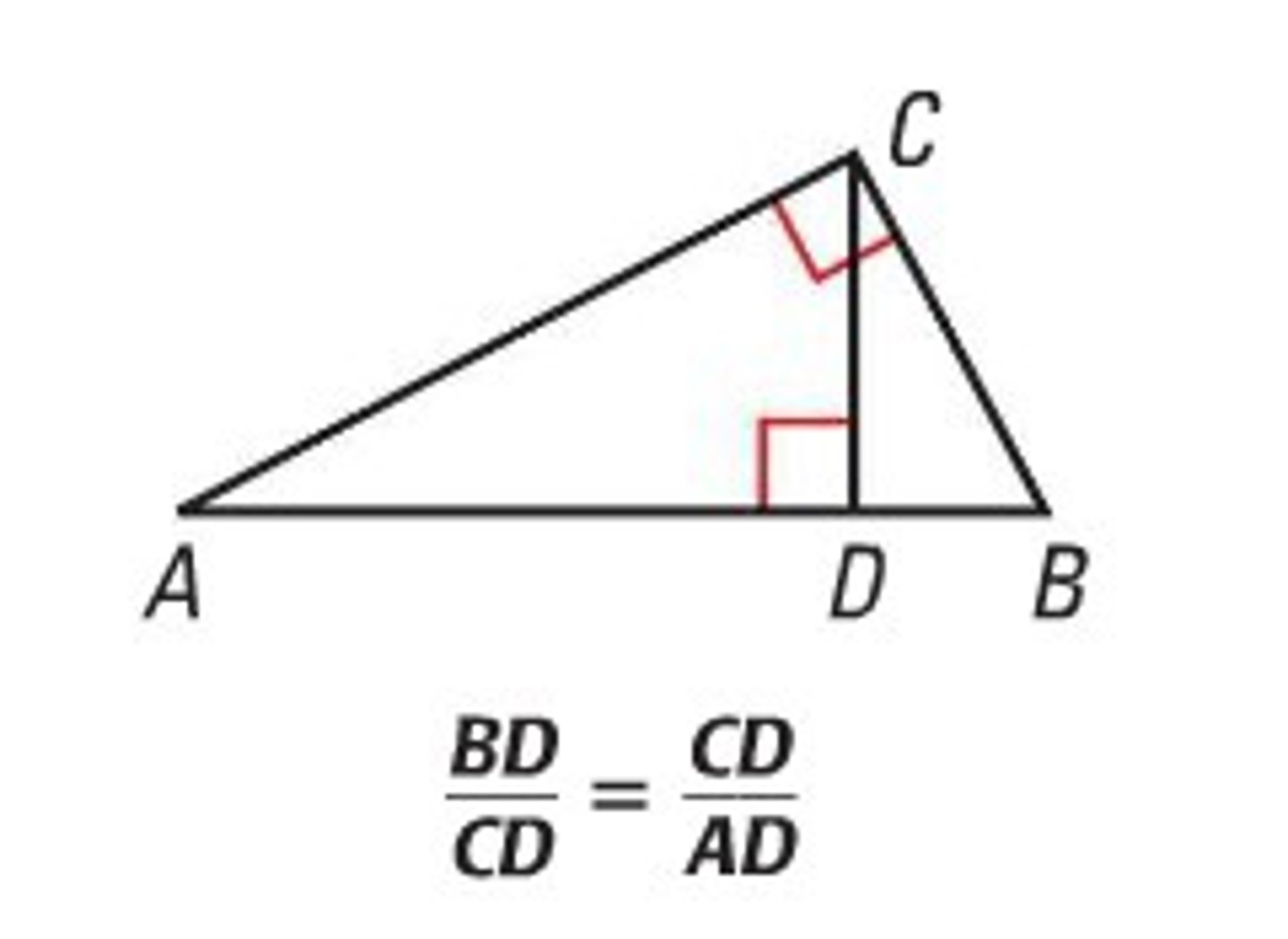
altitude to the hypotenuse of a right triangle theorem

the altitude to the hypotenuse of a right triangle forms two triangles that are similar to the original triangle

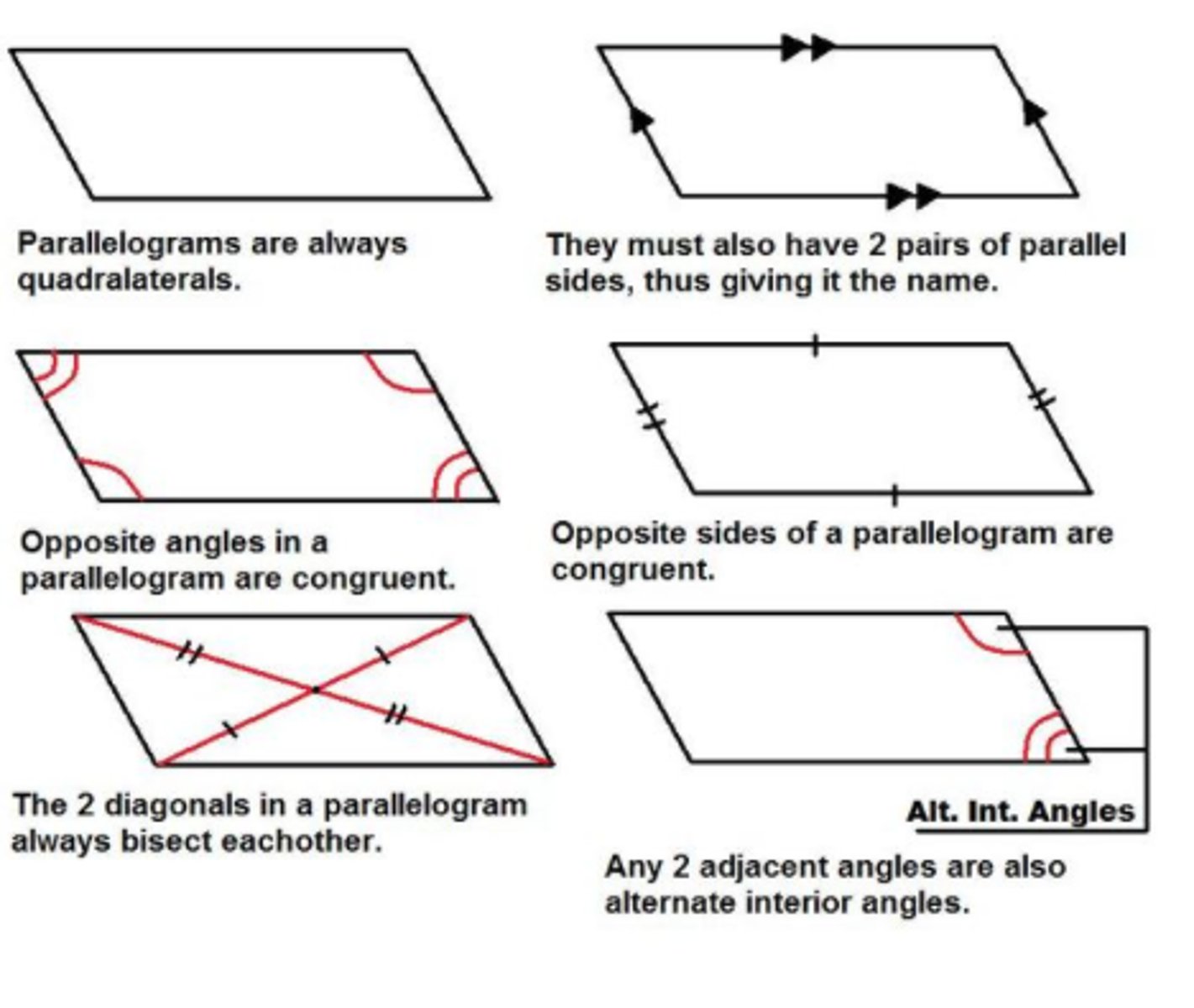
parallelogram properties

Opposite sides are parallel and =. Opposite angles are congruent. adjacent angles are supplementary. The diagonals bisect each other.diagonals divide the parallelogram into two = triangle

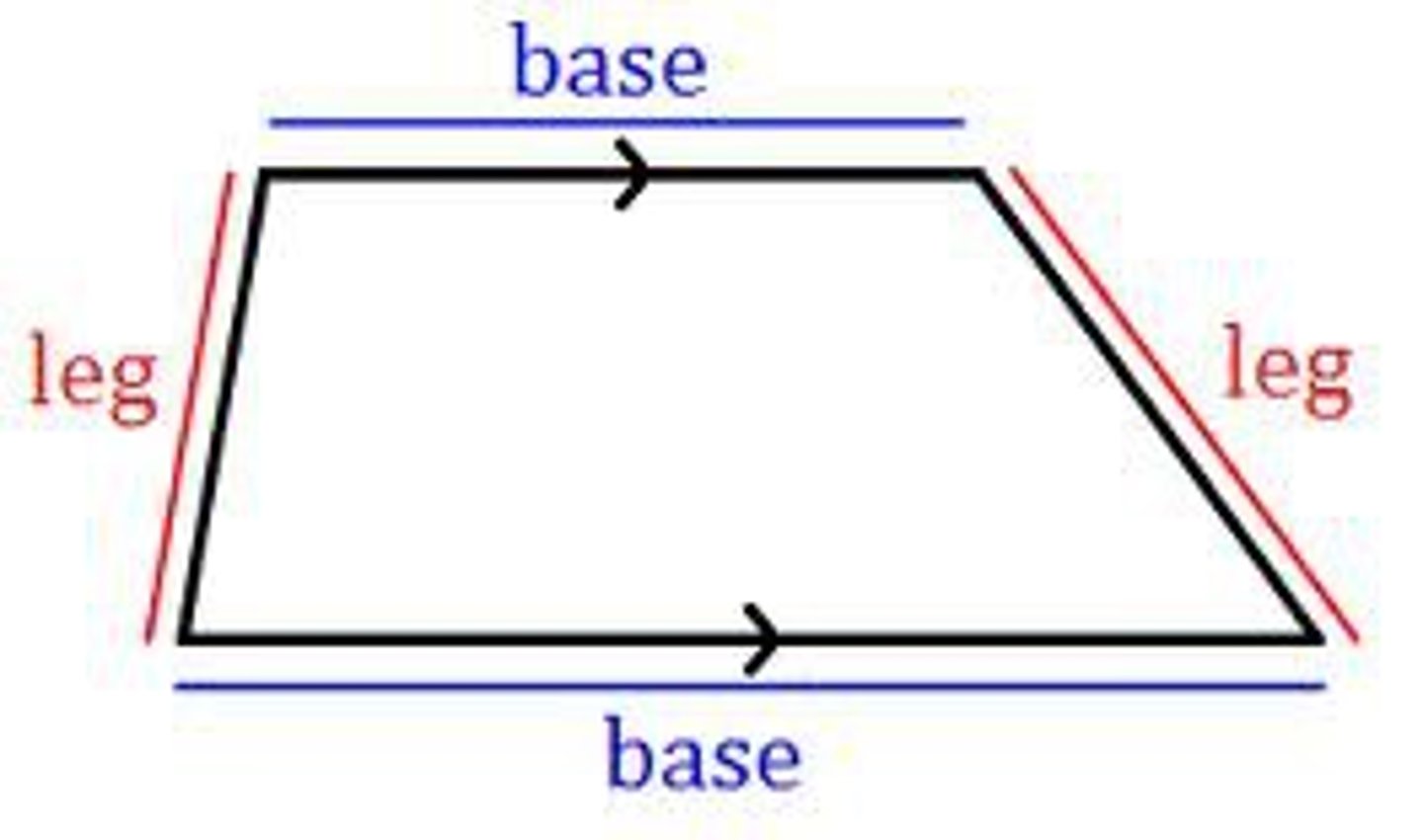
trapezoid properties

one pair of parallel sides. Each lower base angle is supplementary to the upper base angle on the same side.

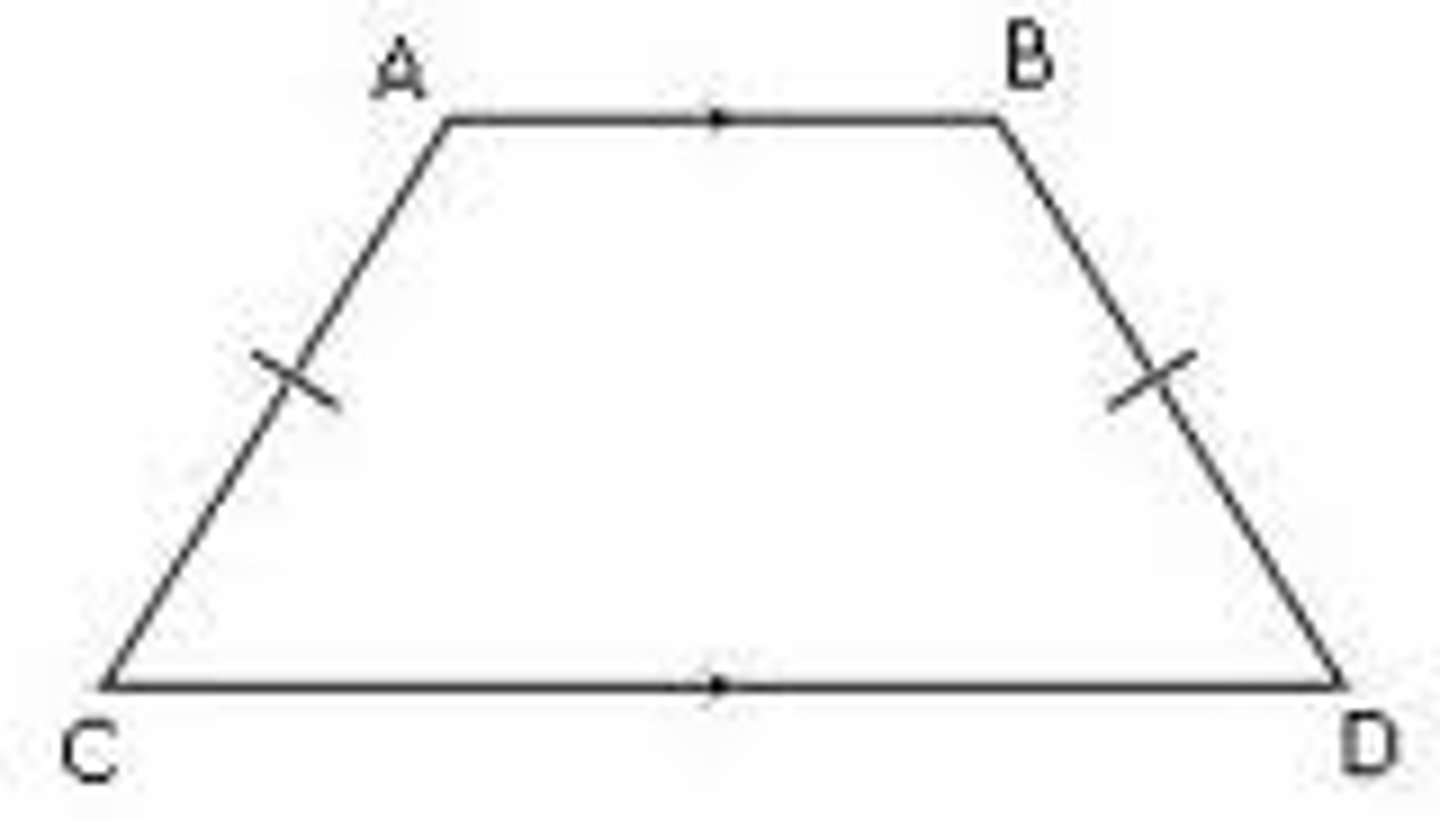
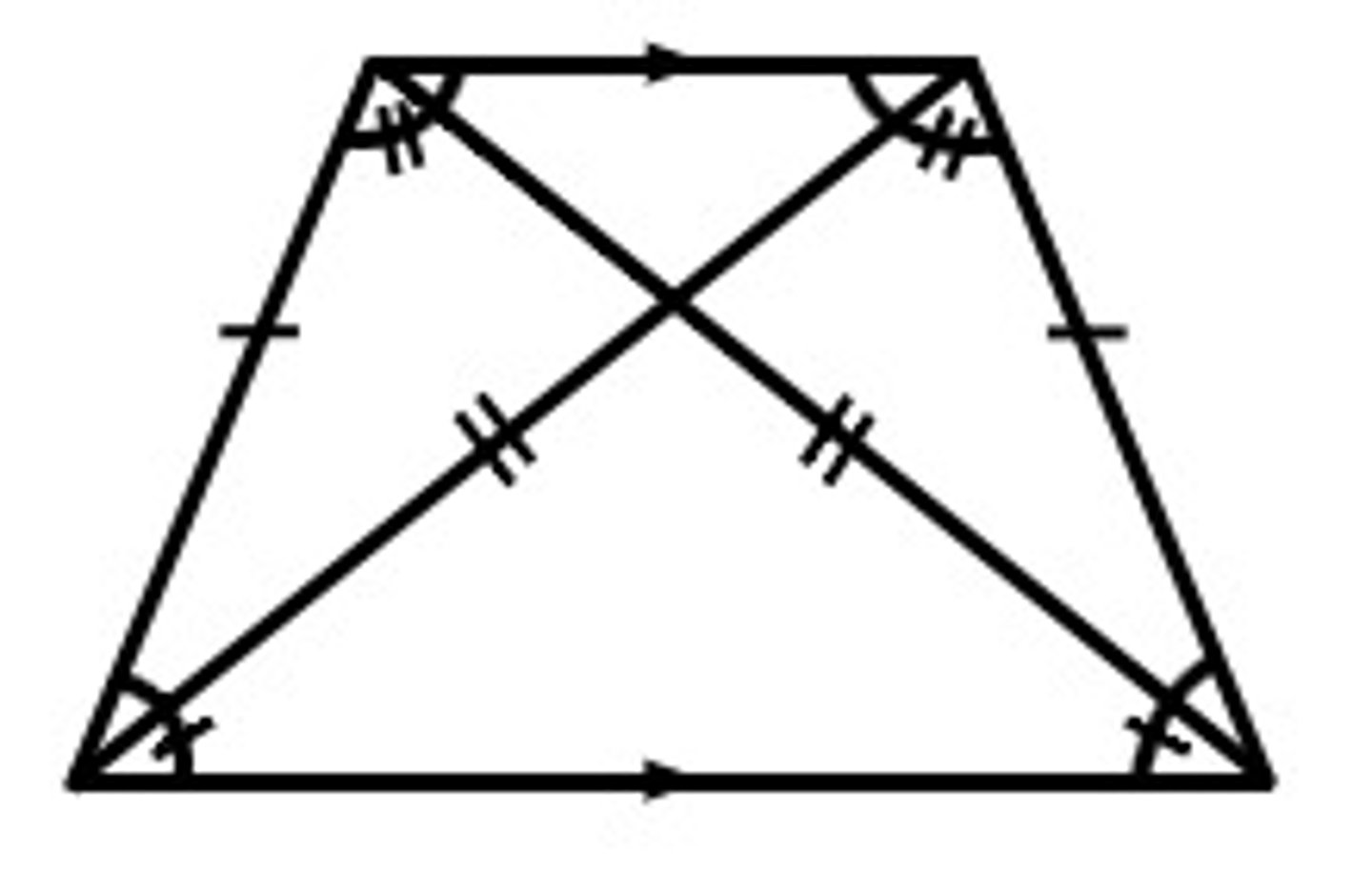
isosceles trapezoid properties

legs congruent, lower and upper base angles congruent, Any lower base angle is supplementary to any upper base angle, diagonals congruent

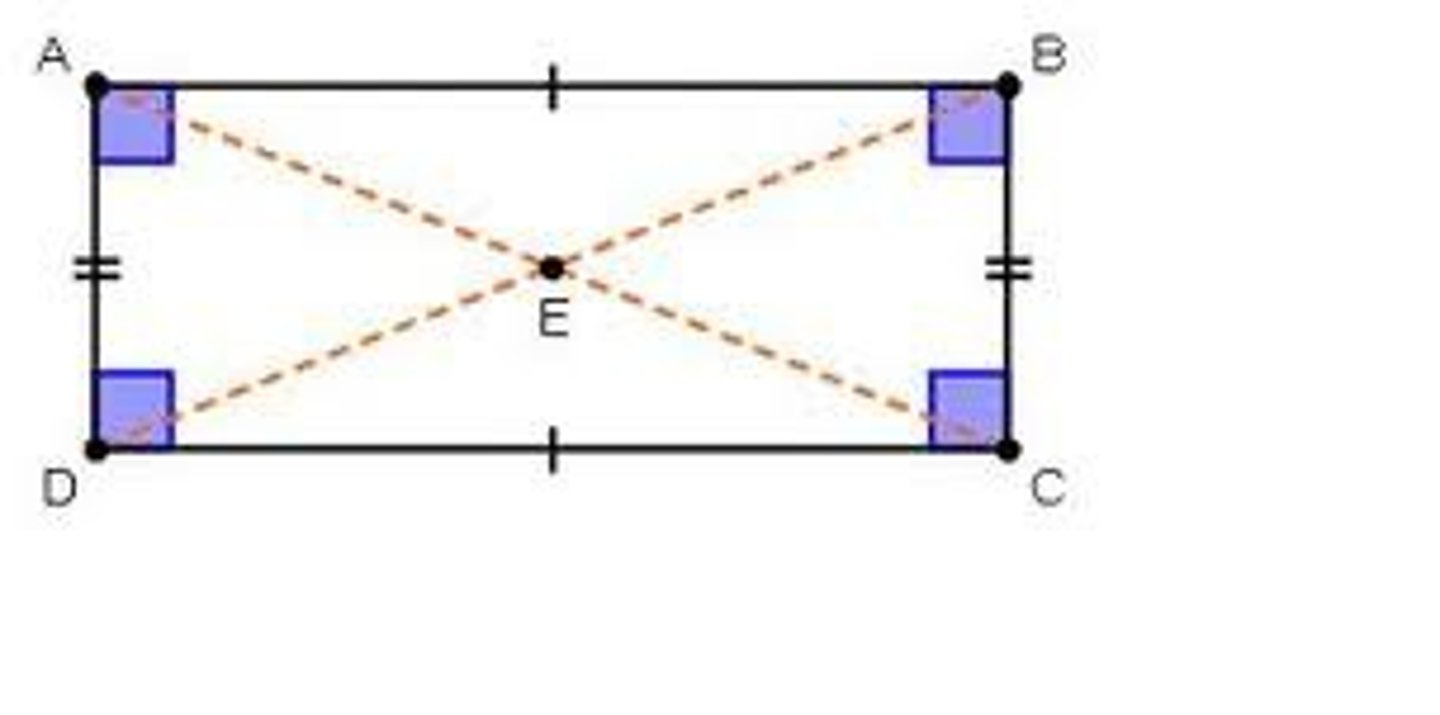
rectangle properties

parallelogram properties (opposite sides congruent). All right angles, diagonals are congruent

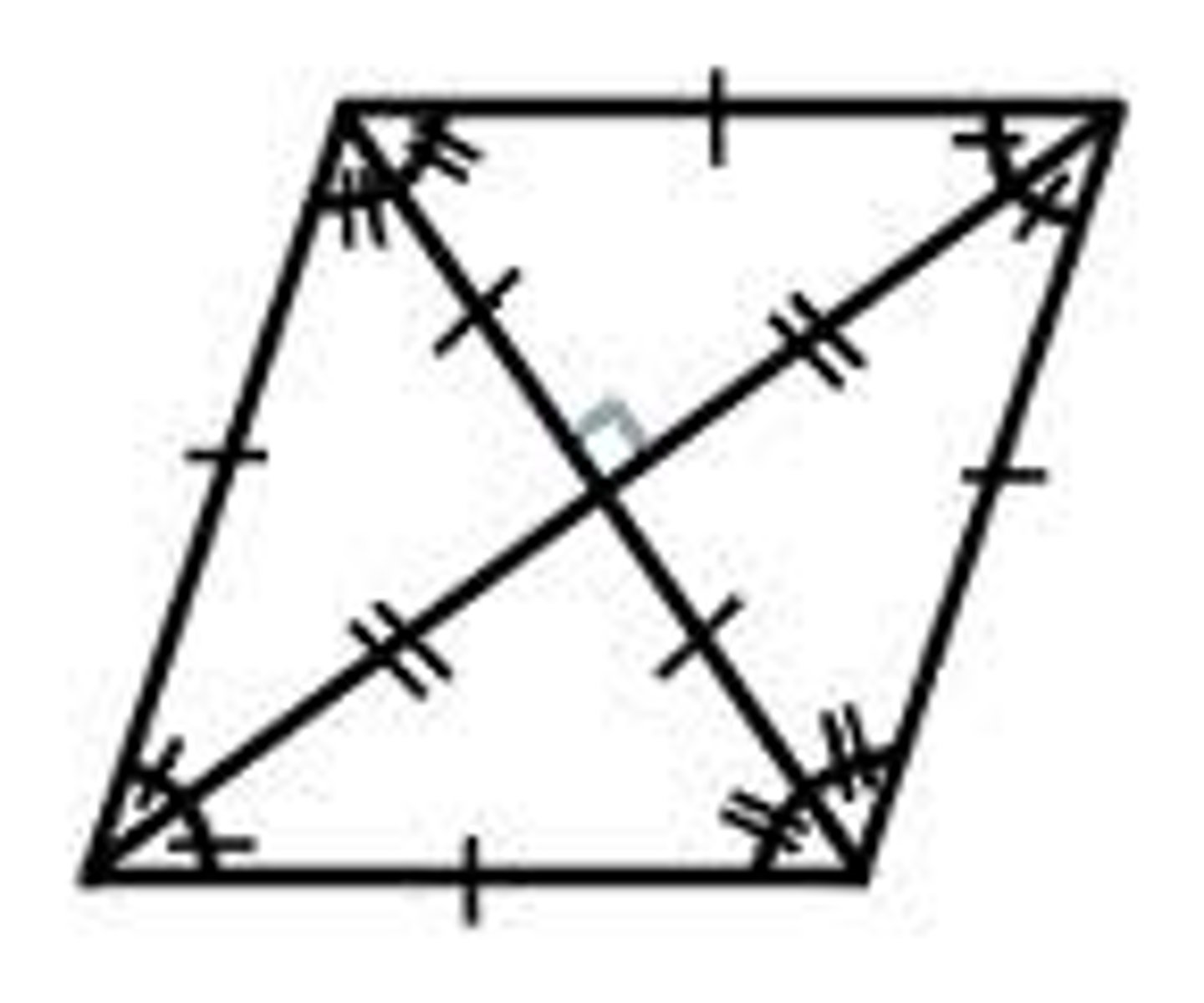
rhombus properties

parallel sides, opposite angles are congruent, consecutive angles are supplementary. all sides =. diagonals bisect angles.diagonals are perpindicular bisectors of each other DIAGNOLS FORM FOUR CONGRUENT ISOSCELES RIGHT TRIANGLES

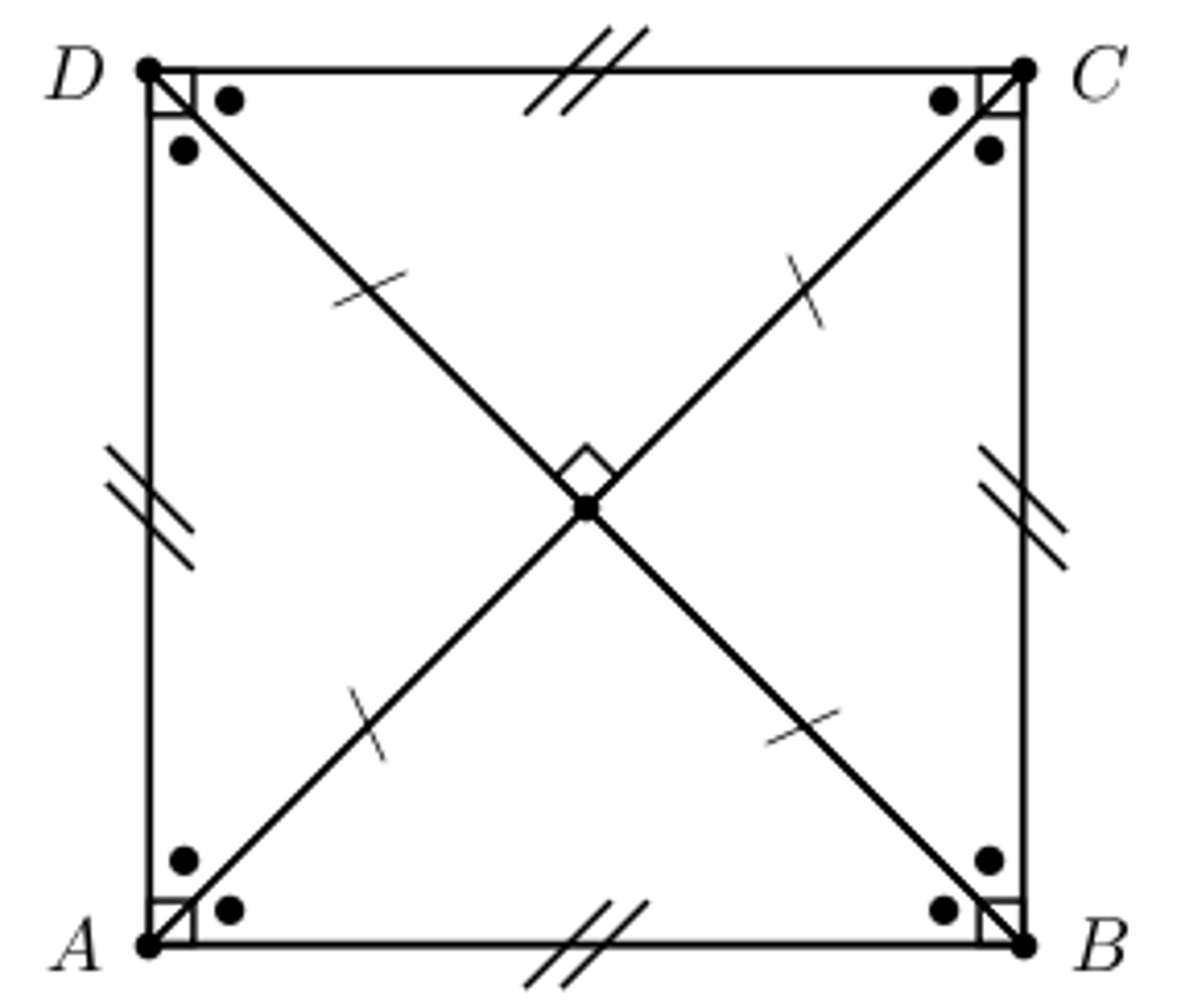
square properties

(for proofs) any one of the parallelogram + square + rhombus properties

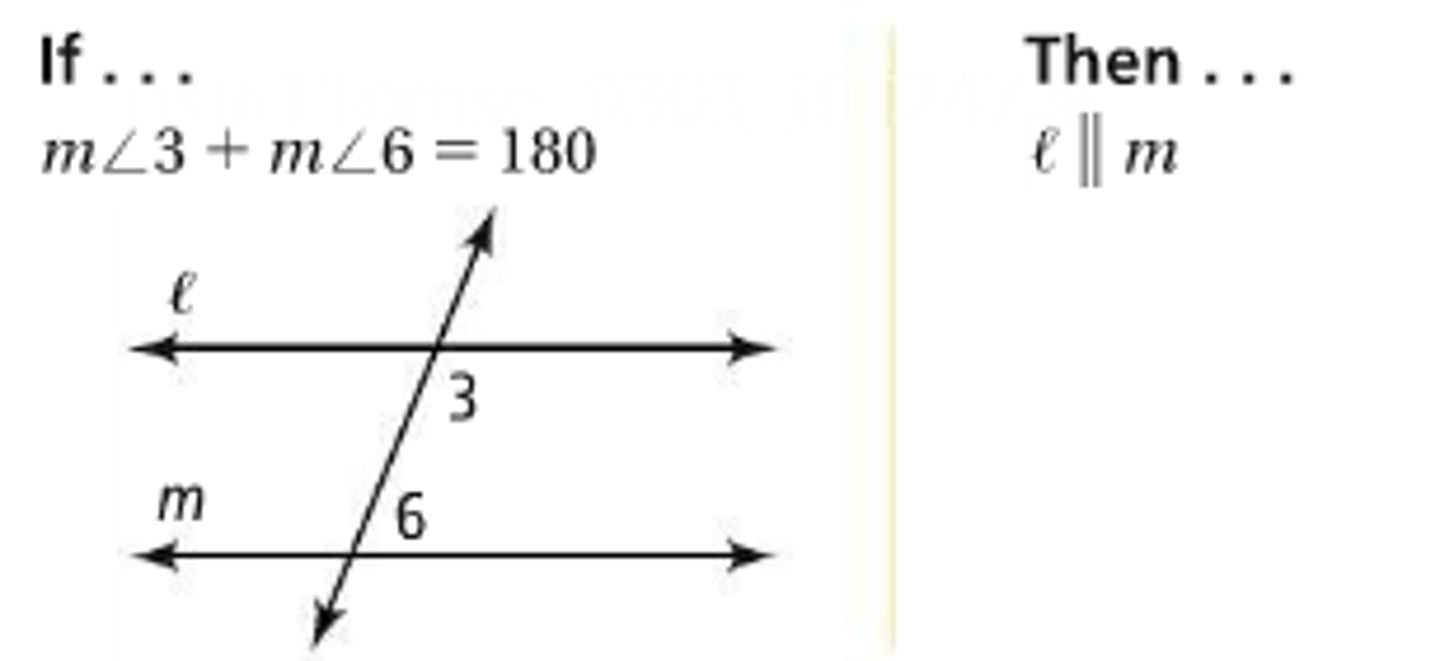
two lines are parallel

if the alternate interior angles formed are congruent

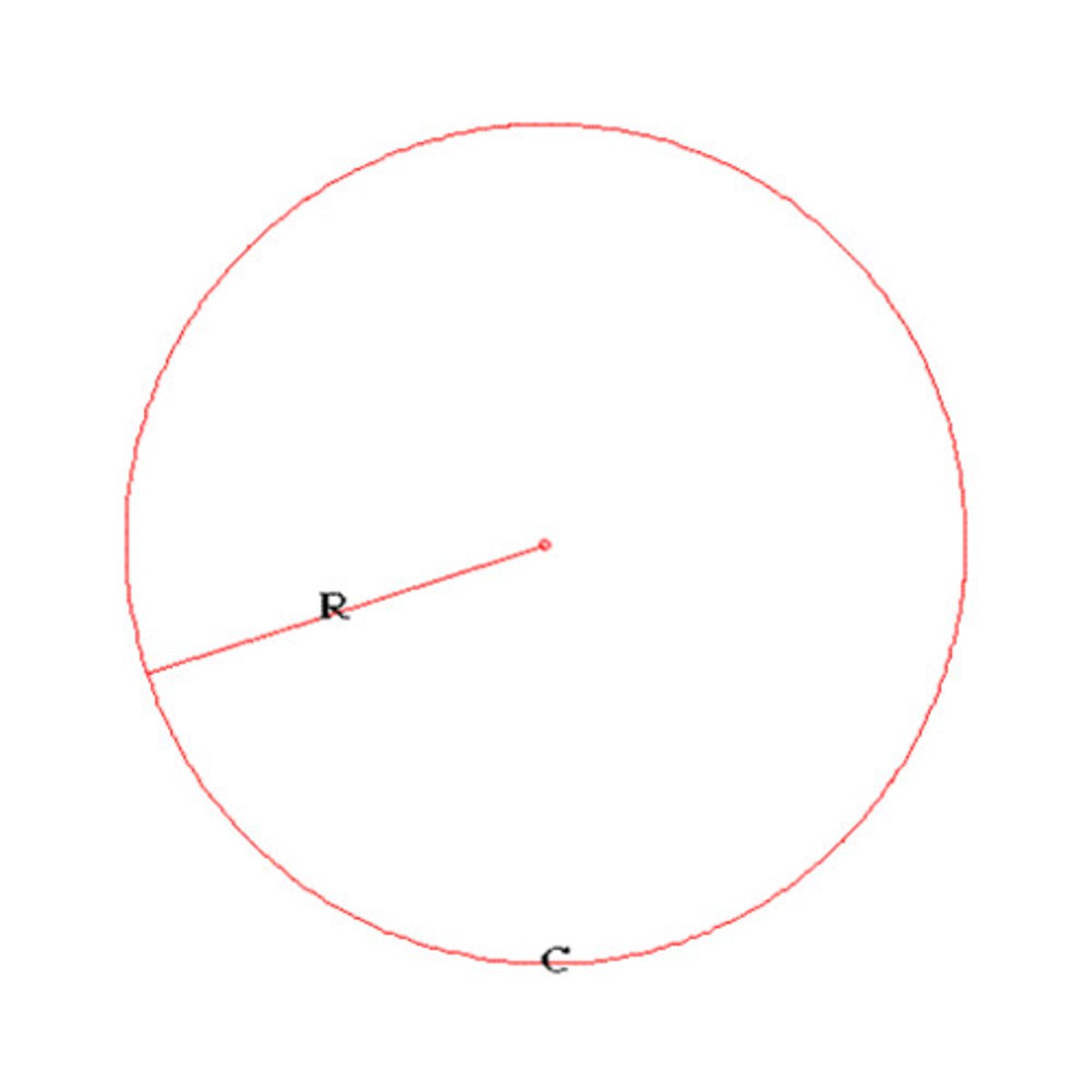
radius

a segment with one endpoint at the center of the circle and one endpoint on the circle

chord

a segment with both endpoints on the circle

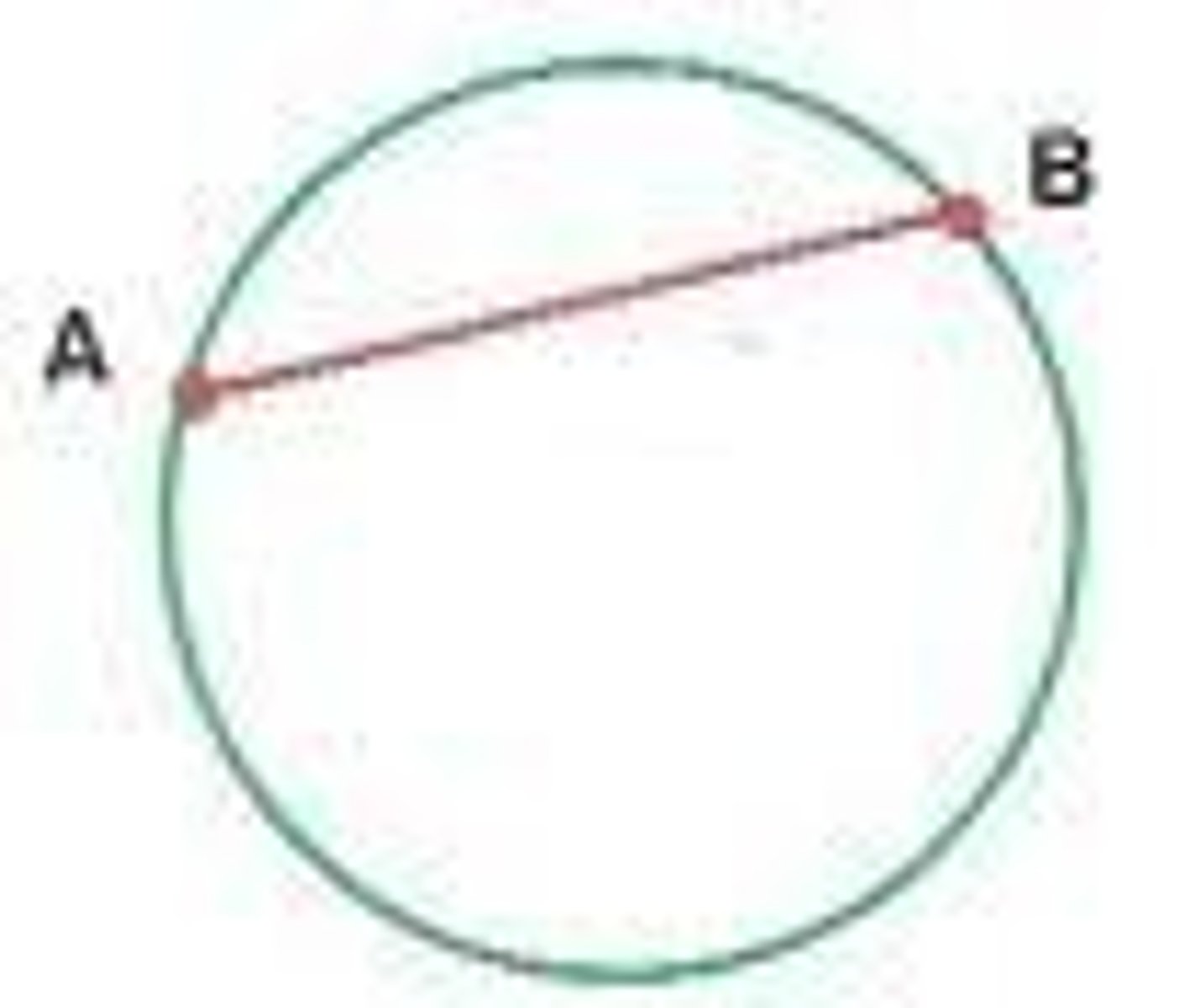
diameter

a chord that passes through the center of the circle

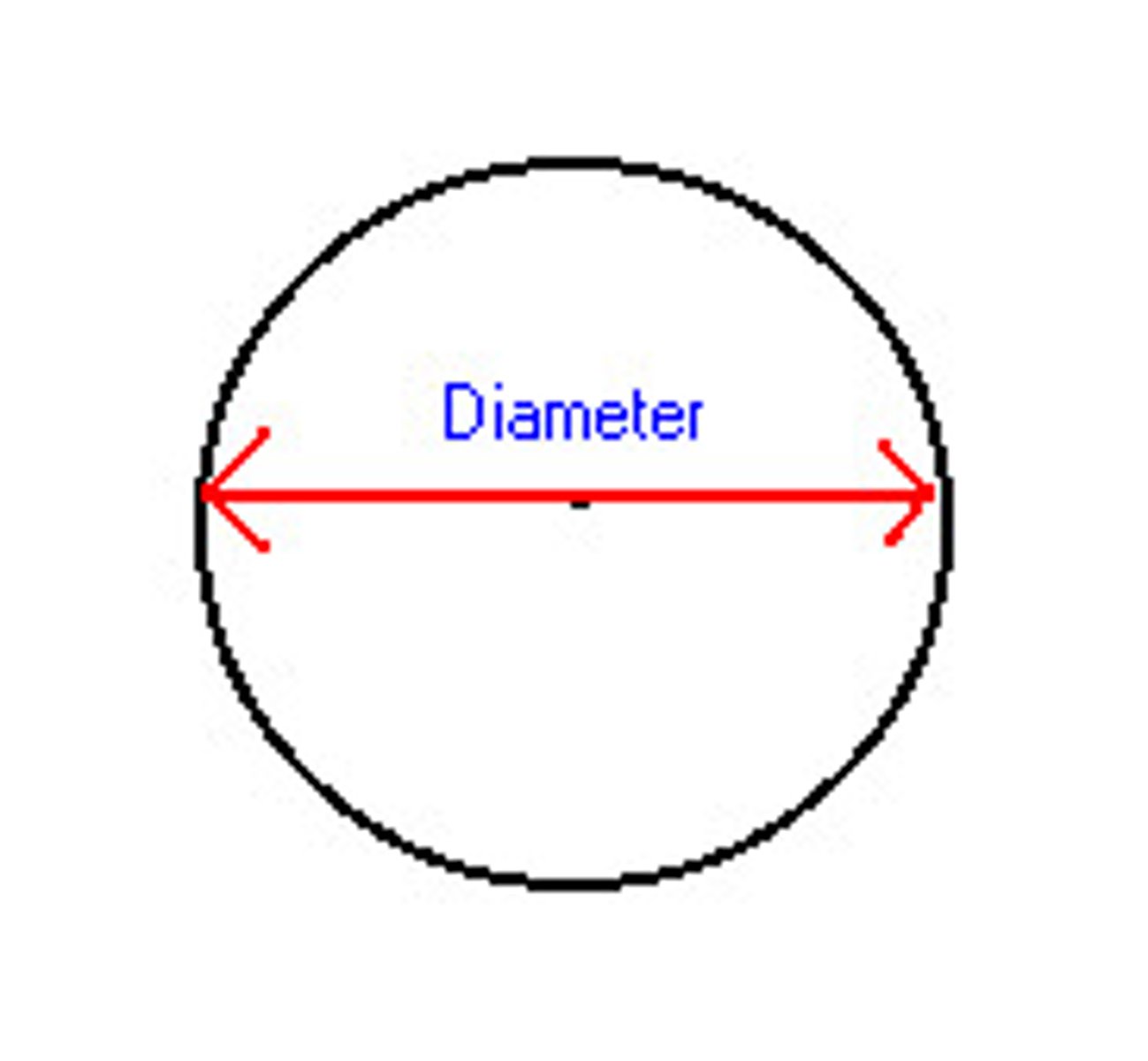
secant

a line that intersects a circle at exactly two points

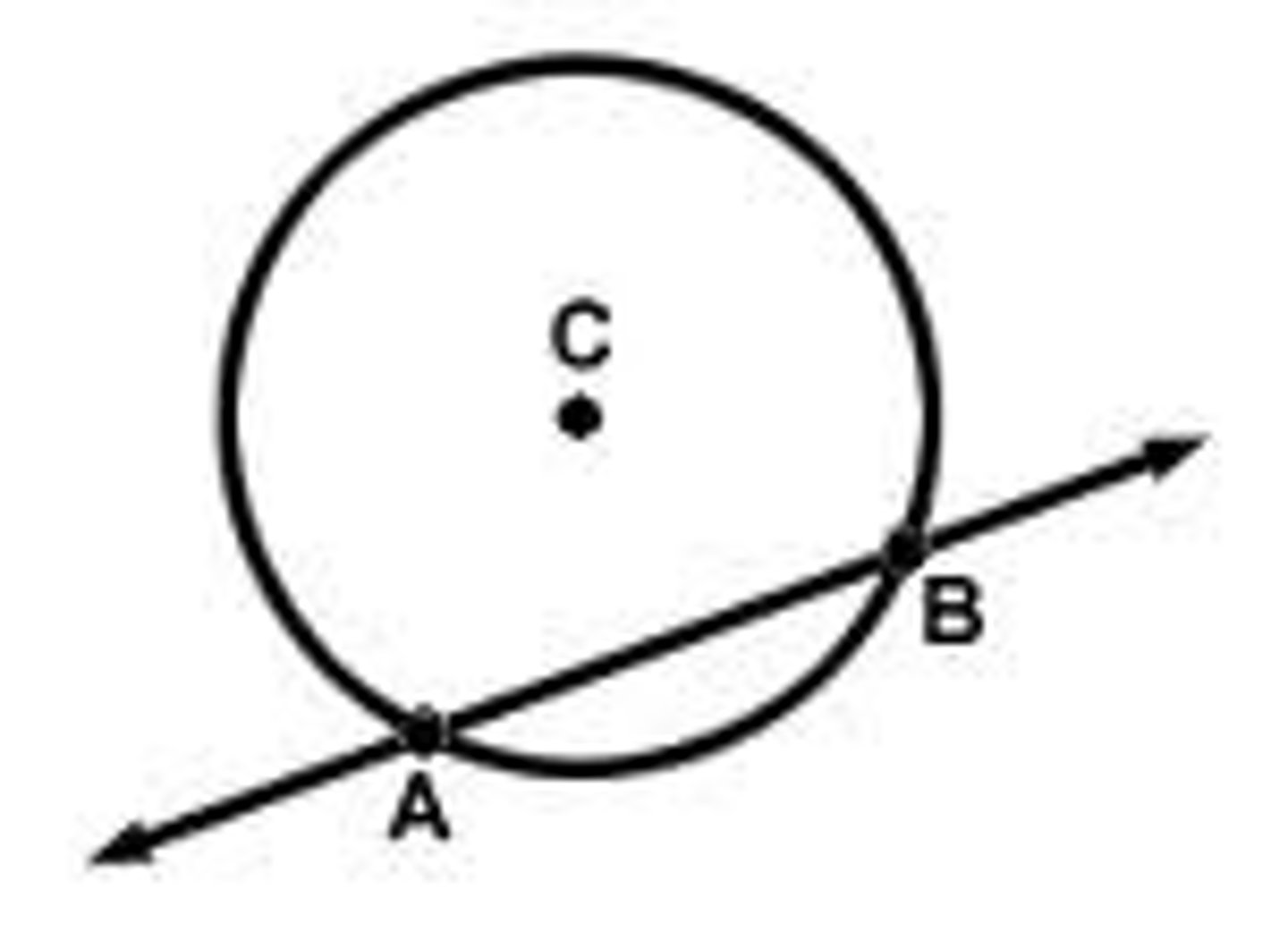
tangent

a line that intersects a circle at exactly at one point

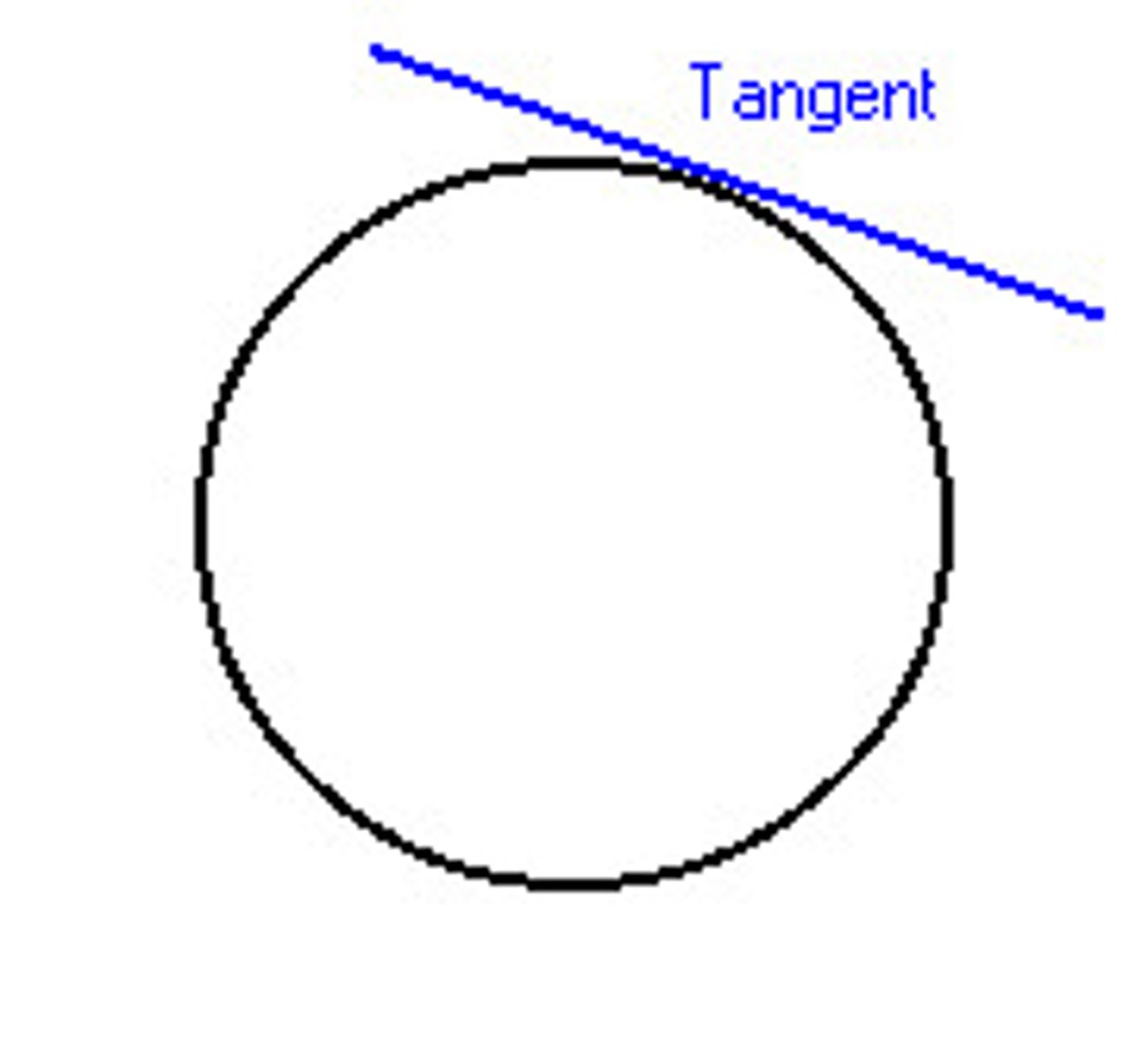
point of tangency

the point at which a tangent intersects a circle

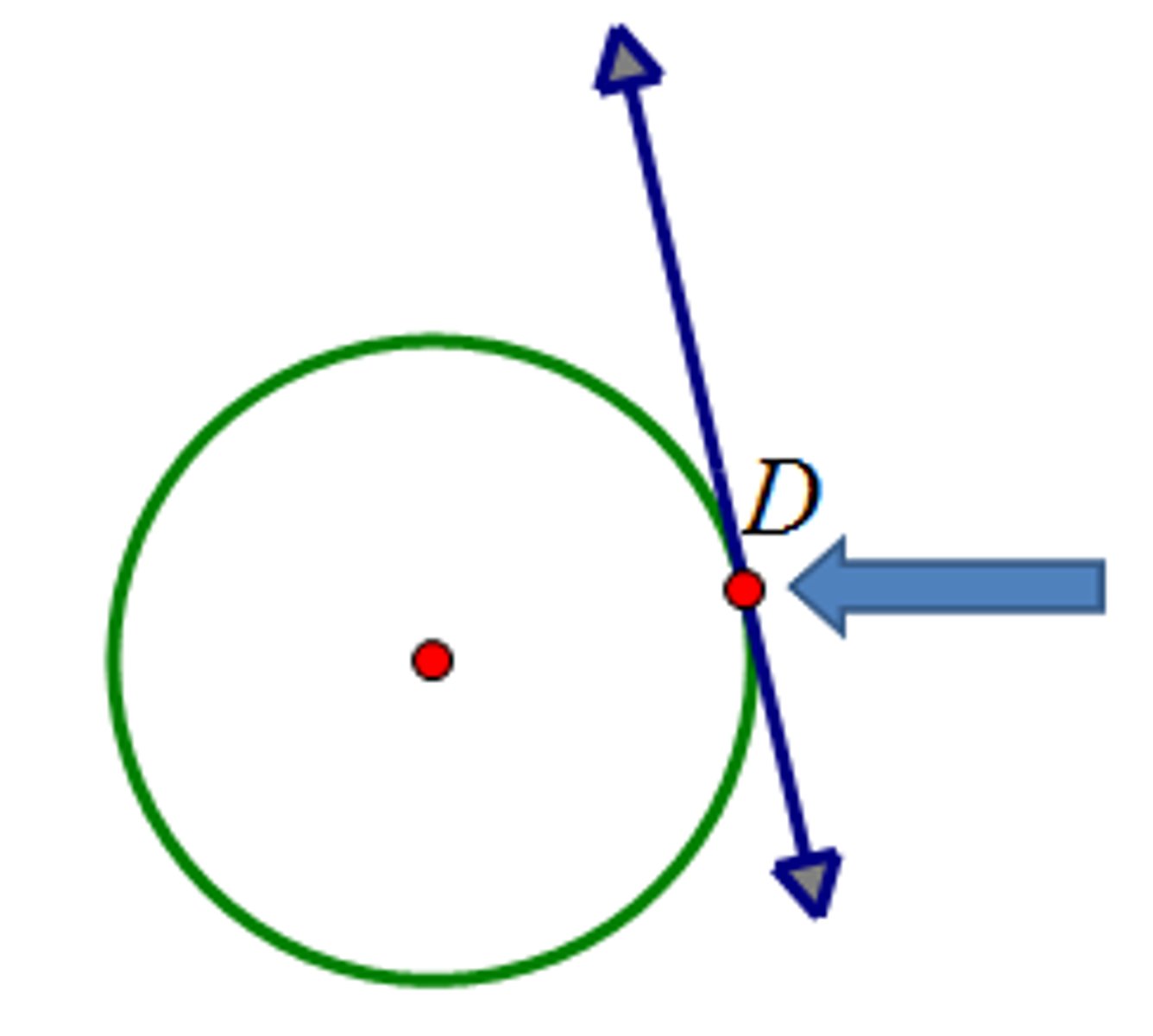
radii properties

all radii of a given circle are congruent, two circles are congruent if and only if their radii are congruent