Quantum Mechanics term 2

Current flow through a surface in 1 dimension

\frac{\partial j}{\partial x}=-\frac{\partial\rho}{\partial t}

Swapping coordinates of two identical particles

• symmetric if bosons

• antisymmetric if fermions

Free electron (loosely bound valence electrons) model of a metal

• non-interacting fermions

• moving in potential from uniform +ve charged background

• system neutral

Fermi wavenumber

k_{F}=\frac{N\pi}{2L}

the radius of the Fermi Sphere

Fermi Energy

E_{F}={{\displaystyle}}\frac{{{\displaystyle\hbar}}}{2m}\left(\frac{3\pi^2N}{V}\right)^{\frac23}

Highest energy state occupied by fermions at absolute zero

Density of states

n\left(E\right)=\frac{L}{\pi}\left(\frac{2m_{e}}{{{{{\displaystyle\hbar}}}}^2}\right)^{\frac12}\frac{1}{\sqrt{E}}

Where do allowed states sit?

on a grid in wavevector space

Fermi velocity

group velocity of wavepacket with wavevector grouped around the fermi wavevector

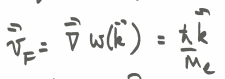
Fermi-dirac distribution

f\left(E,\mu,T\right)=\frac{1}{\exp\left(\frac{E-\mu}{k_{B}T}\right)-1}

Heat capacity

C_{V}=\frac{dE_{tot}}{dT}

Magnetic susceptibility

\chi=\frac{dM}{dB}=\mu_{B}^2n\left(E_{F}\right)

spherical approximation of nuclei

scattering experiments show nucleus can be modelled as sphere with radius R₀A^1/3

Neutrons and protons key facts

• fermions

• magnetic moments

• interact with magnetic fields

Nuclear binding energy

energy required to break a nucleus into its constituent protons and neutrons

Characteristics of the strong nuclear force

• independent of charge

• short range (~fm)

• Nuclear matter constant density and constant binding energy per nucleon (roughly)

Liquid drop model of nuclei

treats nucleus as a droplet of incompressible nuclear material

Term 1 of binding energy of a nucleus from LDM

C_1A

• nuclear interactions show saturation

• C₁ extracted from data

Term 2 of binding energy of a nucleus from LDM

• nucleons on surface are less tightly bound than those in interior

• negative term

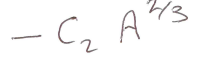
Term 3 of binding energy of a nucleus from LDM

-\frac{C_3Z\left(Z-1\right)}{A^{\frac13}}

• Each proton repels the other

• negative term

Term 4 of binding energy of a nucleus from LDM

-\frac{C_4\left(N-Z\right)^2}{A}

• nuclei need balance between energies of neutrons and protons

• N ~ Z for small nuclei

• N just larger than Z for larger nuclei

• negative term

Term 5 of binding energy of a nucleus from LDM

C_5A^{-\frac43}

• nuclear forces favour pairing of p and n

• positive term if Z and N are even

• negative if both are odd

• zero otherwise

Pauli exclusion principle

fermions cannot occupy the same state in space unless they have different spin states

Guidelines for electronic configurations

• fill up Z H-like energy states, labelled n, l, m_l and ↑↓

• for each n, there are n subshells labelled by increasing l from l = 0 (s,p,d,f)

• each subshell labelled by l takes up to 2 x (2l +1) electrons

Which subshells are close in energy?

• 3d, 4s

• 4d, 5s

• 5d, 6s

Which subshell is filled first? 4f or 6s

6s

Molecule modelling

• neglect kinetic energy of nuclei and solve electronic problem

• nuclei take positions that minimise electronic and nuclear coulomb energy

Density Functional Theory

• takes many electron problem and external influence from static nuclei

• focusses on dealing with electron charge density

perfect crystal lattice

generated by taking all points in a lattice with the same basis

Position vector describing a lattice

\underline{R}=n_1\underline{a}+n_2\underline{b}+n_3\underline{c}

• a b c non-coplanar vectors - the primitive vectors

• n₁, n₂, n₃ range over all integer values (+ve and -ve)

Volume of the parallelopiped that describes a unit cell of a 3D lattice

V_{c}=\underline{a}\cdot\left(\underline{b}\times\underline{c}\right)

• packing unit cells together fills all space

Bravais lattices

• 14 3d crystal structures with different symmetries

7 groups of Bravais lattices

• cubic

• tetragonal

• orthorhombic

• hexagonal

• trigonal

• monoclinic

• triclinic

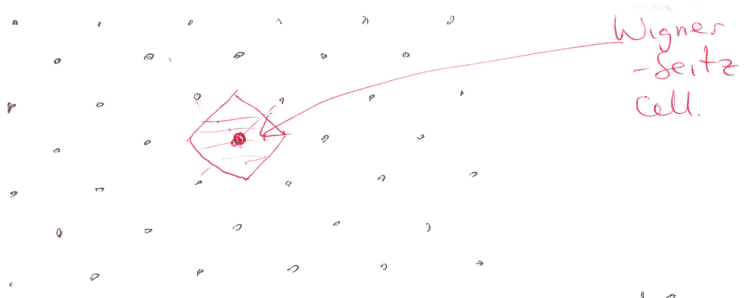
Wigner-Seitz cell

• the space enclosed by the planes that bisect and are perpendicular to vectors connecting a point to its nearest neighbours

• constructed around a single point

Reciprocal lattice use

Determining structure of crystals using X-ray diffraction that probe the reciprocal lattice

Position vector for a reciprocal lattice and its coefficients

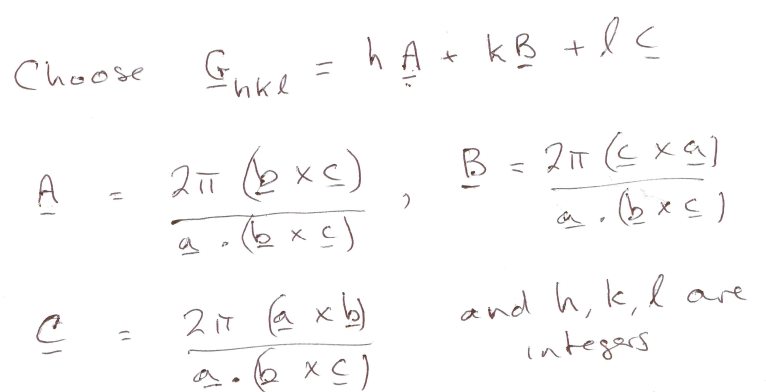
Brillouin Zone

• Wigner-Seitz unit cell for reciprocal lattice

• constructed the same way as actual lattice

• contains values of the wavenumber k

Condition on symmetry of potential describing electron interaction with other electrons and nuclei in a crystal symmetry

must be the same symmetry as the lattice

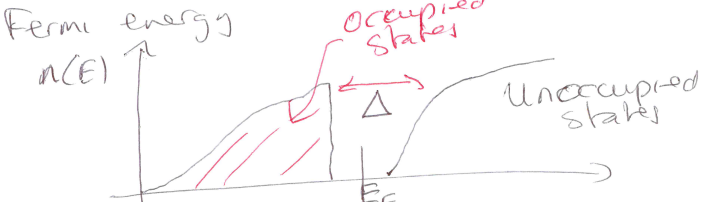
Insulator condition

• energy gaps open up in potential

• if fermi energy lies in a gap, the system is an insulator

• energy gap > 2eV

Bloch theorem

For an electron moving in a periodic potential the Schrödinger wave equation must have solutions of the form \phi_{n,k}\left(\underline{r})=e^{i\underline{k}\cdot\underline{r}}u_{n,k}\left(\underline{r}\right)\right. , where u_{n,k}\left(\underline{r}\right) is a periodic function and e^{i\underline{k}\cdot\underline{r}} is a plane wave

Other insulator material facts

• specific heat has no electronic contribution for k_{B}T<\Delta

• material transparent for \frac{hc}{\lambda}<\Delta

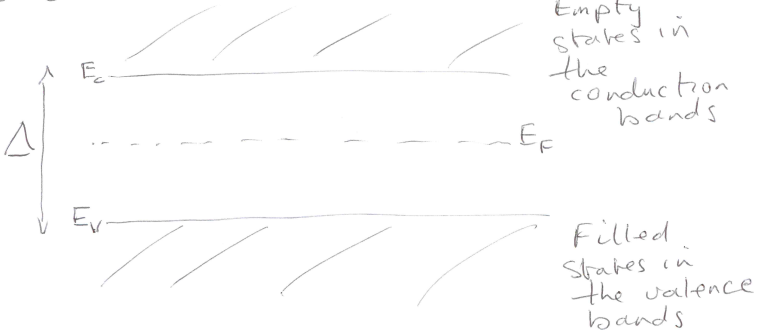
Condition for semi-conductor

\Delta\le2eV

Semiconductor diagram

Semiconductor doping and why it is done

• impurities added to donate 1 electron to conductance band or remove one electron from valence band

• allows for easier conduction

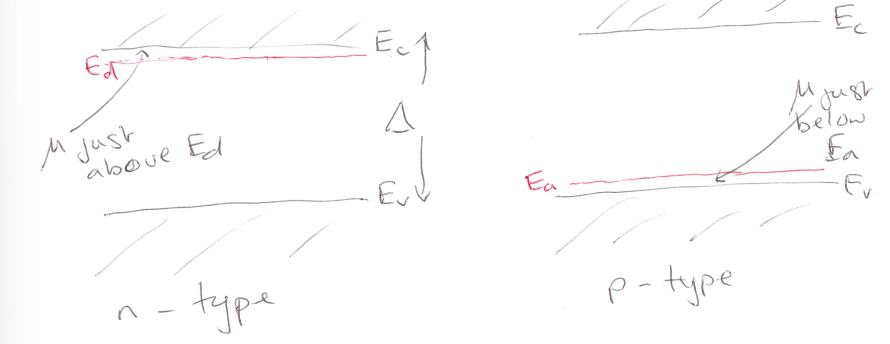
Difference between p-type and n-type semiconductors

• the position of the chemical potential

• in n type, chemical potential just above E_d

• in p type, just below E_a

n-type semiconductors

• majority carriers - electrons

• minority carriers - holes

n-type semiconductors

• majority carriers - holes

• minority carriers - electrons

Current from a p-n junction

I=i_{s}\left(\exp\left(\frac{eV_{applied}}{k_{B}T}\right)-1\right) where

i_{s}=\left\vert i_{pg}\right\vert+\left\vert i_{ng}\right\vert

Current when two materials in p-n junction are in equilibrium

• no net current

• carriers still go back and forth

Set up of electric field in a p-n junction

• holes in p-region diffuse across gap to n-region

• recombine with free electrons

• vice versa for electrons in n-region

What does the potential associated with the p-n junction’s electric field do?

raises energy level in p-region relative to those in n-region so that chemical potentials align

4 currents in p-n junction equilibrium and where they come from

• recombination currents i_pr and i_nr from diffusion process and recombination of electrons and holes

• generation currents i_pg and i_ng from electric field sweeping out electron-hole pairs generated from thermal expansion

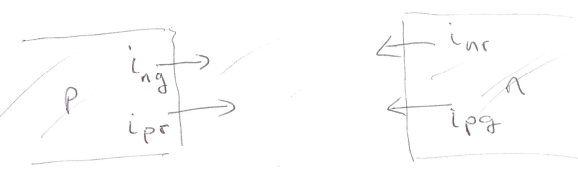
Relationship between the 4 currents in p-n junction equilibrium

i_{pr}+i_{pg}=0

i_{ng}+i_{nr}=0

what is i_ng proportional to?

probability of exciting a minority carrier in p-type region

\exp\left(-\frac{\Delta}{k_{B}T}\right)

what is i_nr proportional to?

probability that a majority carrier has enough energy to surmount the barrier \Delta_{AB}

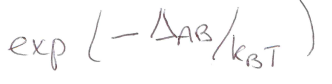
Applying forward bias (positive potential difference) across junction

• decreases electric field

• difference between energy levels in p-region and n-region reduced by \Delta E=-eV_{applied}

• easier for electrons in n-region to diffuse, same for holes in p-region

• both recombination currents increased by factor \exp\left(\frac{eV_{applied}}{k_{B}T}\right)

• generation currents do not change

net hole current in forward bias p-n junction

i_{p,tot}=i_{pr}+i_{pg}=\left\vert i_{pg}\right\vert\left(\exp\left(\frac{eV_{applied}}{k_{B}T}\right)-1\right)

net electron current in forward bias p-n junction

i_{n,tot}=\left\vert i_{ng}\right\vert\left(\exp\left(\frac{eV_{applied}}{k_{B}T}\right)-1\right)

Spin magnetic moment of an electron

• interacts with magnetic field

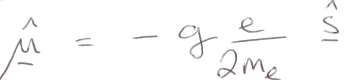
What is the shell model of protons and neutrons analogous to?

It is analogous to how electrons in an atom are modeled, where each nucleon moves in a potential that captures the average effect of all other nucleons.

What additional potential energy do protons experience in the nucleus?

Protons experience an additional potential energy associated with Coulomb repulsion, as each proton interacts with a sphere of uniform charge density of radius R and total charge (Z−1)e.

What does it mean for potentials to be spherically symmetric in the shell model?

If potentials are spherically symmetric, angular momentum l is conserved.

What are the "magic numbers" in nuclear physics?

The "magic numbers" are 2, 8, 20, 28, 50, 82, and 126. Nuclei with these numbers of neutrons or protons are very stable.

In a 1D crystal, where do gaps open up in the energy spectrum?

Gaps open up at k=±nπ/a where electron waves will be diffracted by the lattice

What is the Schrödinger Equation for a free particle?

i\hbar\frac{\partial\Psi}{\partial t}(r,t)=-\frac{\hbar^2}{2m}\nabla^2\Psi(r,t)

What is the relativistic energy-momentum relation?

E^2=p^2c^2+m^2c^4

What is the Klein-Gordon Equation?

The Klein-Gordon equation is derived from the relativistic energy-momentum relation and is a second-order derivative with respect to time, unlike the first-order Schrödinger Equation. It has the form:

-\hbar^2\frac{\partial^2}{\partial t^2}\Psi(r,t)=-\hbar^2c^2\nabla^2\Psi(r,t)+m^2c^4\Psi(r,t)

What problem arises with negative energy solutions in the Klein-Gordon equation?

The probability density \Psi^{\ast}(r,t)\Psi(r,t) is found to be proportional to energy , which is unphysical for negative energy solutions

What was Dirac's key idea to address the issues of relativistic quantum mechanics and negative energy solutions?

Dirac proposed a Hamiltonian linear in momentum and introduced 4×4 matrices (αx​,αy​,αz​,β) to ensure that Hamiltonian gives the relativistic energy-momentum relation. This led to the Dirac Equation.

How many components does the wavefunction in the Dirac Equation have, and what is it called?

The wavefunction Ψ(r,t) in the Dirac Equation has 4 components and is called a Dirac spinor.

What does the Dirac Equation describe?

Fermions

What is the "Dirac Sea" interpretation?

Dirac proposed that all negative energy states are occupied. The Pauli Exclusion Principle then prevents positive energy particles from falling into these filled states.

How are anti-particles explained by the Dirac Sea?

A photon with sufficient energy (E=ℏω>2mc²) can excite an electron from a negative energy state (the Dirac Sea), leaving behind a "hole." This hole corresponds to a positive energy anti-particle with the opposite charge of the particle (e.g., a positron). Particle-antiparticle annihilation also produces photons.

How is the probability of a system being in a particular state calculated in Dirac notation?

If a system is in state

\vert\Psi(t)\rangle=\cos(\Gamma t/\hbar)\vert\downarrow\rangle-i\sin(\Gamma t/\hbar)\vert\uparrow\rangle the probability of being in state ∣↓⟩ is

\cos^2(\Gamma t/\hbar) and in state \vert\uparrow\rangle

is \sin^2(\Gamma t/\hbar)