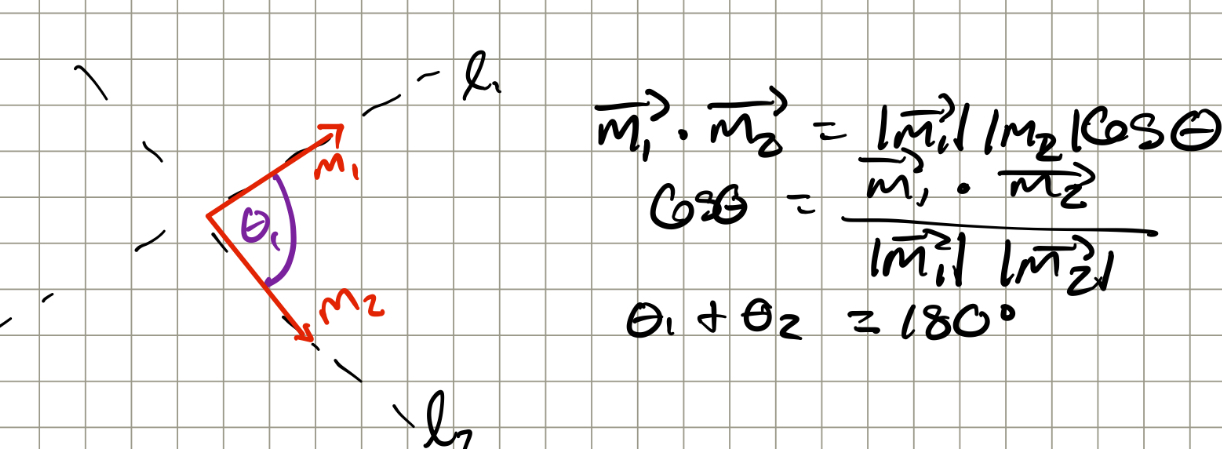8.2 - Cartesian Plane of a Line

Slope y-intercept :

y=mx+b

Point slope :

y-y1 = m(x-x1)

Standard form

Ax+By+C=0

Normal line:

Perpendicular to line

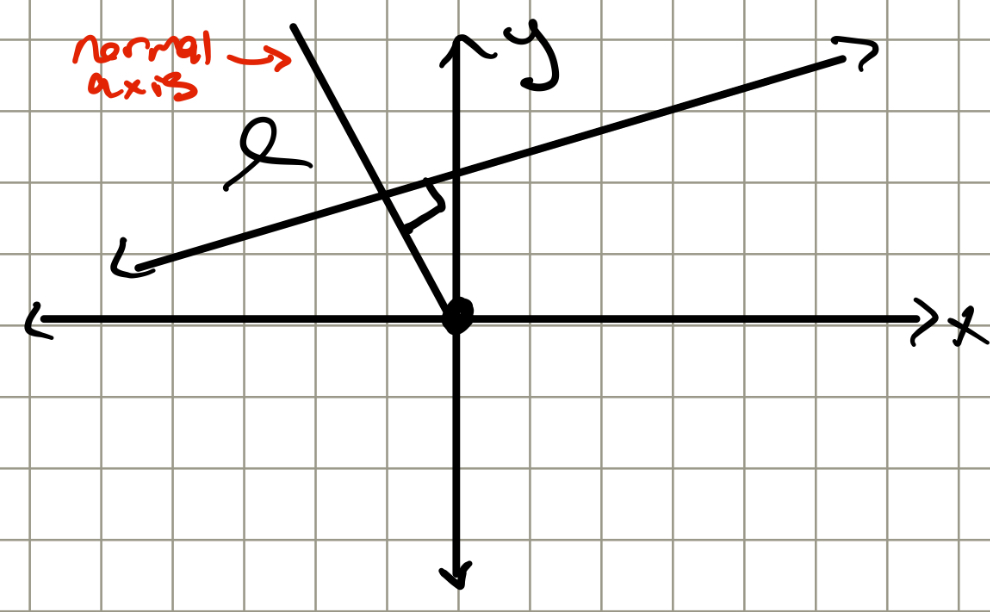
The normal axis:

• For a general line in R² we can draw a line from origin that is perpendicular to that of a general line

• A general point on the normal axis is given by coordinates (A,B)

• A normal vector n = (A,B)

Cartesian equation of a line given by :

Ax +By+C = 0 (standard form) where a normal line to this is (A,B)

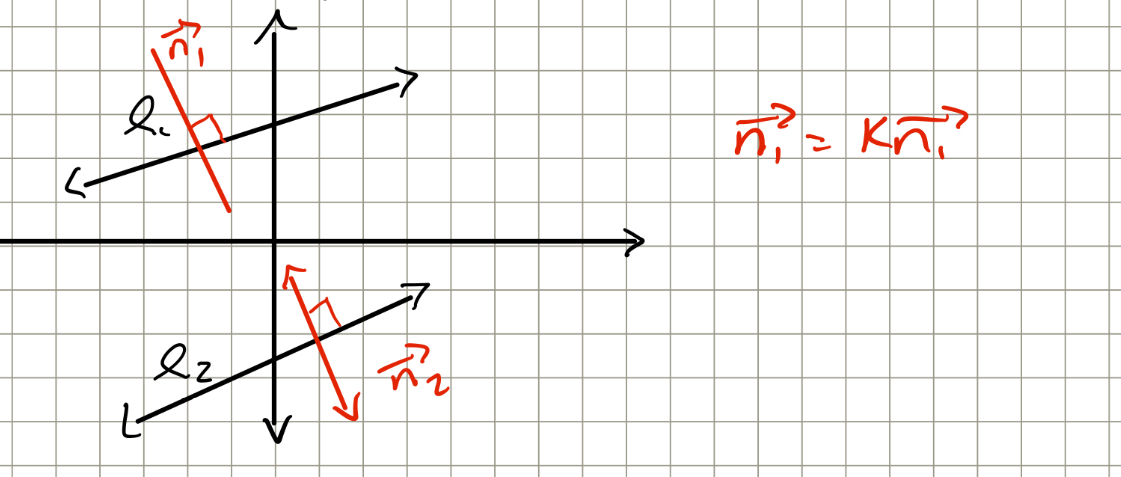
2 lines are parallel if:

their normals are scaler multiples as well as their direction vectors

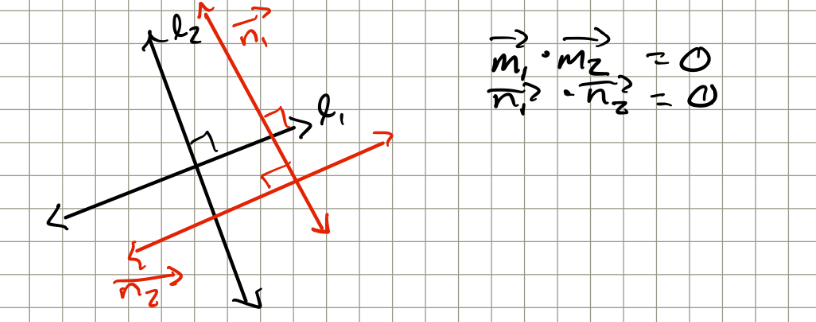
2 lines are perpendicular is

dot product of n1 and n2 is 0 as well as direction vectors

Cartesian equation :

Ax +By + C= 0

Angles between 2 lines are determined :

by finding the angle between 2 direction vectors m1 and m2

Angles found using formula