Algebraic Identities and Fundamentals of Maths

Flashcards made from Maths Unplugged's crash course videos. Suitable for those writing JEE. Answer only with definition (I've included cards for both ways around). There are topics not covered in MU as well, marked.

$$(a+b)²$$

$$a²+b²+2ab$$

$$(a-b)²$$

$$a²+b²-2ab$$

$$a²+b²+2ab$$

$$(a+b)²$$

$$a²+b²-2ab$$

$$(a-b)²$$

$$(a+b)(a-b)$$

$$a²-b²$$

$$a²-b²$$

$$(a+b)(a-b)$$

$$a^{m^n}$$

$$a^{m^n}$$

$$(a^m)^n$$

$$a^{mn}$$

$$(\Sigma a)²$$

$$\Sigma(a²)+2\Sigma(a_1a_2)$$

$$\Sigma(a²)+2\Sigma(a_1a_2)$$

$$(\Sigma a)²$$

$$\Sigma a_1a_2$$

$\dfrac{(\Sigma a)²-\Sigma (a²)}{2}$ 

$\dfrac{(\Sigma a)²-\Sigma (a²)}{2}$ 

$$\Sigma a_1a_2$$

$$\Sigma a_1a_2 = \dfrac{(\Sigma a)²-\Sigma (a²)}{2}$$

How is this derived?

By using identities like $(a+b)²$ and $(a+b+c)²$.

$$(1+a)(1+a²)(1+a^4)(1+a^8)…(1+a^n)$$

$$\dfrac{1-a^{2n}}{1-a}$$

$$\dfrac{1-a^{2n}}{1-a}$$

$$(1+a)(1+a²)(1+a^4)(1+a^8)…(1+a^n)$$

$$\dfrac{1-a^{2n}}{1-a}=(1+a)(1+a²)(1+a^4)(1+a^8)…(1+a^n)$$

How is this derived?

Multiple and divide RHS by $(1-a)$, then you use $(a+b)(a-b)=a²-b²)$ to cancel out all the consecutive terms.

$$(a+b+c)²$$

$$a²+b²+c²+2(ab+bc+ca)$$

$$a²+b²+c²+2(ab+bc+ca)$$

$$(a+b+c)²$$

$$(a+b+c+d)²$$

$$a²+b²+c²+d²+2(ab + ac + ad + bc + bd + cd)$$

$$(a+b)³$$

$$a³+b³+3ab(a+b)$$

$$a³+b³+3ab(a+b)$$

$$(a+b)³$$

$$a²+b²+c²+d²+2(ab + ac + ad + bc + bd + cd)$$

$$(a+b+c+d)²$$

$$a³+b³$$

give both forms of this.

$$(a+b)³-3ab(a+b)$$

$$(a+b)(a²+b²-ab)$$

$$(a+b)³-3ab(a+b)$$

$$a³+b³$$

$$(a+b)(a²+b²-ab)$$

$$a³+b³$$

$$(a-b)³$$

$$a³-b³-3ab(a-b)$$

$$a³-b³-3ab(a-b)$$

$$(a-b)³$$

$$a³-b³$$

give both forms

$$(a-b)³+3ab(a-b)$$

$$(a-b)(a²+b²+ab)$$

$$(a-b)(a²+b²+ab)$$

$$a³-b³$$

$$(a-b)³+3ab(a-b)$$

$$a³-b³$$

$$a²-ab+b²$$

Give all 3 forms

$$(a+b)²-3ab$$

$$(a-b)²+ab$$

$$\dfrac{a³+b³}{(a+b)}$$

$$\dfrac{a³+b³}{(a+b)}$$

$$a²-ab+b²$$

$$a²+ab+b²$$

give all 3 forms

$$(a+b)²-ab$$

$$(a-b)²+3ab$$

$$\dfrac{a³-b³}{a-b}$$

$$\dfrac{a³-b³}{a-b}$$

$$a²+ab+b²$$

$$a^4-b^4$$

$$(a²+b²)(a²-b²)$$

$$a^4+b^4$$

$$(a²+b²)²-2a²b²$$

$$a²+b²$$

$$(a+b)²-2ab$$

$$a^4+4b^4$$

$$(a²+2b²-2ab)(a²+2b²+2ab)$$

derive simply and simplify

$$a^4+a²+1$$

$$(a²+a+1)(a²-a+1)$$

$$(a²+a+1)(a²-a+1)$$

$$a^4+a²+1$$

$$a^8+a^4+1$$

$$(a^4+a²+1)(a^4-a²+1)$$

$$(a^4+a²+1)(a^4-a²+1)$$

$$a^8+a^4+1$$

$$ab+bc+ca$$

$$\Big(\dfrac1a+\dfrac1b+\dfrac1c\Big)abc$$

$$\Big(\dfrac1a+\dfrac1b+\dfrac1c\Big)abc$$

$$ab+bc+ca$$

$$a²+b²+c²$$

$$(a+b+c)²-2(ab+bc+ca)$$

$$(a+b+c)²-2(ab+bc+ca)$$

$$a²+b²+c²$$

$$a³+b³+c³$$

$$(a+b+c)(a²+b²+c²-ab-bc-ca) + 3abc$$

$$(a+b+c)(a²+b²+c²-ab-bc-ca) + 3abc$$

$$a³+b³+c³$$

If $a+b+c=0$, what is $a³+b³+c³=$?

$$a³+b³+c³=3abc$$

if  $a³+b³+c³=3abc$, then what can you infer? (2 things)

either $a+b+c=0$

or $a=b=c$

$$a²+b²+c²-ab-bc-ca$$

Give all 3 forms of this.

$$=\dfrac{1}{2}[(a-b)²+(b-c)²+(c-a)²]$$

$$=(a+b+c)²-3(ab+bc+ca)$$

$$=\dfrac{(a+b+c)³-3abc}{a+b+c}$$

if $a²+b²+c²-ab-bc-ca=0$, what can you infer (2 things)?

that $a³+b³+c³=3abc$

and $(a-b)²+(b-c)²+(c-a)²=0$ which means $a=b=c$

if $a²+b²+c²=0$, what can you infer?

$$a=b=c=0$$

$$(a²-b²)³+(b²-c²)³+(c²-a²)³=?$$

How do you derive this?

$$3\left(a^2-b^2\right)\left(b^2-c^2\right)\left(c^2-a^2\right)$$

This is like $X³+Y³+Z³$.

Since $X+Y+Z=0$, then $X³+Y³+Z³=3XYZ$.

What can you infer from $(x-a)²+(y-b)²+(z-c)³=0$?

$$x=a,y=b,z=c$$

What can you infer from $(x-a)²+(x-b)²+(x-c)³=0$?

$$a=b=c$$

if not, the equation cannot exist

$$abc+(ab+bc+ca)+(a+b+c)+1$$

$$(a+1)(b+1)(c+1)$$

$$(a+1)(b+1)(c+1)$$

$$abc+(ab+bc+ca)+(a+b+c)+1$$

$$abcd+(a+b+c+d)+(ab+ac+ad+bc+bd+cd)+(abc+abd+acd+bcd)+1$$

$$(a+1)(b+1)(c+1)(d+1)$$

$$(a_1+1)(a_2+1)(a_3+1)+…+(a_n+1)$$

$$1 + \Sigma a_1 +\Sigma (a_1a_2)+\Sigma (a_1a_2a_3)+…+(a_1a_2a_3…a_n)$$

$$1 + \Sigma a_1 +\Sigma (a_1a_2)+\Sigma (a_1a_2a_3)+…+(a_1a_2a_3…a_n)$$

$$(a_1+1)(a_2+1)(a_3+1)+…+(a_n+1)$$

$$(a+b+c)³$$

$$a³+b³+c³+3(a+b)(b+c)(c+a)$$

$$a³+b³+c³+3(a+b)(b+c)(c+a)$$

$$(a+b+c)³$$

$$(a+b+c)³=a³+b³+c³+3(a+b)(b+c)(c+a)$$

How do you derive this?

consider $X=a+b$ and $Y=c$ and solve $(X+Y)³$.

$$(a-b+c+d)(a+b-c+d)(a+b+c-d)(b+c+d-a)$$

How do you approach this?

$$(a+b+c+d-2b)(a+b+c+d-2c)(a+b+d+c-2d)(a+b+c+d-2a)$$

Let $a+b+c+d=x)$

then,

$=(x-2a)(x-2b)(x-2c)(x-2d)$.

Not from MU

Every prime number greater than 3 is in the form of _____, but the converse need not be true.

$$6k\pm1$$

Not from MU

When given a question where a variable is a prime number, what can you do? Just like what is the first thing that should pop into your head?

Can factorise it, and the factors are always going to be 1 and itself.

Not from MU

If $f(x)$  is divided by $ax-b$ . what form will the remainder be in?

$$mx+n$$

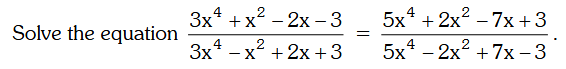
Not from MU

How would you approach this question?

Group some terms, it looks like componendo dividendo, apply that.

Not from MU

What is the relation between $|a+b|$ and $|a|+|b|$?

$$|a+b|\le|a|+|b|$$

Not from MU

What is the relation between $|a-b|$ and $|a|-|b|$ ?

$$|a-b|\ge|a|-|b|$$

Not from MU

What are the limitations of logarithms? $\log_aN$

(three limitations)

1. $$a>0$$

2. $$N>0$$

3. $$a\ne 1$$

What is $\log_{a^m}b^n$ ?

$$\dfrac{n}{m}\log_ab$$

What is $\log_x a + \log_x b$?

$\log_x ab$  

What is $\log_x a - \log_x b$ ?

$\log_x \dfrac{a}{b}$ 

What is $\log_aa=$?

$$1$$

What is $\log_a1=$?

$$0$$

What is $\dfrac{\log_ab}{\log_ac}=$?

$$\log_cb$$

What is $a^{\log_ac}=$?

$$c$$

What is $a^{\log_bc}=$?

$c^{\log_ba}$ 

If in $\log_ab$, both $a$ and $b$ are on the same side of $1$ (on the number line), then will the value of log be negative or positive?

positive

If in $\log_ab$, both $a$ and $b$ are on different sides of $1$ (on the number line), then will the value of log be negative or positive?

negative

Under what conditions will $\log_ab>1$ be true?

if $b>a$ and $a>1$.

Not from MU

What is $\log_ea$ in terms of $\log$ to the base $10$?

$$\log_ea=2.303\times\log_{10}a$$

Not from MU

What is $\dfrac{1}{\log_ab}$?

$\log_ba$ 

Not from MU

What is $\log_{10}a$ in terms of $\log$ to the base $e$?

$\log_{10}a=0.434\times\log_ea$ 

Not from MU

What does the graph for $y=\log_ax$ look like when $a>1$?

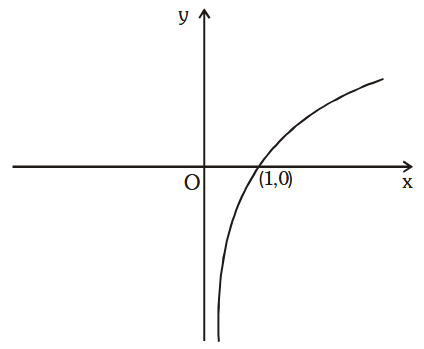
Not from MU

What does the graph for $y=\log_ax$ look like when $a<1$?

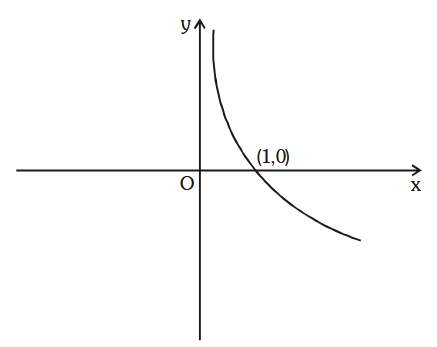
Not from MU

If $\log_ax < \log_ay$, when is $x>y$? When is $x<y$?

$x<y$ when $a>1$

$x>y$ when $a<1$

Not from MU

when is $x+\dfrac1x\ge2$?

when $x$ is a positive real number

Not from MU

When is $x+\dfrac1x\le2$?

when $x$ is a negativ real number

Not from MU

What is the approximate value of $\log_{10}2$?

$$0.3010$$

Not from MU

What is the approximate value of $\log_{10}3$?

$$0.4771$$

Not from MU

What is the approximate value of $\log_{e}2$?

$$0.693$$

Not from MU

What is the approximate value of $\log_{e}10$?

$$2.303$$

Not from MU

if $\log_ax>p$, what happens when $a>1$?

$$x>a^p$$

Not from MU

if $\log_ax>p$, what happens when $0<a<1$?

$$0<x<a^p$$