Populationsökologie

Definition Populationsökologie

Lehre von der Population (= Bevölkerung), ihrer Struktur- und Funktionsmerkmale und ihrer Dynamik

Population homotypisch

= Population im engeren Sinne: Gesamtheit der Individuen einer Art, die einen zusammenhängenden Bereich bewohnen und dort in Wechselwirkung treten (im Allgemeinen durch mehrere Generationen genetische Kontinuität zeigen)

Population heterotypisch

Individuenmenge, die aus mehreren Arten besteht

was ist ein unitarer Organismus

Organismus, der in seiner vorgegebenen Entwicklung zu einer spezifischen Adultform führt (fast alle Tierarten)

was ist ein modularer Organismus

Organismus, der aus physiologisch mehr oder weniger unabhängigen Funktionseinheiten (Module) bestehen kann, die weitere klonale Kopien (sog. Ramets) produzieren können und zusammen einen Genet darstellen → Solche Organismen sind in der Regel sessil (Z.B. Moostierchen)

Ideale Eigenschaften einer Population, in der man alle Individuen zählen kann

→ p_est = 1

o   Distinkte Individuen (=unitarer Organismus)

o   Große Individuen

o   Individuen nicht mobil

o   Geringe Populationsgröße

o   Erfassungsfreundliche Umgebung

o   Kleine geografische Verbreitung

allgemeine Formel Populationsgrößenschätzungen unitarer Organismen

Populationsgrößenschätzung modularer Organismen allgemein

durch Schwierigkeiten, Individuen modularer Organismen voneinander abzugrenzen, werden häufig andere Größen als bei unitaren Organismen bestimmt, um bei modularen Organismen zumindest Populationsgrößenveränderungen abschätzen zu können (z.B. Biomasse oder Deckungsgrad anstatt Anzahl Individuen)

warum sollte bei der Populationsgrößenbestimmung durch Zählung von Individuen auf zufälligen Flächen des Habitates mehrere Teilflächen untersucht werden?

• Berücksichtigung der Unterschiede in der Individuenverteilung

• Daten von mehreren Stichproben erlauben auch den Schätzfehler bei der Populationsgrößenabschätzung zu bestimmen

was sollte man bei der Bestimmung der Größe eines Teilgebiets eines Habitats zur Populationsgrößenbestimmung beachten

→ Größe der beprobten Teilflächen zur Populationsgrößenbestimmung muss sich an Eigenschaften der untersuchten Arten orientieren

o   Z.B. korreliert Individuendichte i. d. R. negativ mit dem Gewicht der Individuen (je höher Gewicht desto kleiner Populationsdichte)

o   Z.B. oft je größer die Individuen einer Tierart, desto größer Ausbreitungsgebiet

Prinzp der Fang-Wiederfang.Methode zur Populationsgrößenabschätzung

Individuen im Probegebiet werden gefangen, die gefangenen markiert und wieder freigelassen. Fangen von Individuen wird wiederholt, dabei sieht man wie viele der Tiere schon einmal gefangen hatte (sind ja markiert) -> man kann dann hochrechnen, wie groß Population wahrscheinlich ist

Gleichung Fang-Wiederfang-Methode

wann findet Fang-Wiederfang-Methode Anwendung?

Findet Anwendung, wenn nur ein Teil der Tiere auf einer Probefläche erfasst werden kann

>       mobile, schwer zählbare Tieren

>       daher auch nicht geeignet für modulare Organismen

welche Annahmen/Bedingungen müssen bei der F-W-Methode gelten, damit sie zuverlässig ist

1.      Die Population ist geschlossen (während Untersuchung keine Geburten, Sterbefälle, Ein- und Auswanderung)

2.      Individuen bleiben durch Markierung unbeeinflusst

was ist die Akkumulationskurve bei der Populationsgrößenbestimmung und wann wendet man sie an

→   wichtiges Werkzeug zur Überprüfung, ob Datengrundlage ausreichend ist, um verlässliche Populationsschätzungen durchzuführen

>       Wie viel zusätzliche Tiere erfasse ich, wenn ich die Stichprobe vergrößere?

→ wenn Kurve abflacht, kannst man Populationsgrößen realistisch hochrechnen

 

·        Anwendung z. B. bei DNA-Analysen, die die Anwesenheit von spezifischen Individuen (auch) indirekt zu erfassen versuchen (z. B. durch Untersuchung von Kot, Haaren, Federn)

·        DNA-Analysen finden v. a. Anwendung, wenn Arten extrem scheu sind (z. B. Auerhuhn, Luchs, Wolf)  -> schwer zu erfassende Tiere

welche Faktoren beeinflussen die Populationsgrößenentwicklung

Fortpflanzungs- und Sterberate, Migration, Abwanderung

diskontinuierlicher Lebenszyklus

zeitlich klar abgegrenzte Fortpflanzungsereignisse (z.B saisonal bedingt)

kontinuierlicher Lebenszyklus

Fortpflanzung findet ständig statt, nicht nur zu bestimmten Jahreszeiten oder in klar definierten Zeiträumen

Fundamentale Gleichung der Populationsgrößen-Entwicklung

 

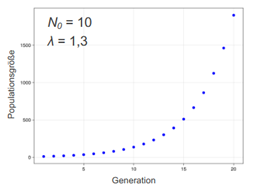
Populationsgrößenentwicklung einer sich diskontinuierlich reproduzierenden Art wenn Sterbe- und Geburtenrate konstant (unabhängig von Populationsgröße immer gleich)

→ Populationsgrößenentwicklung ist geometrisch (diskrete Version von exponentiell -> zwischen den Generationen ist Größe ja konstant, daher nicht tatsächlich exponentiell → sprunghaft)               

• Keine Zu- und Abwanderung

• Geburten- und Sterberate konstant -> ungebremstes Wachstum

• Je mehr Individuen in Population, umso mehr Individuen werden geboren und umso mehr Individuen sterben in einem gegebenen Zeitfenster  

       → Wachstumsfaktor konstant      

N_g = N₀ * lamda^g            

g = Anzahl der verstrichenen Generationen         

lamda = N_g+1 / N_g                                            

Populationsgrößenentwicklung einer sich kontinuierlich reproduzierenden Art wenn Sterbe- und Geburtenrate konstant (unabhängig von Populationsgröße immer gleich)

→   Populationsgröße entwickelt sich exponentiell

• Keine Zu- und Abwanderung

• Geburten- und Sterberate konstant -> ungebremstes Wachstum

»   Je mehr Individuen in Population, umso mehr Individuen werden geboren und umso mehr Individuen sterben in einem gegebenen Zeitfenster

Populationsgröße zum Zeitpunkt t: N_t = N₀ * e^rt

r = (g-s) -> spezifische Wachstumsrate

g = durchschnittliche Geburtenrate pro Individuum pro Zeiteinheit dt

s = durchschnittliche Sterberate pro Individuum pro Zeiteinheit dt

wie ergibt dich die gleichung für die Bestimmung der Populationsgröße zum Zeitpunkt t einer sich kontinuierlich fortpflanzenden Art bei konstanter Sterbe- und Geburtenrate

Populationsgröße zum Zeitpunkt t: N_t = N₀ * e^rt

r = (g-s) -> spezifische Wachstumsrate

g = durchschnittliche Geburtenrate pro Individuum pro Zeiteinheit dt

s = durchschnittliche Sterberate pro Individuum pro Zeiteinheit dt

→   Formel ergibt sich aus Populationsgrößenänderung dN/dt

»   Da die Population kontinuierlich wächst, muss Populationsgrößenänderung innerhalb eines extrem kleinen Zeitintervals dt (lim -> 0) bestimmt werden

o   Geburten = N * g (mit g = durchschnittliche Geburtenrate pro Individuum pro Zeiteinheit dt)

o   Todesfälle = N * s (mit s = durchschnittliche Sterberate pro Individuum pro Zeiteinheit dt)

→   durch Lösen der Differentialgleichung dN/dt mit dt -> 0 (wegen den möglichst kleinen Intervallen) ergibt sich dann Gleichung für N_t

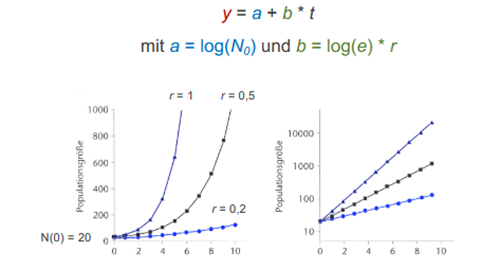
lineare Darstellung Exponentieller Wachstumskurven

Durch halblogarithmische Darstellung wird exponentielles Wachstum linearisiert

→ Wenn durch Halblogarithmisierung keine Gerade entsteht ist Wachstum nicht exponentiell

Zeit für Verdopplung der Populationsgröße einer exponentiell wachsenden Population

Zeit für Verdopplung nur abhängig von r, unabhängig von N₀

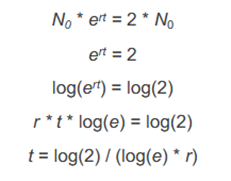
warum ist Annahme einer unveränderlichen spezifischen Zuwachsrate r = (g – s) unrealistisch

Mit steigender Populationsgröße werden Ressourcen knapper, und es sollten weniger Geburten und mehr Sterbefälle auftreten -> sinkende Zuwachsrate bei zunehmender Populationsgröße

→ Geburten- und Sterberate sind dichtereguliert

spezifische Zuwachsrate r einer sich kontinuierlich fortpflanzenden Art, wenn Geburten- und Sterberate dichtereguliert sind

• r ist Abhängig von Populationsgröße N → r_N

• r_N ist maximal bei N=0 (noch keine Ressourcen verbraucht)

• r = 0 bei N = K

was ist die Kapazitätsgrenze K

→ Populationsgröße am Schnittpunkt von Geburten- und Sterberate

·       Realistisch eher ein Wertebereich

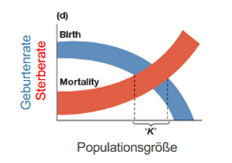
spezifische Zuwachsrate einer sich kontinuierlich Fortpflanzenden Art bei dichteregulierter Sterbe- und Geburtenrate

r_N = r_m -  r_m * (N/K)                                

mit r_m = maximal spez. Zuwachsrate (N=0)

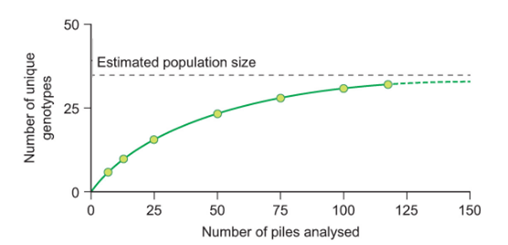
Gleichung Populationsgröße zum Zeitpunkt t einer sich kontinuierlich fortpflanzenden Art bei dichteregulierter Sterbe- und Geburtenrate und wie groß kann Nt maximal werden

Nt ist maximal am Punkt N = K

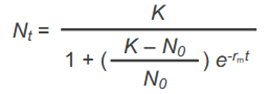
Populationsgrößenentwicklung einer sich kontinuierlich reproduzierenden Art bei dichteregulierter Sterbe- und Geburtenrate

→   Populationsgröße hat S-förmigen Graphen  -> typische logistische Wachstumskurve

Populationsgröße pendelt sich um K ein und bleibt dort dann stabil

>       K wird ja erreicht, weil durch steigende Individuenzahl weniger Ressourcen pro Individuum da sind wodurch Geburtenrate sinkt und/oder Sterberate steigt. Wenn K erreicht ist überwiegt Sterberate. Dadurch werden es wieder weniger Individuen, heißt mehr Ressourcen pro Individuum wieder und wieder steigende Geburtenrate -> Zustand pendelt sich um K ein

was ist der Alle’-Effekt

→   Population hat bei sehr kleiner Populationsgröße Schwierigkeiten zu Wachsen bzw. überhaupt zu überleben (negative Wachstumsrate unterhalb einer bestimmten Populationsgröße)

>       bestimmte positive Faktoren fehlen, die bei größeren Populationen vorhanden sind

mögliche Faktoren:

o   Probleme bei Partnerfindung

o   Probleme bei Jagd in zu kleinem Rudel

o   Fehlen sozialer Interaktionen

→ Erklärt, warum die Population einiger in der Vergangenheit fast bis zur Ausrottung gejagten Arten nach vollständigem Schutz dennoch nicht rasch wieder wachsen (Bsp: Atlantischer Nodkaper)

Lebenszyklusstrategien

r-Strategen und K-Strategen

was sind r- und was K-Strategen

was sind iteropare Arten

Arten, die während ihrer Lebenszeit zwei oder mehr Reproduktionsphasen haben

(-> meist langlebige Arten)

was sind semelpare Arten

Arten, deren Individuen sich im Laufe ihres Lebens nur einmal fortpflanzen

(-> meist kurzlebige Arten)

was ist die life-history-Theorie

→   Arten unterscheiden sich darin, wie sie (begrenzt verfügbare) Ressourcen innerhalb der individuellen Lebenszeit einsetzen

Beispiele:

• Begrenzte Ressourcen in eigenes Wachstum (-> Überlebenschancen erhöhen wodurch auch Reproduktion über viele Jahre möglich wäre) oder begrenzte Ressourcen eher in den Nachwuchs stecken

• Produktion vieler kleiner oder weniger großer Nachkommen

>       Viele große geht nicht: Ressourcen nur begrenzt verfügbar

• Kosten hoher Reproduktion:

o   Geringeres Wachstum

o   Geringere Überlebenschancen der Eltern

o   Schlechtere Körperinstitution der Nachkommen

»   Konflikt zwischen Wachstum und Reproduktion

 

was sind Lebenstafeln und welche Arten gibt es

→   Übersicht alterspezifischer Mortalitäts- und Fruchtbarkeitsraten (Fekunditätsrate)

• Werden zur Berechnung von Überlebenskurven benötigt

Statistische Lebenstafeln:

• Alle Angaben beziehen sich auf Querschnitt durch die Population zu bestimmter Zeitperiode

• nehmen zeitlich konstante Geburten- und Sterberaten an! Die Annahmen treffen aber eventuell nicht zu

Kohorten-Lebenstafeln:

• Abfolge der Mortalität und der Fekundität einer Gruppe von Individuen (einer Kohorte) wird bis zum Tod des letzten Individuums verfolgt

Gründe für Erhöhtes Aussterberisiko kleiner Populationen

• Demographische Faktoren: Nicht jedes Individuum einer Population pflanzt sich fort (z. B. sehr junge und sehr alte Individuen)

• Genetische Faktoren: Drift (Verlust an Variation, Fixierung abträglicher Allele), Inzucht (-> erhöhtes Risiko der Homozygotie abträglicher Allele), reduziertes Immunabwehrpotential wegen geringer genetischer Vielfalt

• Veränderlichkeit der Umwelt: Epidemien, Schlechtwetterperioden, hoher Räuberdruck, Naturkatastrophen können eher alle Tiere gleichzeitig betreffen, weil es so wenige sind

was sind Metapopulationen

→   Verbund von Teilpopulationen derselben Art, die in voneinander getrennten Lebensräumen (Habitatinseln) leben, aber durch gelegentlichen Individuen-Austausch (z. B. durch Wanderung) verbunden sind

·       Absicherungseffekt: lokales Aussterben -> Wiederbesiedlung

·       Arten, die solche ausbilden wollen, sollten der r-Lebenszyklus-Strategie folgen

>       da sie besser mit Aussterbe-Kolonisierungs-Dynamiken klarkommen: schnell, mobil, zahlreich

Formel Populationsgrößenänderung einer dichteregulierten sich kontiniuierlich reproduzierenden Art

ergibt sich durch Einsetzen von rm in dN/dt = r*N