Studied by 0 peopleGravitational Force (Fg)
the force of attraction between any two masses
Fg = G(m1m2)/r2
G = gravitational constant → 6.67 * 10-11 Nm2/kg2
gravitational field (g)
The area of influence of an object
g = acceleration due to gravity; on earth this is 9.8 m/s2
g = (Gm)/r2
Gravitational Force of Spheres
With a solid sphere, Fg is proportional to r when the mass is INSIDE the sphere
With a hollow sphere, the mass is concentrated at the surface. Anywhere inside it the gravitational force is ZERO.
With a solid OR hollow sphere, Fg is proportional to 1/r2 when the mass is OUTSIDE the sphere
Relationship between orbital radii and velocities
can be found using the conservation of angular momentum
L1 = L2 | Conservation of Angular Momentum |
L = Iω = (mr2)(v/r) | Angular Momentum (L) = Moment of Interia (I) times Angular speed ()
|
I1ω1 = I2ω2 → (mr12)(v1/r1) = (mr22)(v2/r2) | Conservation of Angular Momentum (substituted) |
r1v1 = r2v2 | Relationship between orbital radii and velocities |
Kepler’s Three Laws
Scientific laws that describe the motion of planets around the sun
Law of Orbits, Law of Areas, & Law of Periods
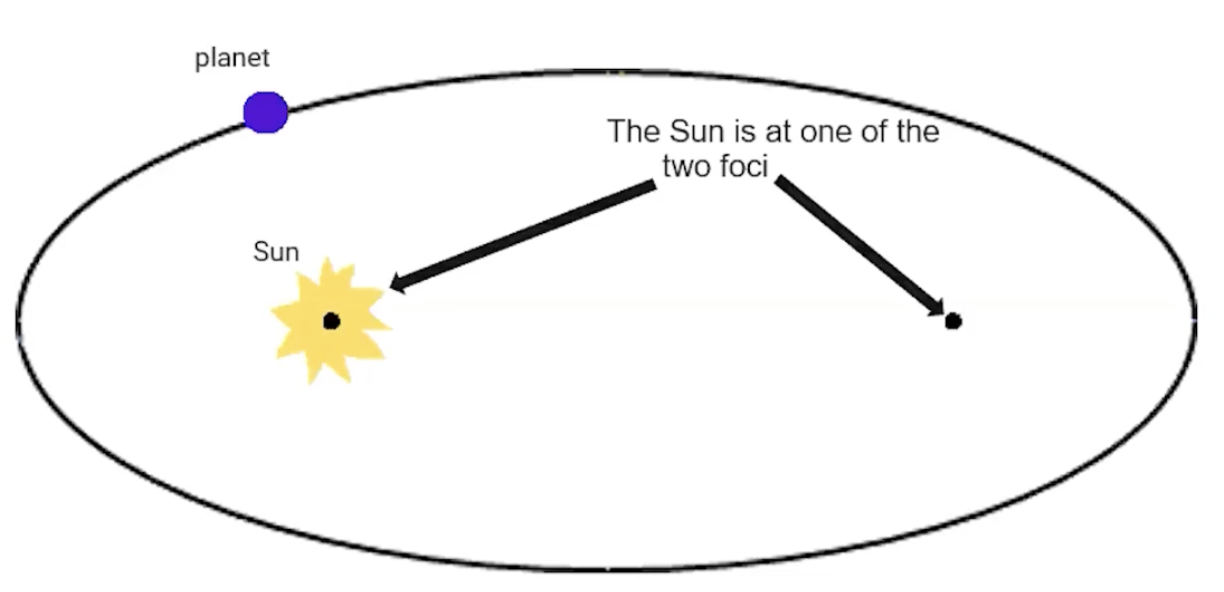
Kepler’s First Law - Law of Orbits
The orbits of the planets are ellipsis, with the sun at one focus
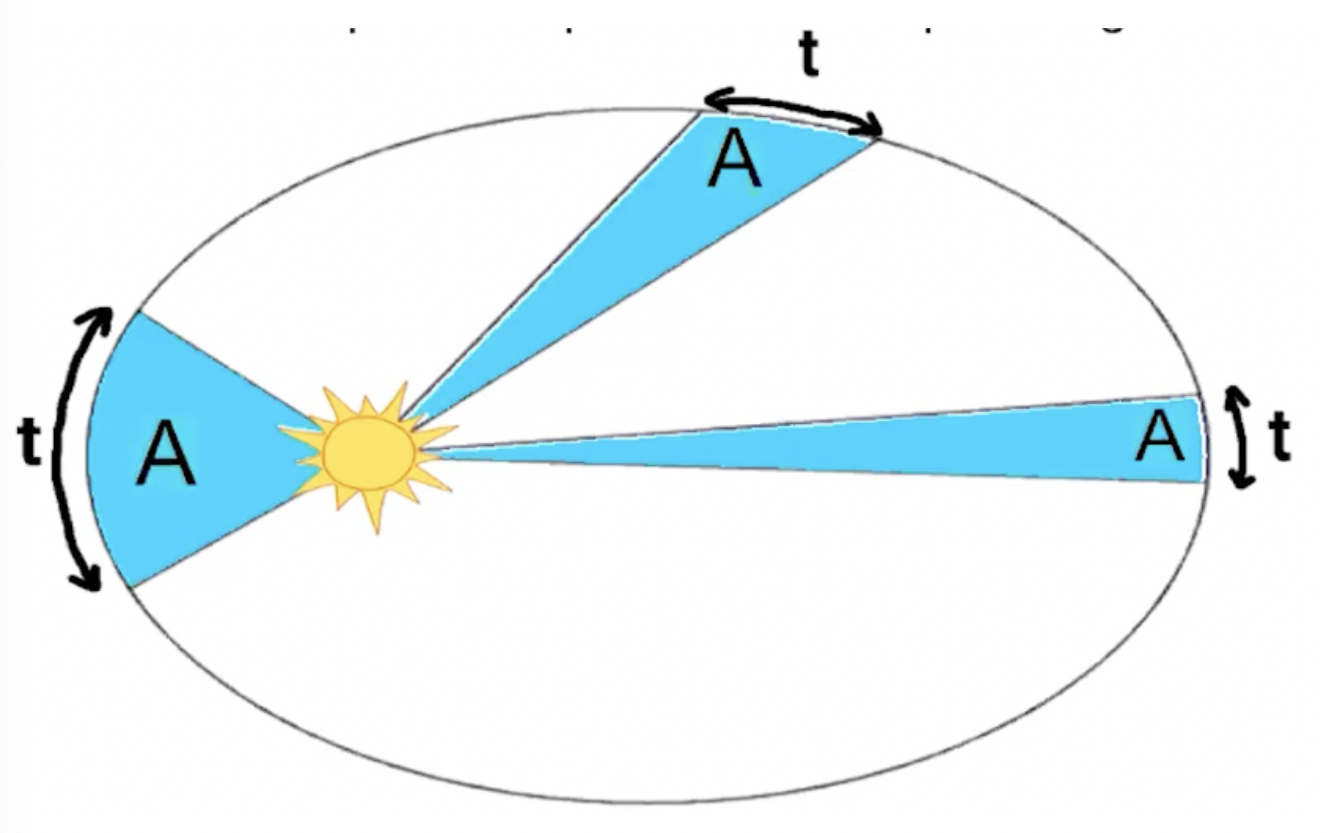
Kepler’s Second Law - Law of Areas
A radius vector joining any planet to the Sun sweeps out equal areas in equal lengths of time
Basically, if the area of the sector is equal the length of time it takes for the planet to travel that length of the circumference is equal
Explained by the conservation of angular momentum: When the planet is closer to the sun, it moves faster.
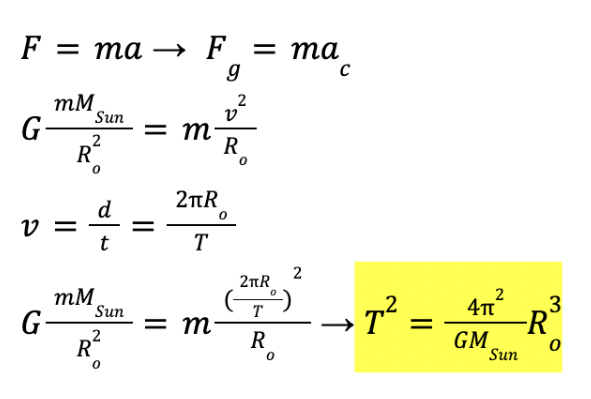
Kepler’s Third Law - Law of Periods
The ratio of the squares of the periods of revolution around the Sun of any two planets equal the ratio of the cubes of the semimajor axes of their respective orbital ellipses → T2 proportional to R3
escape velocity
the velocity needed to escape a planet’s gravitational field
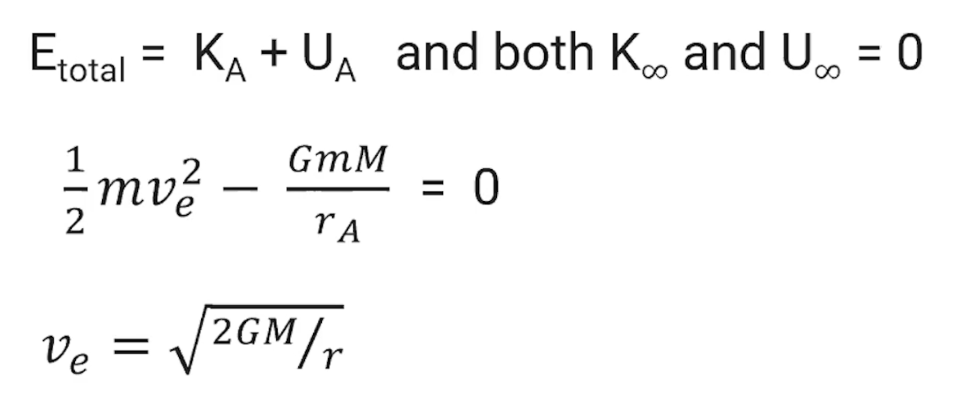
Simple Harmonic Motion
regular repeating motion where the acceleration is proportional to the displacement
EX: a mass on a spring or a pendulum
The object will oscillate between the highest position and the lowest position; the graph looks like a sine graph
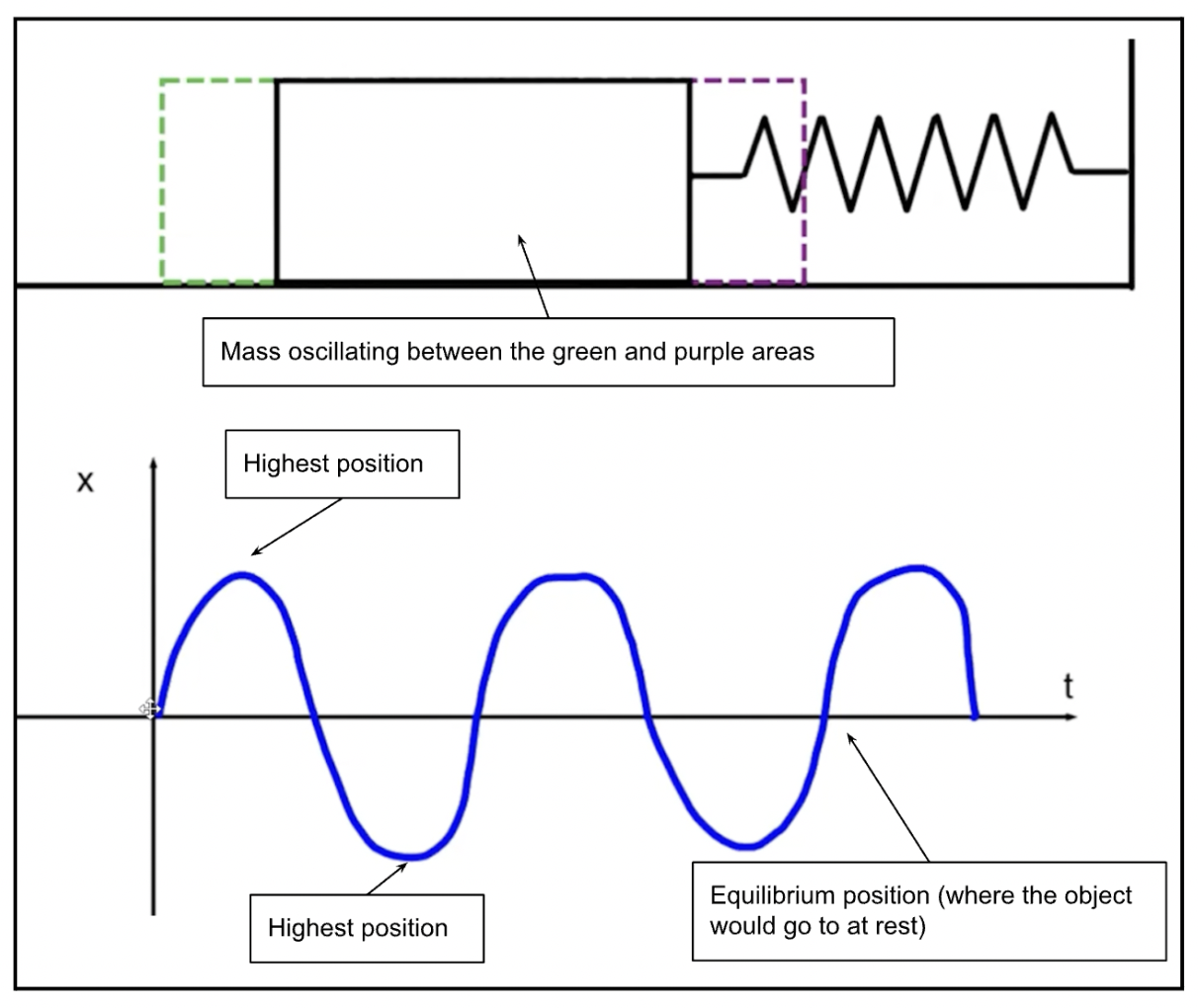
Amplitude (A)
distance from equilibrium to the maximum displacement (on either side)
in the pic, the distance from where the block currently is to the green/purple lines
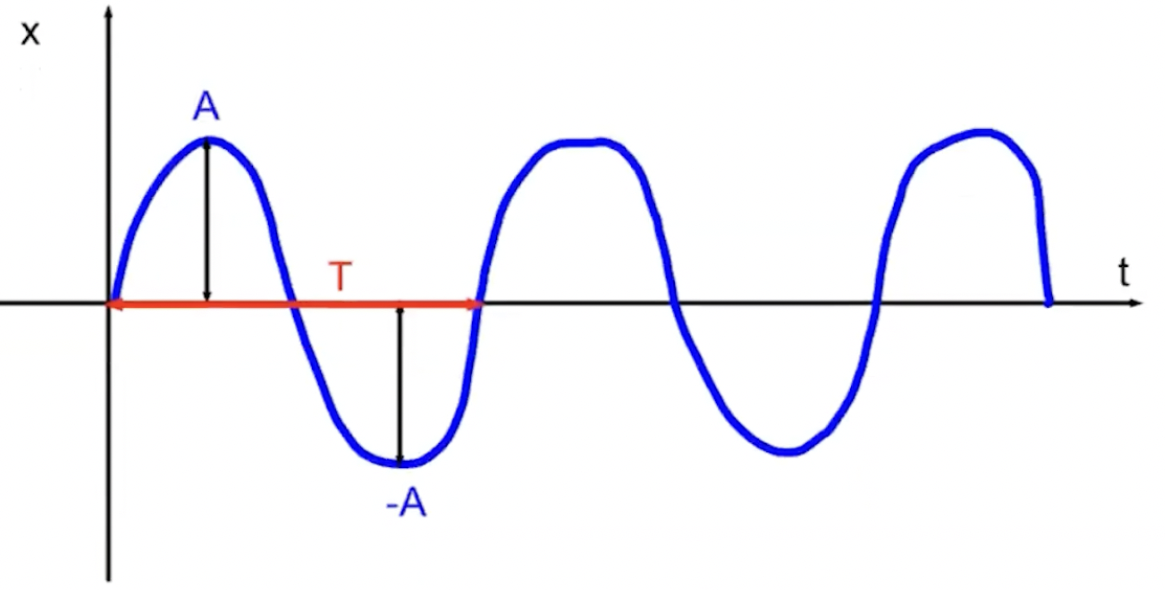
Period (T)
time for one complete oscillation
T = 2π/ω
T = 2π√m/k —> for a spring
T = 2π√L/g —> for a simple pendulum or physical pendulum where < 15o
T = 2π√I/mgD —> for a physical pendulum
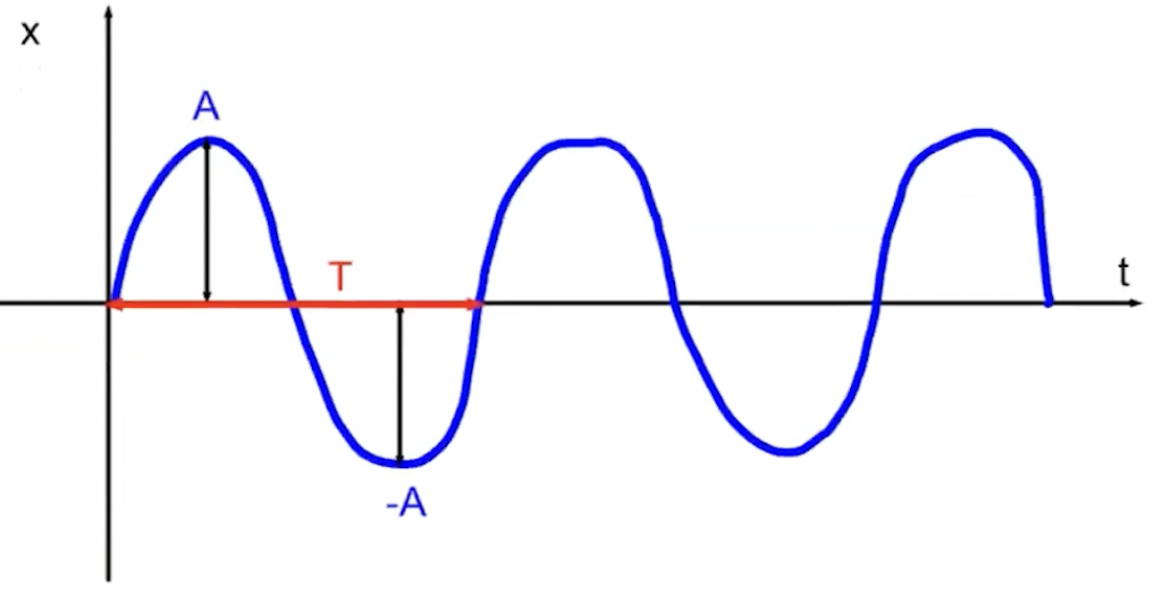
Angular Frequency (ω)
ω = 2π/T
General Equation for a Simple Harmonic Oscillator
position: x(t) = A*sin(ωt)
velocity: v(t) = d/dt [x(t)] = Aω * cos(ωt)
acceleration: a(t) = d2/dt2 [x(t)] = d/dt [v(t)] = -Aω2 * sin(ωt)
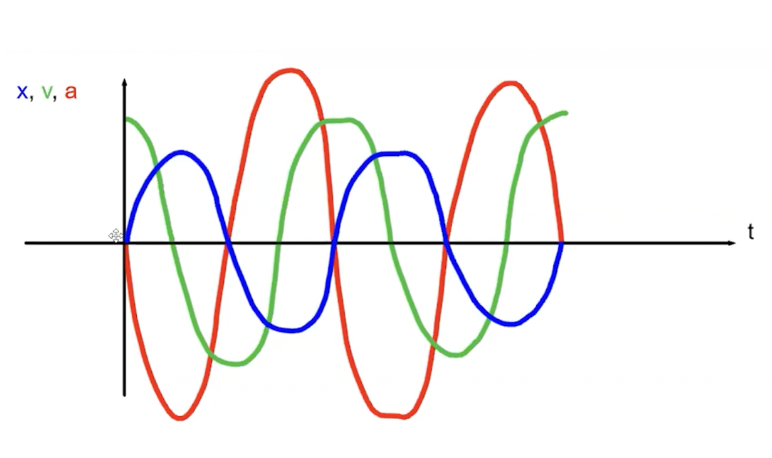
Simple Harmonic Oscillator Graphs - Things to Note
when x(t) is at a maximum, a(t) is at a minimum
x(t) = 0 when a(t) = 0, but v(t) is at a max/min
when x(t) = 0, a(t) = 0 —> when the mass returns to equilibrium position it has no acceleration → no force pulling on you at that point
Velocity is maximum/minimum at equilibrium, x(t) = 0
As you move away from equilibrium (displacement, x, increases) force (and thus acceleration) increases & pulls you back to equilibrium
How to find the equilibrium position of a spring
Moving the system from a horizontal to a vertical position → the spring will naturally stretch (due to gravity) and reach a new equilibrium position, which can be found:
Fnet = kx - mg
Fnet = 0
x = mg/k
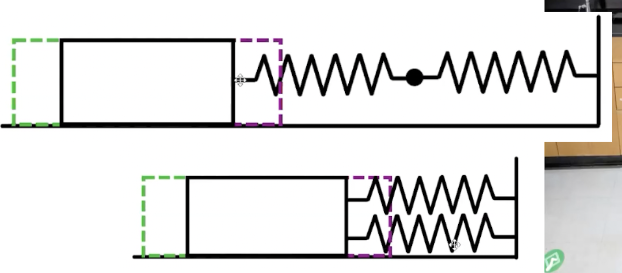
Springs in Combination
the effective spring constant changes
Two springs in series (top) → The springs stretch about twice as much as one spring
1/Keff = 1/K1 + 1/K2 …
Two springs in parallel (bottom) → The springs stretch out half as much as one spring
Keff = K1 + K2 …
if the spring constant is halved, the period doubles → the smaller k gets, the larger the period is
the larger the spring constant the less it stretches; the less it stretches the shorter the period; oscillations happen faster
Pendula
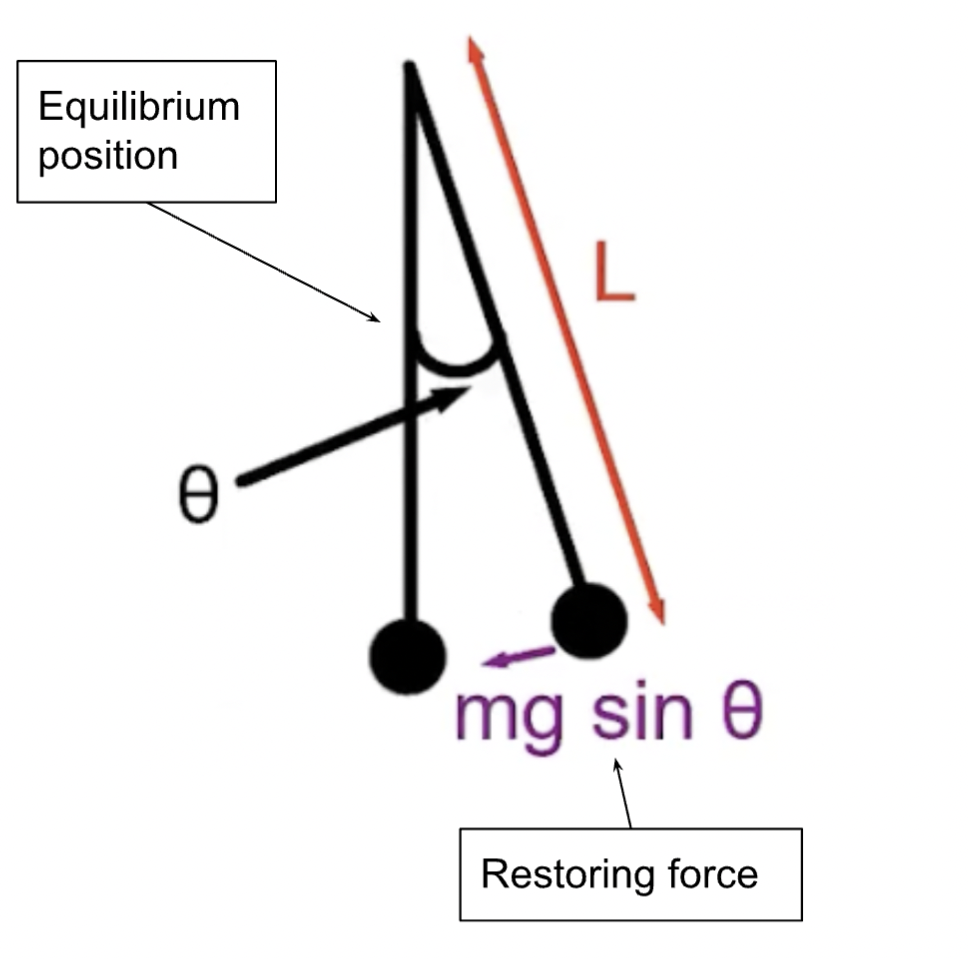
A pendulum demonstrates simple harmonic motion by swinging back and forth
there are three types - simple, physical, and torsional pendulums
In a simple and physical pendulum, gravity provides the restoring force (the force that pulls the pendulum back to its equilibrium position)
Arc Length & Acceleration (Pendulum)
s = Lθ
ds/dt = Lθ * dθ/dt
a = d2s/dt2 = L * d2θ/dt2
Period (T)
T = 2π/ω
Spring: T = 2π√m/k
Simple Pendulum: T = 2π√L/g → simple or physical pendulum where < 15o
NOTE: Orientation does not affect the period of oscillation of the spring-block system → incline/angle doesn’t matter, time stays the same
Period of a Physical Pendulum
T = 2π√I/mgD
I = rotational inertia & D = diameter of the disk
Calculate I using the parallel axis theorem
Period of a Torsional Pendulum
T = 2π√I/
I = rotational inertia of the object around the point that it’s rotation (the center)
= torsional constant → twisting restoring force
Energy of a Spring
for any point in it’s motion: U = ½ * kx2 & K = ½ mv2 → substitute x(t), v(t) in
U = ½ kA2 sin2(ωt)
KE = ½ m(Aω)2 cos2(ωt)
Etot = U + K = ½ kA2
total energy in simple harmonic motion is CONSTANT; energy is transferred between PE and KE
At its extremes, the object has 0 velocities (remember that x(t) max/min is when v(t) = 0) → thus all the energy must be (elastic) potential energy
At equilibrium, x(t) = 0 → thus all energy must be kinetic energy (velocity extremes, max/min)
At equilibrium, ½ mvmax2 = ½ kA2
Center of Mass
sum of (mass * position) / total mass
For any system of masses, there is one point that moves as if the entire mass of the system were concentrated in it/all the forces were applied to it (ie one point that is representative of the multi-particle system)
located at a point called the “weighted average of masses” → in highly symmetrical (uniform) cases, it’s the geometric center of the object
FOR AN IRREGULAR OBJECT, integrate instead of taking the sum of
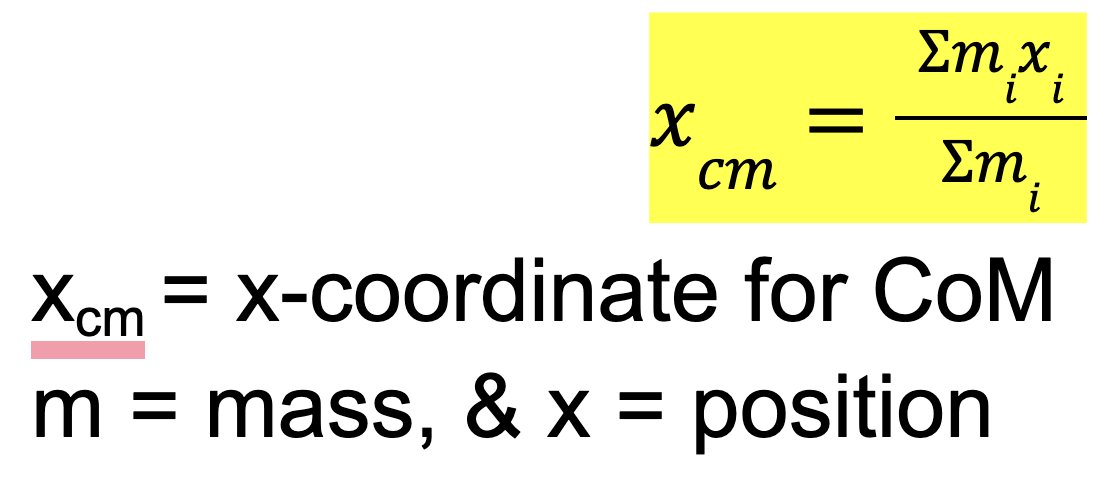
Center of Gravity
the point at which the net force of gravity acting on the system can be assumed to be applied
Generally, the center of gravity (CoG) is not the same as the center of mass (CoM); BUT for almost any existing object, the two points pretty much coincide (very very close) so it's ok to say they are the same
The CoG and the CoM coincide for any system of masses located in a uniform gravitational field → in practical terms, it means that the system/object is much smaller in size than the planet nearest to it (so like, any object on Earth)
Velocity of the center of mass
can be found by taking the derivative of the center of mass
vcm ∑mi = ∑mivi
The velocity of the center of mass can help you find the total momentum of the system
Momentum (ρ)
mass (m) times its velocity (v)
ρ = mv
IT IS ONE OF ONLY 3 QUANTITIES THAT ARE CONSERVED IN AN ISOLATED SYSTEM (the other two being energy and angular momentum)
F = dp/dt —> change in momentum over change in time
Impulse (J)
Impulse is the change of momentum of a particle
J = ∆p = F∆t
Impulse can also be the area under a Force-time graph (the integral, F∆t… duh)
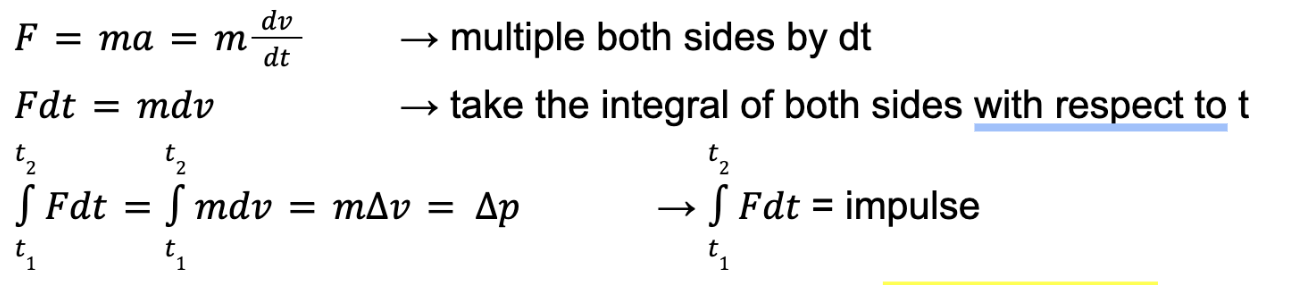
A ball of mass 𝑚 is dropped from rest at a height ℎ and collides elastically with the floor, rebounding to its original height. What is the magnitude of the net impulse on the ball during the collision with the floor?
net impulse is the change in momentum of the ball during its collision with the floor
set KE equal to PE to find initial speed → ½ mv2 = mgh → v = √2gh
The ball returns to the same height when it leaves the floor; thus, the final speed for the ball during the collision with the floor is the same as the speed when the ball reaches the floor, but it will be moving in the opposite direction (so opposite sign) → ∆p = pi - pf = m(vi - vf) = m(√2gh - (-√2gh)) = m√8gh
TAKE-AWAY: if it rebounds to the same position/same height, the object has the same speed after the collision as before
A space shuttle has a mass of 90,000 kg. In order to stay in a circular orbit, it must have a velocity of 8000m/s. The pilot discovers that the shuttle has slowed down to 7900m/s and the shuttle’s speed needs to increase. If the thrusters exert a constant force of 50,000N, how long do the thrusters have to exert this force in order to return the shuttle to orbital velocity?
J = ∆p
Ft = m(vf - vi)
t = m(vf - vi)/F = (90,000)(8000-7900)/50,000
t = 180s
Types of Collisions
Linear momentum is conserved in ALL collisions
In inelastic collisions and explosions KE is NOT conserved
KE IS conserved in elastic collisons
In elastic collision, the objects do not stick together
Ballistic Pendulums
used to analyze the initial velocities of launching systems
Has 3 components: the launch, the collision, and the swing. In the launch and swing, energy is conserved. However, energy is not conserved in the collision (only linear momentum). —> analyze each part seperately
2D Collisions
Objects collide and go in different directions; use vectors to solve these types of problems
can use the Pythagorean theorem: p02 = pA2 + pB2
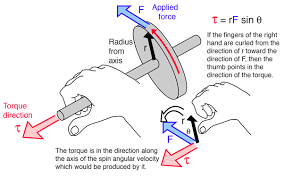
Torque
torque = distance * sinθ * Force
When r & F are maximum, and θ = 90o → torque maximum
0 < θ < 90 → intermediate torque
Rotation depends on the force applied (direction & magnitude), the distance between force applied & pivot point (i.e. moment arm), & the angle at which the force is applied → together this is torque
Pivot Point (AKA fulcrum, hinge): the point at which the object rotates about
Moment Arm: the perpendicular distance from the pivot point to where the force is being applied
Right Hand Rule for Torque
wrist = pivot point
fingers point in the direction of r (distance)
fingers CURL in the direction of F
thumb points in the direction of torque
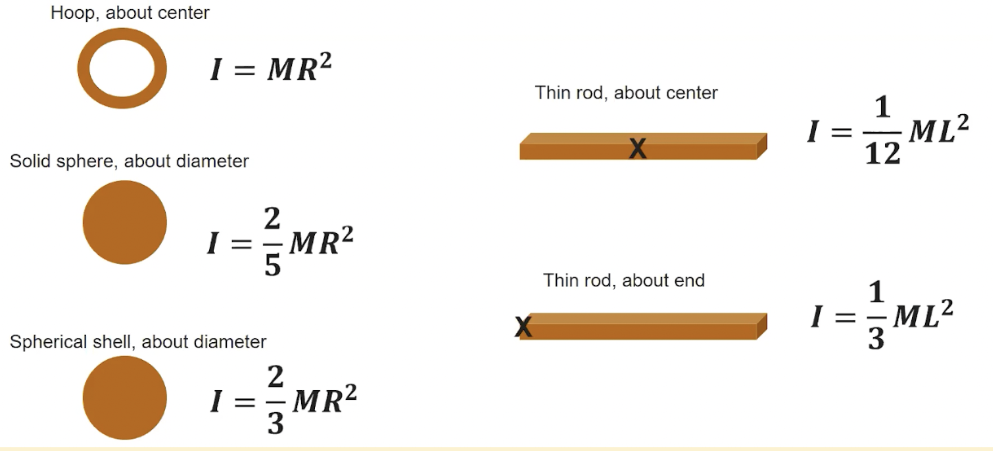
Rotational Inertia (I)
Inertia is a resistance to change (qualitative)
Mass is the quantitative value of inertia, measured in kilograms (kg)
Rotational Interia (I) is a resistance to change in rotational motion; it depends on both mass and location (of the mass)
Rotational Inertia of point particles: I = ∑mr2
r = distance of mass from pivot point
if I want my rotational inertia to be as large as possible, the pivot point should be as far as possible from the largest mass
the sum of becomes an integral symbol for a non-rigid body
The rotational inertia is greater when the mass of an object is further away from the center (ex. out of a hoop and sphere with the same mass and radius, hoop has more rotational inertia )
Parallel Axis Theorem
To find the rotational inertia of an object rotating about a point that is NOT its center of mass
I = Md2 + Icm
Icm = rotational inertia about the center of mass
M = mass of the object
d = distance from center of mass to pivot point
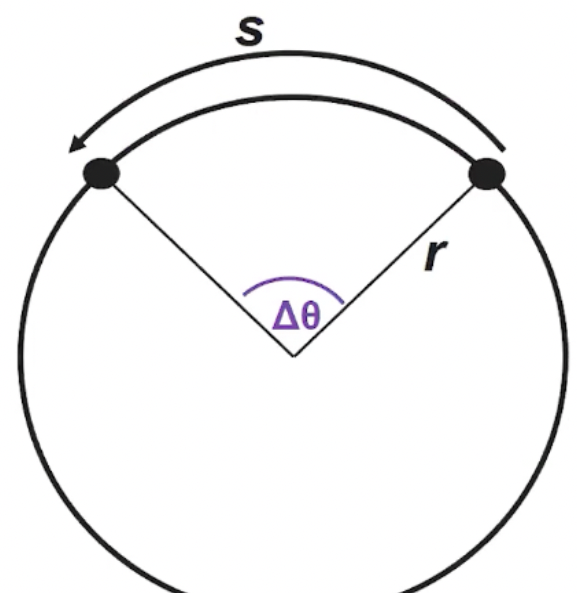
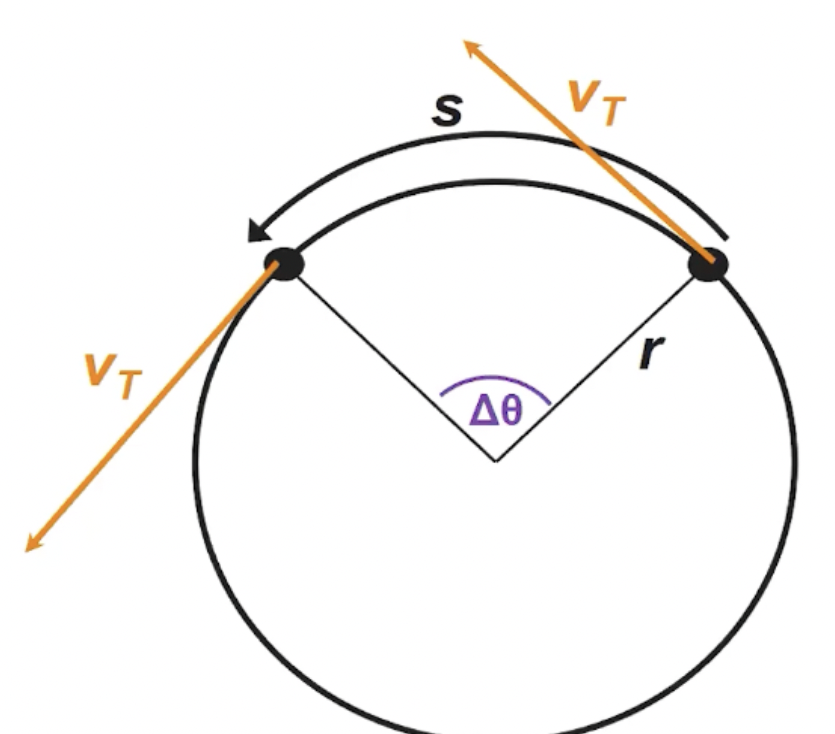
Angular displacement (∆θ)
A particle that rotates through an angular displacement also translates through a distance s (arc length)
s = r(∆θ) → on the equation sheet (backside w/ all the geom)
Angular velocity (ω)
how long it takes an object to rotate through an angle → ω = dθ/dt (rad/s)
The tangential velocity (linear) is tangent to the circular motion
RIGHT-HAND RULE FOR ω: fingers curl in the direction of rotation and thumb points in the direction of ω (this direction is along the axis of rotation)
*note: as the radius of rotation changes, the arc length changes. A smaller radius means a shorter arc length. This affects the tangential velocity (smaller radius = slower tangential velocity) → as long as the radius of the rotation remains the same, the angular velocity won’t change though.
Uniform rotation → v = rω
Angular acceleration (α)
α = dω/dt = d2θ/dt2
The direction of both tangential and angular acceleration is parallel (when the object is speeding up) or antiparallel (when the object is slowing down) to the tangential/angular velocity (respectively)
Equations for Uniform Rotational Motion
ω = ω0 + αt
θ = ω0t + ½ αt2
ωf2 = ω02 + 2αθ
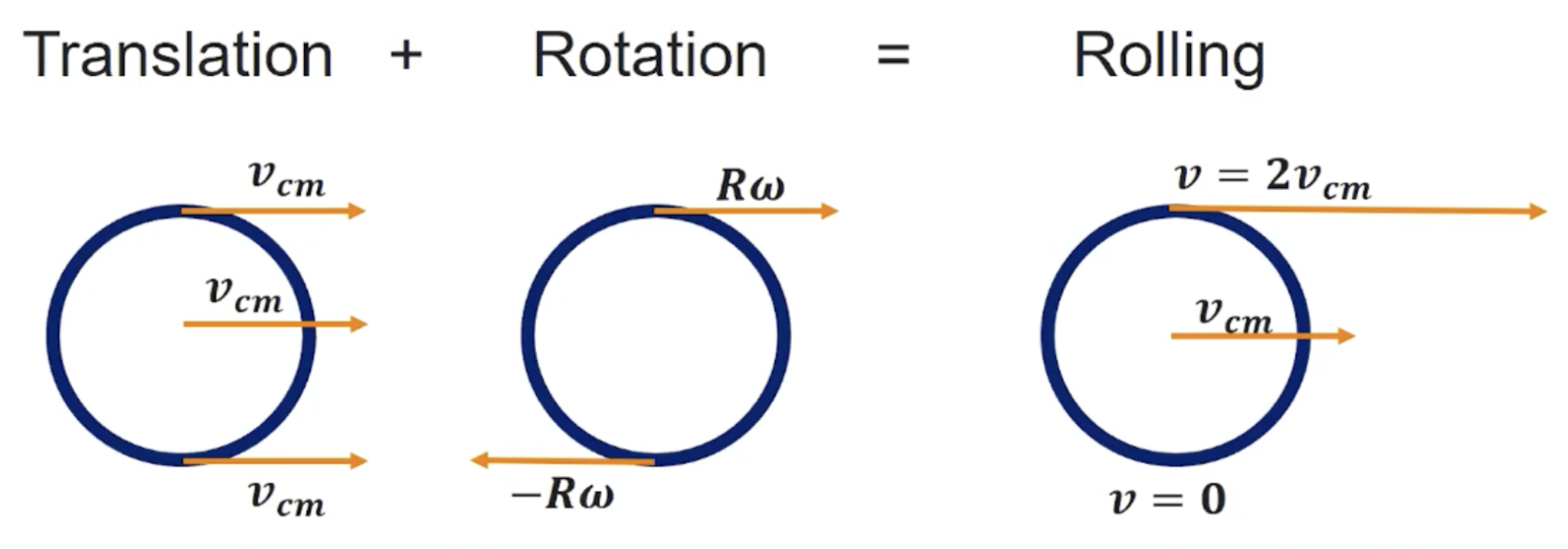
Rolling w/out Slippling
CONDITION: center of mass —> v = ωr
it has both translational and linear properties
Friction does not do work on an object rolling w/out slipping because there’s no displacement of the point of application of a force
Static friction makes rolling w/out slipping possible; the point where the bottom of a wheel touches the surface is instantaneously at rest, but the rest of the wheel rotates about a rotation axis through a point
We call it “rolling w/out slipping” because the rolling is uniform and the velocity (tangential) is constant
Newton’s Second Law for Rotation
If the sum of torques on an object is non-zero, the object will experience angular acceleration
α = (∑τ)/I
Angular Momentum (L)
L = r(mv) * sinθ = r * p * sinθ —> particle
L = Iω —> extended rigid body
Conservation of angular momentum
τ = dL/dt —> if τ = 0, then ∆L = 0, so the final and initial angular momentum is the same
angular momentum is conserved when there is no torque
remember: if the force acts at the point of rotation, then the torque is 0 (because the distance from the point where F is applied is 0)
position/velocity/acceleration
instantaneous velocity: dx/dt → velocity at a specific point
average velocity: ∆x/∆t
instantaneous acceleration: dv/dt
the area under a velocity-time graph is the displacement
Note: you can use these relationships for non-uniformly accelerated motion problems. Use kinematic equations (on eq sheet) for UAM problems
Free Fall Problems
an object is in free fall if gravity is the only force acting on it
the acceleration of an object in free-fall is g = 9.8 m/s2 throughout the motion
at the peak of any trajectory, y-component of velocity is ZERO
(because the graph is a parabola, and conservation of energy) an object’s speed as it passes a certain height is the exact same on the way up and on the way down; the magnitude of the time difference to the peak of the trajectory is also the same
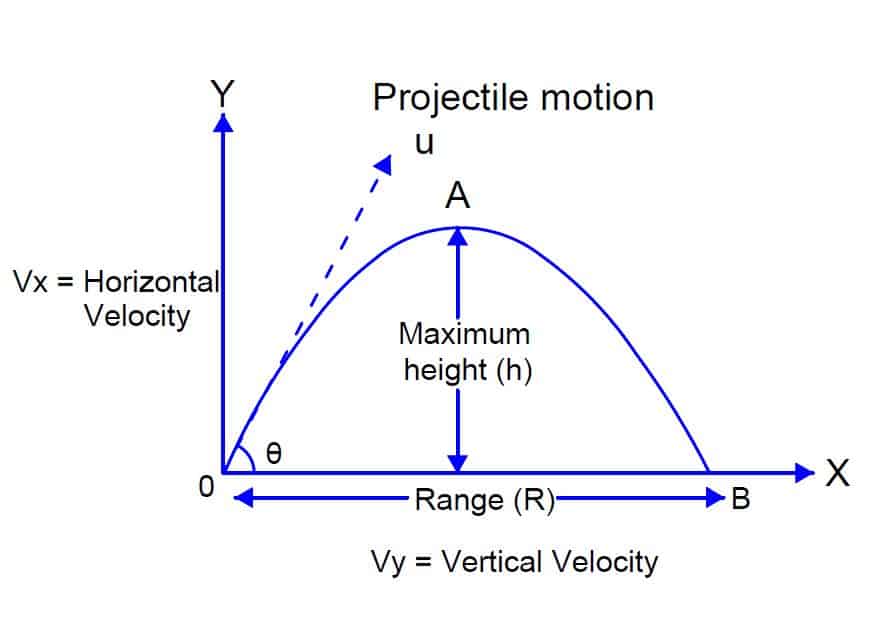
Projectile motion
the object only experiences the force of gravity (in the y-direction) → ay = g
there is NO net force in the x-direction → no acceleration in the x-direction → vx is constant, ax = 0
time connects the two directions; the UAM equations can be used here
Range = (v2 sin2θ)/g
Rangemax = gt2/4
h(t) = - ½ gt2 + vyt + h0 → h0 = initial height
vx = vcosθ, vy = vsinθ
t = 2vsinθ
hmax = v2sinθ/2g
Uniform Circular Motion
when an object moves at a constant speed in uniform circular motion, its acceleration is NOT zero
the direction of the velocity is tangent to the circle in the direction of the motion
v = rω
the direction of the acceleration vector is always toward the center of the circle
the magnitude of the acceleration is given by a(t) = v2/r → centripetal accel.
tangential acceleration (parallel to velocity) only affects the magnitude of the velocity vector. radial acceleration (perpendicular to velocity) affects the direction
when tangential accel. is non-zero and radial accel. is zero, only direction changes → if tangential accel. is constant, then it is uniform circular motion
when tangential accel. is zero and radial accel. is non-zero, the direction never changes; the object moves in a line with changing speed
Fnet = mv2/r → UCM, Fnet must be pointed to the center of the circle
Newton’s First Law → Inertia
Inertia is how much an object resists a change in velocity and is measured by mass → the idea that it is harder to change the motion of a more massive object
If an object is at rest (static equilibrium), or in motion with CONSTANT velocity (dynamic equilibrium), then it must have zero acceleration and zero net force
Fnet = 0 ←→ a = 0
Newton’s Second + Third Laws
Fnet = ma
For every force exerted by one object on another, there is another force equal and opposite to it → applies only to a pair of objects, not a singular object alone
Mass v. Weight
mass is a measure of inertia (SI Unit = kg) → an object has the same mass anywhere in the universe
weight is the magnitude of the force exerted on an object by the closes planet; it is not the same everywhere in the universe → weight = mg
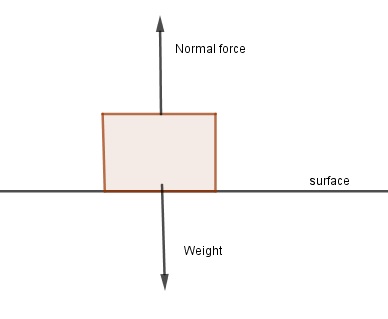
Normal Force (FN)
magnitude is determined by F = ma
it is always PERPENDICULAR to the surface is on and pointing away from it (the surface)
Frictional Force (Fs)
the magnitude can be determined from experiments
Fs is parallel to the plane of contact between two objects, and it is opposite in direction to the motion
An object has static friction when it is at rest. As long as the applied force is less than the threshold, the object won’t move and Fs is equal to Fnet → Fstatic friction ≤ µsFN
An object has kinetic friction when it is moving, Fkinetic friction is always lower than the maximum Fstatic friction → Fkinetic friction ≤ µkFN
Work
dW = Fnet * dr
W = F∆r → work due to a constant net force
Area under a Force-position graph is work
W = mvf2/2 - mvi2/2
Work-Energy Theorem
Kinetic Energy = the energy of an object in motion → KE = ½ mv2
Wnet = ∆KE
W = -∆U
Conservation of Energy
Energy is conserved → total energy of a system is equal to the sum of its kinetic and potential energy at any point
Etot = KE + U
U = mgh
Ug → gravitational PE → W = mg * ∆r
The energy dissipated means energy lost → if an object in motion is coming to rest on a flat surface (the PE doesn’t change cuz its height doesn’t), the initial KE is the final energy dissipated.
Spring Force (Hooke’s Law) & Elastic PE
Force due to a spring: Fx = -kx
k → spring constant
x → displacement from equilibrium position
Uelastic = ½ kx2
Power (P)
P = W/∆t → Units: J/s
Fx = -dU/dx → valid only when there are no non-conservative forces
When force is constant, P = Fv
Two blocks rest on a table. The bottom block is pulled to the right by an applied force 𝐹 that is strong enough so that the two blocks do not move together (i.e., they do not have the same acceleration or velocity). There is friction between the blocks, but the tabletop is frictionless. When the top block leaves the bottom block, where does it land and why?
The top block will land to the right of where it starts because of the kinetic friction between the blocks.
![<ul><li><p><span style="color: blue">position: x(t) = </span><strong><span style="color: blue">A*sin(ωt)</span></strong></p></li><li><p><span style="color: green">velocity: v(t) = d/dt [x(t)] = </span><strong><span style="color: green">Aω * cos(ωt)</span></strong></p></li><li><p><span style="color: red">acceleration: a(t) = d2/dt2 [x(t)] = d/dt [v(t)] = </span><strong><span style="color: red">-Aω2 * sin(ωt)</span></strong></p></li></ul>](https://knowt-user-attachments.s3.amazonaws.com/de680bf3-cec9-4ef8-af90-ab0eb336ced1.png)
Note
Flashcard