Foundations of Statistical Inference and inferential statistics

research pt. 6 (time will be heavy on the exam)

foundations of statistical inference

allows for predictions and conclusions to be made

inferential statistics basics

probability, empirical rule, and confidence interval

probability

likelihood that any one event would occur (p)

• measured as a decimal version of the percent chance (so 16.6% would be p = 0.167)

• if the event must occur, p = 1.00

• if the event will not occur, p = 0.00

• p < 0.05 is signficant

empirical rule

the 68-95-99.7 rule

• the pattern of percent of data which lies 1, 2, and 3 SDs from mean. You can then use this to determine the probability of an event in a normal distribution

Confidence Interval

range of values used to eliminate unknown pop parameter (like a mean) based on sample data, giving you an idea of the precision of your estimate and how confident you can be of your estimate. should be presented as a percentage

• wider boundaries = inc confidence, dec precision

• interpretation ex: 95% CI, with CI = 6.8 ± 0.4116. We would say “ we can be 95% confident that the population mean will fall between 6.39-7.21”

• we do not want the CI to cross 0

• P value + CI will always result in a sum of 100%

Sampling error

error is inevitable. this particular error means that the sample reflects the difference between results obtained from your sample and the truth about the population. As sample size increases, sample sets become more representative of the population. So a larger n value means less sampling error!

Point estimate

single value obtained by direct calculation, using sample mean to estimate population mean. likely contains some degree of error

interval estimate

specifies a range within which the population parameter should lie. This is the more meaningful method

hypothesis testing

draws conclusions about population, based on sample data

null hypothesis (Ho)

differences occurred due to chance, rather than intervention (means of control and case groups are the same)

alternative hypothesis (research hypothesis)

group means are different

• non-directional simply says they are not the same

• directional says one is greater than the other

• Ex: for pts with limited shoulder mobility, mean change in Sh ER will be greater/lesser for those who receive mobilization than for those who do not receive mobilization. Errors can occur in hypothesis testing, too: Type I and Type II

Type I

rejecting null when it is true (stating difference, but really none)

• level of significance (a) - probability of Type I error.

• if p = /< .05, reject the null - this means there’s a 5% change of Type I error

Type II

not rejecting null when it is false (stating no difference, but really there is)

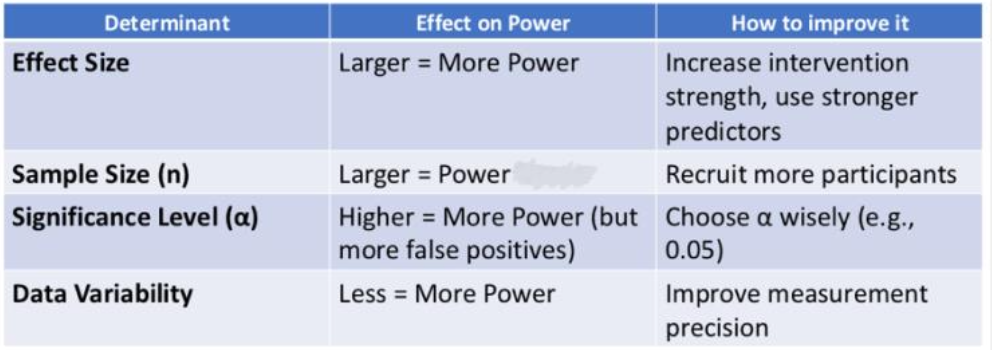
• power (1-beta) measures how good the test is at detecting a real effect when one actually exists - of actually rejecting a false null. Beta is the probability of making Type II error. Our goal is to have a high power (80%), beta = 0.20

• without enough power, we risk concluding that an intervention doesn’t work when it actually does! And if that happens, we risk abandoning a good intervention idea

• power analysis

power analysis

good for determining sample size and probability of Type II error

a priori

before the study. used to determine n

post Hoc

after the study. used to determine power and may assist in explaining any potential significance results

effect size (d or standardized mean difference, SMD)

measures how big or important a different is between groups/variables. it is possible to have a p that is insignificant, and a large effect size - we focus more on p, so in this instance, the other stuff doesn’t matter!

• cohen’s d: small = .2, medium = .5, and large >.8

• pearson’s r: small = .1-.3, medium = .3-.5, large = >.5

*Also has a connective to SD! We want our two samples to be separated in regard to SD

chart of determinants

inferential statistics

parametric statistical tests and t-tests for parametric

parametric statistical tests

requires three assumptions:

• normal distribution

• variance

• interval or ratio scales

*these tests are generally more powerful and can test a wider range of alternative hypotheses

normal distribution

samples are randomly drawn from a population with a normal distribution

normality

shapiro-wilk or kolmogorov-smirnov (p >0.05, because the null hypothesis is that there is a normal distribution

variance

samples being compared are roughly equal

• Levene’s (p > 0.05). This is the rare time when we WANT a non-significant (>) result - it means groups are homogenous!

interval or ratio scales

data should be measured on the interval or ratio scales (continuous data)

• for a parametric test, we usually want n = or > 30, so just be aware of that with the textbook’d sample questions. but regardless of number, the exam will be clear whether or not yu need to use parametric!

t-tests for parametric

significance of difference between two group means is judged by a ratio. t = diff between groups/variability within groups. Basically numerator = mean of different scores and denominator = standard error the difference scores. T will be large if the difference is significant

• independent (unpaired) and Paired (correlated, matched)

independent t-test (unpaired)

• two independent groups (whether case and control, or two cases getting different txs)

• homogenous groups

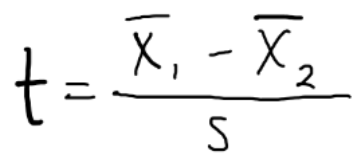
paired t-test (correlated, matched)

• tend to be more powerful

• repeated measures, or where participants are exposed to both conditions (they are their own controls). Analyzes a difference score and reduces error variance

*be careful - multiple t-tests increase chance of error (if you need to compare three or more ANOVA)

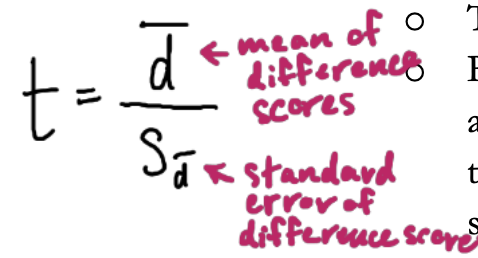
research deign or inferential statistic

how to determine which parametric or nonparametric inferential statistic to use?

what is the research design?

1. list the independent variable (s)

2. for each IV, is it a between or within IV

3. list the dependent variable (s)

4. list the level or measurement scale for each DV

5. the research design used is _____

What inferential statistic should be used?

1. is the data parametric or nonparametric?

2. how many means are being compared?

3. are the means paired or unpaired?

4. the statistic that should be used is _____