acts 430

damages of non constant variance

biased estimates, make the OLS estimates LESS EFFICIENT because equal weights has been assigned regardless of the info contained in each observation

assumption of constant variance can be checked by examining

scale-location plot

how do we deal with non constant variance

transform observations (non constant variance transformation); use another estimating method: weighted lease squares; model the variance (arch/garch)

model diagnostics

E(Ei)=0

Var(Ei) constant

Cov(Ei,Ej)=0, i=/j

Ei~N(0,var)

check outliers and high leverage points

the variance of standardized residuals is approximately ____, but only approximately because…

1, their definition DOESNT take account the correct variance

violation of E(Ei)=0 caused by…

inappropriate model structure (effect of explanatory variables may enter model in a different way)

negligence of some important explanatory variables (STEPAIC)

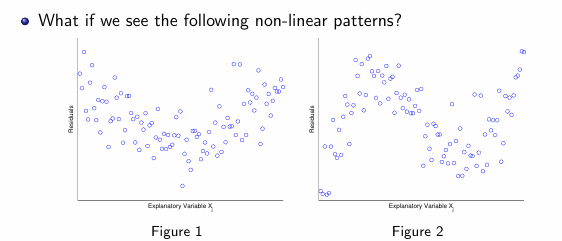
if a model is adequate, what should we expect to see when we plot residuals against Xj?

random scatter plot

an added variable plot is useful when

deciding whether a new explanatory variable should be included

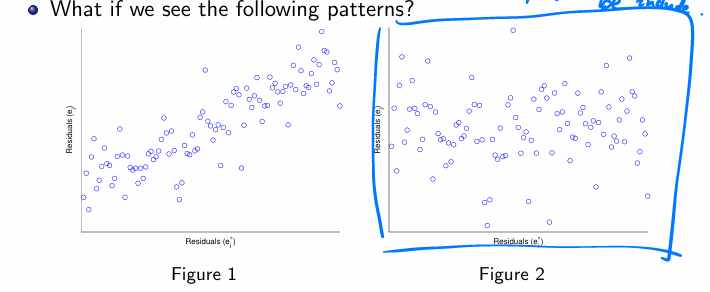
residual plots for checking E(Ei)=0:

checking residuals from X* and original residuals.

Figure 1: theres a pattern, so addition of X* may improve model

Figure 2: random scatter plot, may not need to include X*

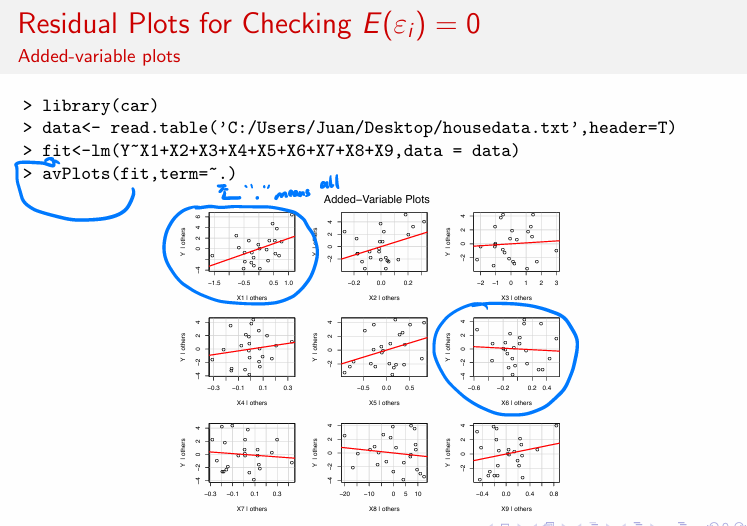
Plot with a clear slope / pattern (your left blue circle)

• Points follow an upward or downward trend

• Red line is noticeably sloped

• Interpretation:

  • Xk has a nonzero partial effect

  • Xk likely belongs in the model

  • Omitting it could violate E(εi)=0

partial residuals plot shows the relationship

b/w a given explanatory variable (Xj) and the response (Y) given that other independent variables are also in the model

BACKWARD LOOKING

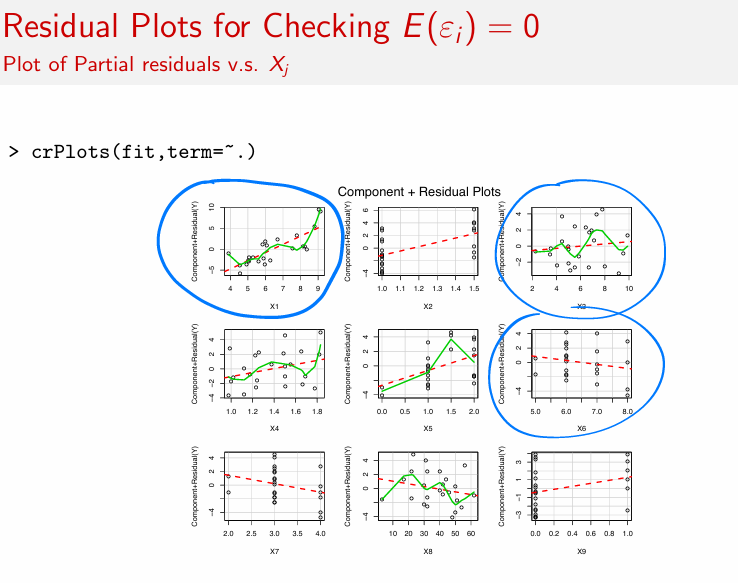
Circled plots with curvature (top left, top right)

• The green smooth curve bends away from the red dashed line

• This suggests:

  • The relationship between Y and Xj is not linear

  • Even if Xj is important, the model is misspecified

• Typical fix:

  • Add Xj^2​, log(Xj), or a spline term

👉 These variables belong, but not in a simple linear form.

heteroscedasticity

variability of a collection of random variables is unequal

when consider log transformation

when standard deviation of y is proportional to the mean. regress ln(yi) on the explanatory variables

QQ plot compares…

quantile of data sample and quantile of the theoretical distribution

QQ plot: if the residuals don’t come from a normal distribution.

steeper —>

flatter —>

steeper —> fat tailed

flatter —> light tailed

outlier is an observation that has an extreme _____ value. treat a point as an outlier if the …

high leverage point is an observation that has an extreme ____ value. leverage can be assessed through …

influential point is an observation …

we use what to measure the influence of an outlier or a high leverage point

outlier is an observation that has an extreme response value. treat a point as an outlier if the standardized residual exceeds 2 in AV

high leverage point is an observation that has an extreme explanatory variable value. leverage can be assessed through …

influential point is an observation where including/excluding point can have a big impact on regression result

cooks distance

cooks distance

sum of all the changes in a regression when a data point is removed

when interpreting results from multiple regression, the main goal is

convey the importance of the individual variables, or effects, on an outcome of interest

readers of a regression study first want to understand the

direction (sign) and magnitude (size) of individual effects

consequences of overfitting the model

increase resulting sigma hat squared due to a smaller value of denominator (n-p-1)

including extraneous variables would NOT lead to bias. but the standard error would be larger than if we had correct model (less efficient)

consequences of underfitting

bias estimates

increase sigma hat squared due to biased estimates

larger sigma hat squared inflates PI and produces inaccurate test results regarding importance of explanatory variables

more serious than overfitting

potential pitfalls when collecting data

sampling frame error and adverse selection

limited dependent variables, censoring, truncation

if sample not representative, taking a larger sample

DOES NOT remove bias

drawbacks of using old modeling technique

poor fitted values - yi only takes the values of 0 or 1 but yhati can be continuous

heteroscedasticity - var(yi) varies depending on different obs

meaningless residual analysis

logit and probit functions are both _____. they are similar in that they are almost linearly related over the interval .1<p<.9, so the function choice is dependent on…

nonlinear functions

preference

for simple linear relationship, y=B0+B1+E,

if E=0, the 95% confidence interval is equal to the 95% prediction interval

The prediction interval includes the irreducible error, but in this case it is zero.

for simple linear relationship, y=B0+B1+E,

the prediction interval is always at least as wide as the confidence interval

Because it includes the irreducible error, the prediction interval is at least as wide as the confidence interval.

confidence interval quantifies what range?

E(y/x)

forward step selection

greedy

starts w intercept and then adds explanatory variable that most decreases SSres at each stage. rather than explore all possible models, looks for a good yet easy to compute path thru them

backward step selection

start w full model and delete explanatory variable that is least significant. ends when all explanatory variables are statistically significant

AIC

nested models

BIC

non nested models

visuals for whether we should alter model structure?

residuals vs Yhat

residuals vs Xj, j=1.,,,p

visuals for whether we should add a particular explanatory variable?

added variable plots (partial regression plot)

partial residuals plot

ridge regression:

modifies…

L_ regularization

tuning parameter controls… and is determined by …

modify SSres by including an additional shrinkage penalty term

L2 regularization because second order magnitude is imposed as the penalty

tuning parameter, lamda, controls the relative impact of the penalty and is determined separated via CV

ridge regression improves OLS in terms of

MLE

disadvantage of ridge regression

it would always include all explanatory variables in the final model

lasso regression

stands for?

L_ regularization

least absolute shrinkage and selection operator

L1 regularization because the first order magnitude is imposed as the shrinkage penalty

compared to ridge regression, lasso regression has the ability to force some of the B’s to be exactly = 0 when lambda is sufficiently large