Geometry: Unit 10 Circles- Tangents, Chords, Arcs, Angles
Geometry: Unit 10- Circles 6.0-6.3
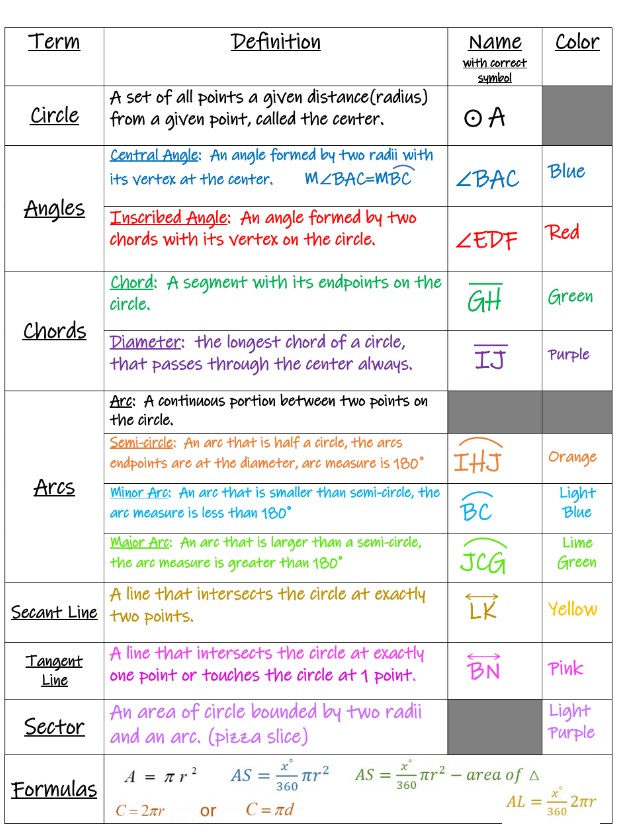
<<6.0 Circle Terms & Properties<<
<<6.1 Tangent Properties<<
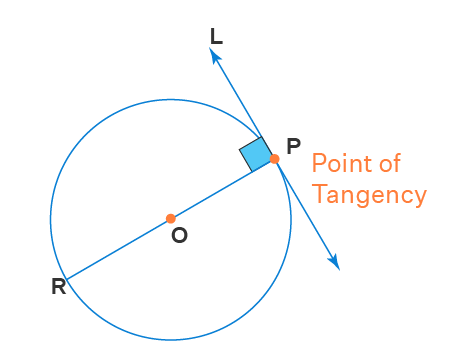
Tangent Conjecture:
A tangent to a circle is perpendicular to the radius drawn to the point of tangency.
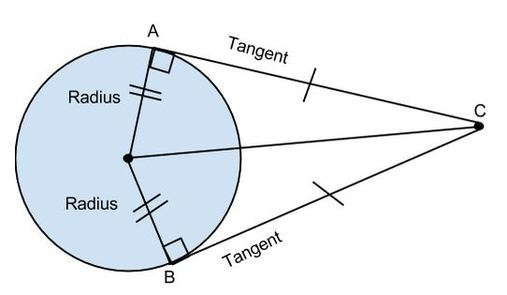
Tangent Segments Conjecture:
Tangent segments to a circle from a point outside the circle are congruent.
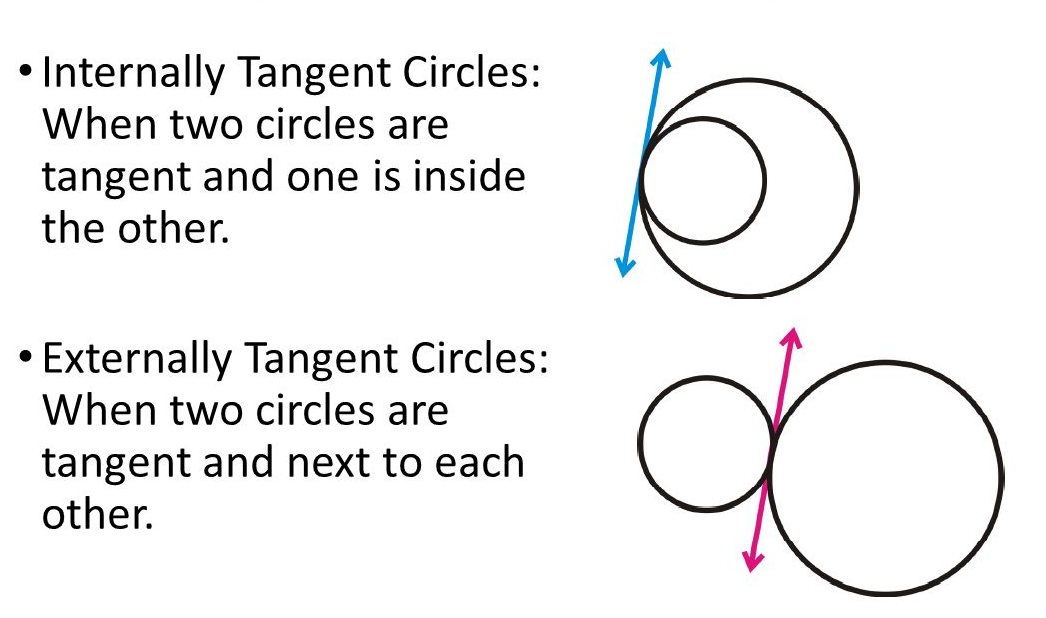
Tangent Circles:
Two circles that are tangent to the same line at the same point. They may be externally tangent or internally tangent.
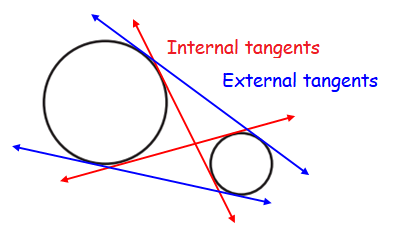
Common Tangent: A line tangent to two or more circles. They may be externally tangent or internally tangent. When two circles do not share the same point of tangency but still share a tangent line.
<<6.2 Chord Properties & Arcs<<
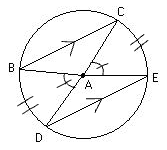
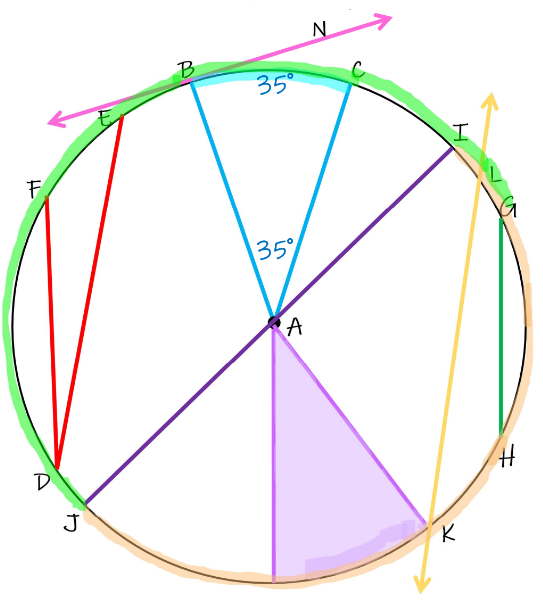
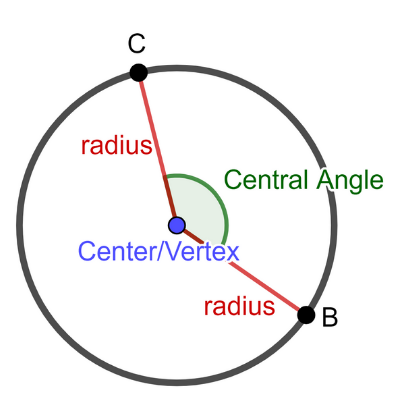
Central Angle:
An angle made up of two radius on the circle’s circumference with its vertex at the circle’s center. The measure of the central angle is equal to the measure of its arc.
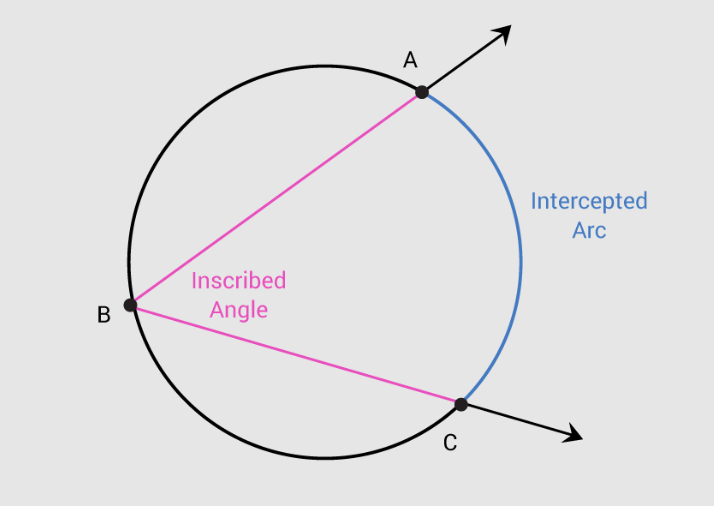
Inscribed Angle:
An angle made up of two chords with its vertex on the circle’s circumference.
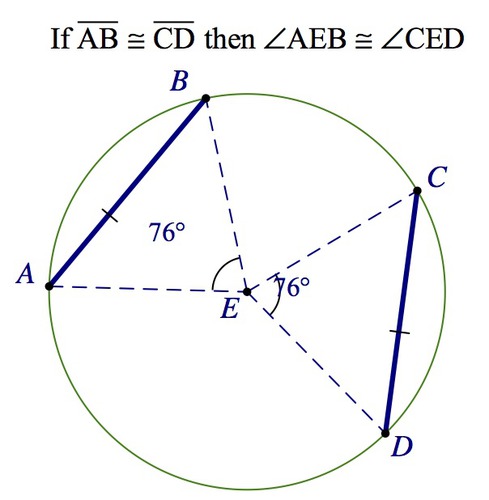
Chord Central Angles Conjecture:
If two chords in a circle are congruent, then they determine two central angles that are congruent.
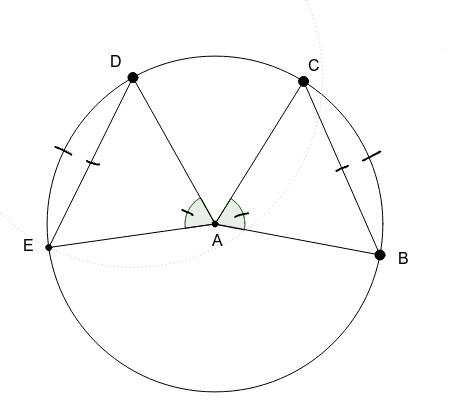
Chord Arcs Conjecture:
If two chords in a circle are congruent, then their intercepted angles are congruent.
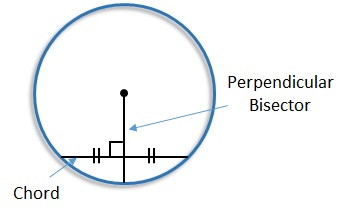
Perpendicular to a Chord Conjecture:
The perpendicular from the center of a circle to a chord is the bisector of the chord.
Chord Distance to Center Conjecture:
Two congruent chords in a circle are equidistant from the center of the circle.
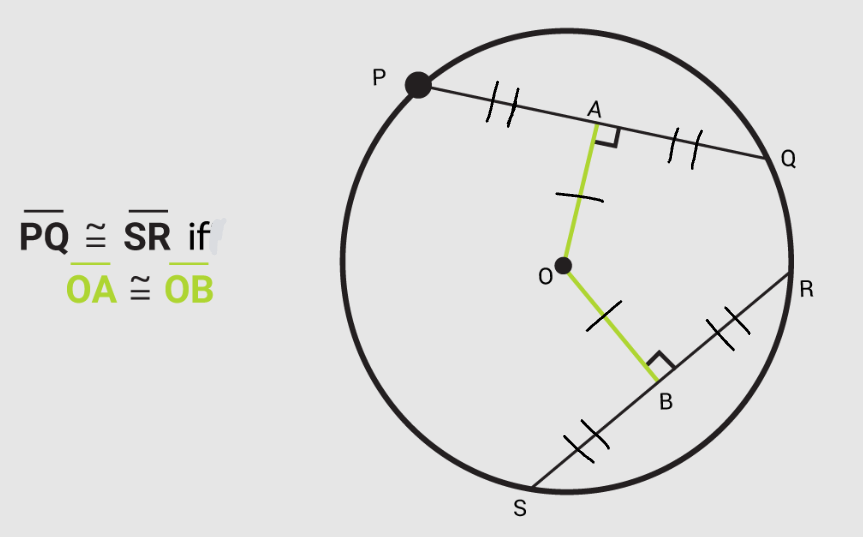
Perpendicular Bisector of a Chord Conjecture:
The perpendicular bisector of a chord passes through the center of a circle.
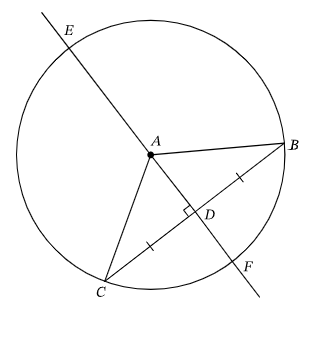
<<6.3 Arcs & Angles<<
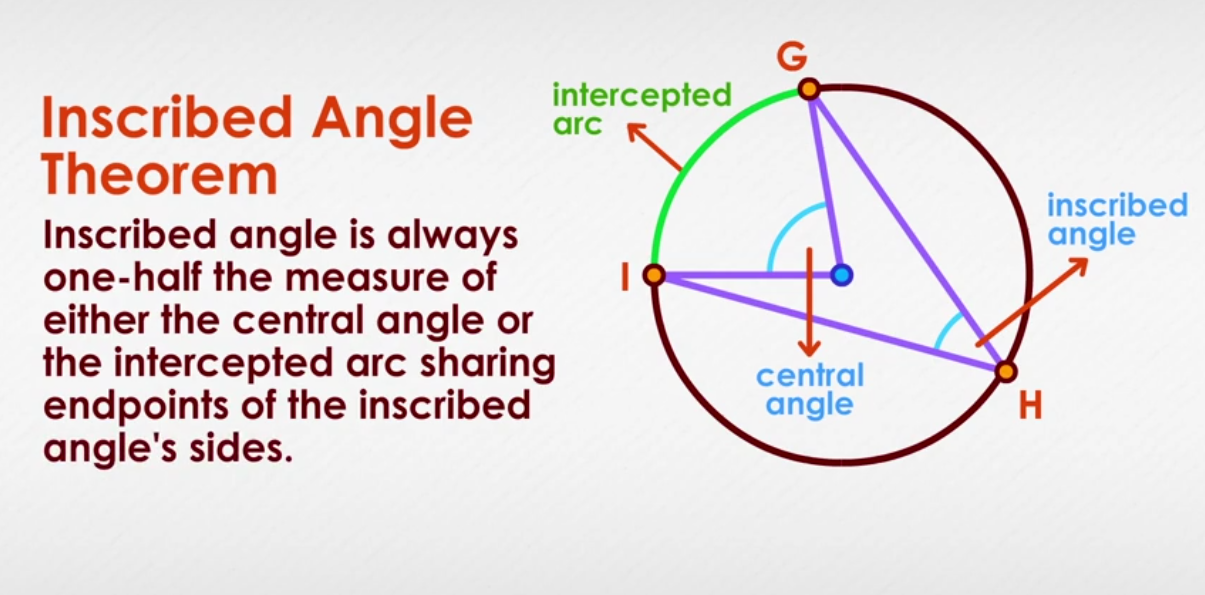
Inscribed Angle Theorem:
The measure an inscribed angle is half the measure of its intercepted arc.
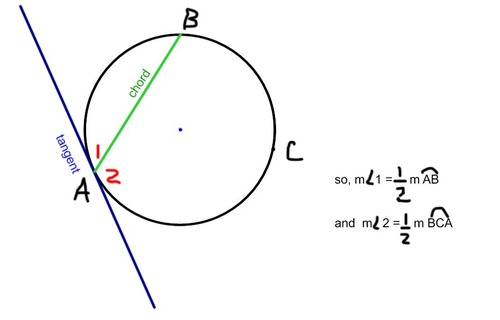
Angle Formed by a Chord and a Tangent Conjecture:
The measure of an angle formed by a chord and a tangent is half the measure of its intercepted arc.
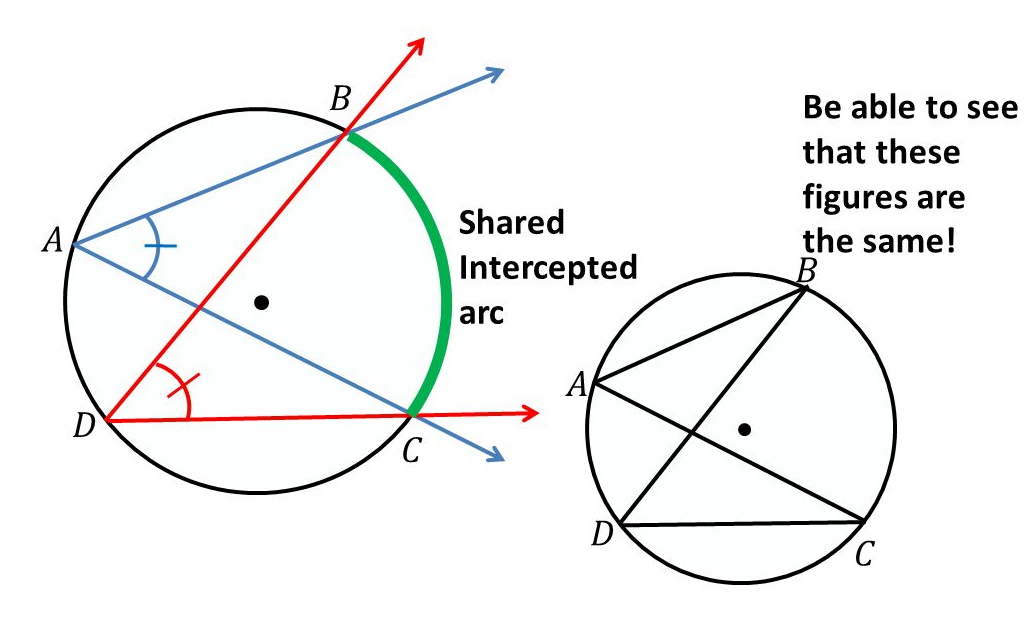
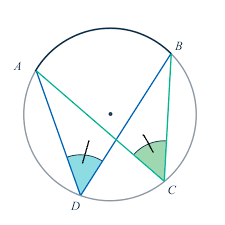
Inscribed Angles Intercepting Arcs Conjecture:
Inscribed angles that intercept the same arc are congruent.
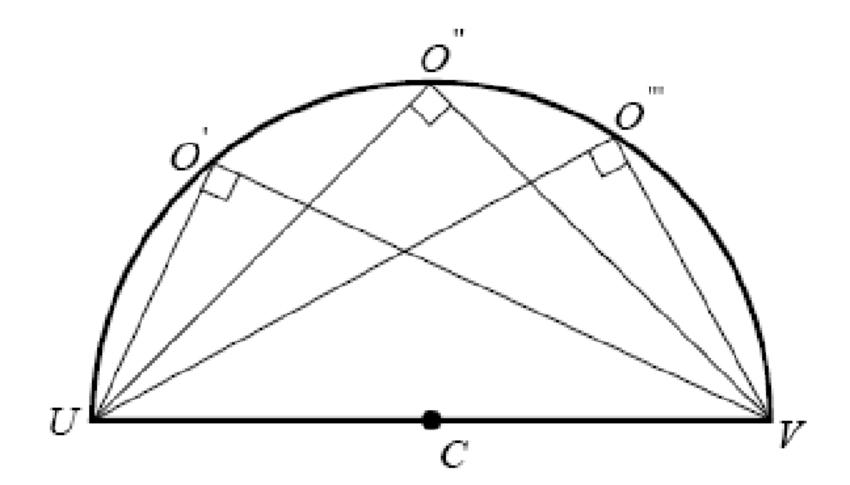
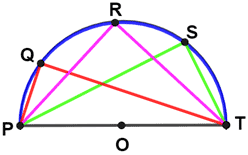
Angles Inscribed in a Semicircle Conjecture:
Angles inscribed in a semicircle are right angles.
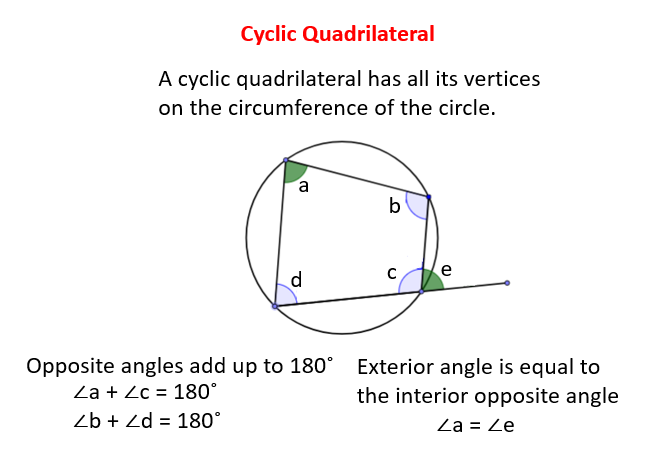
Cyclic Quadrilaterals:
A quadrilateral inscribed in a circle is called a Cyclic Quadrilateral. The two opposite angles in a cyclic quadrilateral add up to 180 degrees.
Arcs by Parallel Lines Conjecture:
Parallel lines intercept congruent arcs on a circle.