MEC320 - Full Set - (Papers + Tutorial Sheets)

A combination of the tutorial sheets and past papers for MEC320

What is the physical meaning of the convective derivative?

(a) The time rate of change following a moving fluid element.

(b) The time rate of change at a fixed point.

(c) The time rate of change due to the movement of the fluid element from one location to another in the flow field where the flow properties are spatially different.

(d) None of the above.

c) The time rate of change due to the movement of the fluid element from one location to another in the flow field where the flow properties are spatially different.

Select the correct answer that mathematically describes a 3D, steady-state compressible flow.

a) \frac{\partial (\rho u)}{\partial x} + \frac{\partial (\rho v)}{\partial y} + \frac{\partial (\rho w)}{\partial z} = 0

b)\frac{\partial(\rho}{\partial(t)}+\left\lbrack\frac{\partial(\rho u)}{\partial x}+\frac{\partial(\rho v)}{\partial y}\right\rbrack=0

c)\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0

d)\frac{\partial\rho}{\partial t}+\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0

a) \frac{\partial (\rho u)}{\partial x} + \frac{\partial (\rho v)}{\partial y} + \frac{\partial (\rho w)}{\partial z} = 0

In a fully developed flow within a straight channel with its axis along the x direction, which of the following term is negligible?

(a) du/dx

(b) du/dy

(c) Both du/dx and du/dy

(d) None of the terms are negligible.

a) du/dx

.Consider the flow of an incompressible fluid between two infinite horizontal parallel plates placed at y=0 and y=H. The plates are fixed and the flow is driven by a constant pressure gradient in the streamwise direction -dp/dx = G > 0. The laminar velocity profile inside the channel is given by u(y) = (G/2μ)y(H-y). What is the correct expression for the wall shear stress (τw) on the plane y=0?

a)\tau_{w}=\mu\frac{GH}{2}

b)\tau_{w}=\frac{GH}{2}

c)\tau_{w}=\frac{GH}{2\mu}

d)\tau_{w}=0

b)\tau_{w}=\frac{GH}{2}

What is u+?

a) The ratio of velocity parallel to the wall to the friction velocity

b) The ratio of the friction velocity to velocity parallel to the wall.

c) The ratio of free-stream velocity to friction velocity.

d) The ratio of friction velocity to free-stream velocity

a) The ratio of velocity parallel to the wall to the friction velocity.

The terms in the momentum equations accounting for turbulence effects contain ____________.

a) Reynolds stresses

b) Turbulent kinetic energy

c) Dissipation of turbulent kinetic energy

d) Length scale terms

a) Reynolds stresses

Which of these scientists introduced turbulent viscosity?

a) Kolmogorov

b) Smagorinsky

c) Prandtl

d) Boussinesq.

d) Boussinesq

The kinematic turbulent viscosity is __________.

a) equal to the product of turbulent length and time scales

b) equal to the product of turbulent length and velocity scales

c) proportional to the product of turbulent length and velocity scales

d) proportional to the product of turbulent length and time scales

c) proportional to the product of turbulent length and velocity scales

Express the turbulence length scale in terms of k and ε.

a)(\frac{k}{\epsilon})^{\frac32}

b)(\frac{k^{\frac32}}{\epsilon})

c)(\frac{\epsilon}{k^{\frac32}})

d)(\frac{\epsilon}{k})^{\frac32}

b)(\frac{k^{\frac32}}{\epsilon})

Which of the following model is not an eddy viscosity turbulence model?

a) Standard k-e model,

b) Mixing length model

c) Reynolds stress model

d) K-omega SST model

c) Reynolds stress model.

Wall function can be used when the first node satisfies ___________.

a) y+ < 1

b) 1< y+ < 30

c) 30 < y+ < 300

d) y+ > 300

c) 30 < y+ < 300

Which of these properties is not ensured in Finite Difference Methods?

a) Stability

b) Convergence

c) Conservativeness

d) Accuracy.

c) Conservativeness

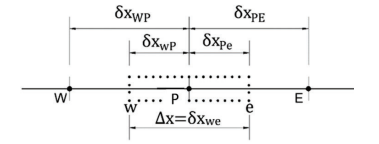
Consider the following stencil.

The discretized form of

(d\phi/dx)_{w}

using the central differencing scheme is:

a)\dfrac{\phi_{P}+\phi_{W}}{\delta x_{WP}}

b)\dfrac{\phi_{P}-\phi_{W}}{2}

c)\dfrac{\phi_{P}-\phi_{W}}{\delta x_{WP}}

d)\dfrac{\phi_{P}+\phi_{W}}{2}

c)\dfrac{\phi_{P}-\phi_{W}}{\delta x_{WP}}

The numerical convection schemes should be _________.

a) upwind biased

b) downwind biased

c) upwind or downwind depending on the problem

d) considering both upwind and downwind equally

a) upwind biased

The diagram below represents a one-dimensional mesh with vertical lines representing the control volume faces. The conservation equations are applied to which of these points while discretizing the equation using the Finite Volume Method?

5, 6, 7

Select the correct statement.

a) Explicit method is unconditionally stable.

b) Explicit method requires no iterations and hence cheap to run.

c) Explicit method requires CFL (Courant-Friedrichs-Lewy number) > 1.

d) Explicit method is second order accurate.

b) Explicit method requires no iterations and hence cheap to run.

The pressure correction equation is used to ensure _________.

a) energy conservation

b) velocity conservation

c) momentum conservation

d) mass conservation

d) mass conservation

If the simulation oscillates and hence does not converge, which of the following actions cannot be used to overcome this problem?

a) Reducing relaxation factors

b) Checking mesh quality

c) Reducing convergence tolerance

d) Using an improved initial flow

c) Reducing convergence tolerance.

Which of the following traits is not a measure of the quality of mesh?

a) Aspect ratio

b) Order of accuracy

c) Smoothness

d) Skewness.

b) Order of accuracy

If the tolerance value to stop the iteration is too big, which of these properties will be affected?

a) Accuracy

b) Efficiency

c) Stability

d) Conservativeness

a) Accuracy

What is the physical meaning of the local derivative?

(a) The time rate of change following a moving fluid element.

(b) The time rate of change at a fixed point.

(c) The time rate of change due to the movement of the fluid element from one location to another in the flow field where the flow properties are spatially different.

(d) None of the above.

(b) The time rate of change at a fixed point.

Select the correct answer that mathematically describes a three-dimensional incompressible flow, steady state or transient.

a)\frac{\partial\rho}{\partial t}+\left[\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}\right]=0

b)\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0

c)\frac{\partial u_i}{\partial x_i}=0,\quad i=1,2

d)\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0

b)\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0 , Steady State

What is the Stokes relationship?

(a) Relationship between inertial and viscous forces.

(b) Relationship between surface and volumetric forces.

(c) Relationship between viscous stresses, and velocity gradients.

(d) Relationship between pressure and viscosity.

(c) Relationship between viscous stresses, and velocity gradients.

Consider the flow of an incompressible fluid between two infinite horizontal parallel plates placed at y=0 and y=H. The plates are fixed and the flow is driven by a constant pressure gradient in the streamwise direction − 𝑑𝑝/𝑑𝑥 = 𝐺 > 0. The laminar velocity profile inside the channel is given by 𝑢(𝑦) = 𝐺/2𝜇 𝑦(𝐻 − 𝑦). What is the correct expression for the shear stress (𝜏) at the centerline?

a)\tau=\mu\frac{GH}{2}

b)\tau=-\frac{GH}{2\mu}

c)\tau=\frac{GH}{2\mu}

d)\tau=0

d)\tau=0

What is the definition of 𝑢 +?

a) The ratio of the friction velocity to velocity normal to the wall

b) The ratio of velocity normal to the wall to the friction velocity

c) The ratio of the friction velocity to velocity parallel to the wall

d) The ratio of velocity parallel to the wall to the friction velocity

d) The ratio of velocity parallel to the wall to the friction velocity

What is Reynolds stress?

a) Stress due to velocity fluctuations

b) Tangential component of pressure

c) Stress due to pressure fluctuations

d) Normal component of viscosity

a) Stress due to velocity fluctuations

What do k and ε stand for?

a) Turbulent kinetic energy and its dissipation rate per unit mass

b) Turbulent kinetic energy and turbulent diffusivity

c) Turbulent diffusivity and its dissipation rate per unit mass

d) Turbulent kinetic energy and mass transfer

a) Turbulent kinetic energy and its dissipation rate per unit mass

Express the turbulence velocity scale in terms of k and ε.

a)\quad\epsilon^{1/2}

b)\quad\left(\frac{\epsilon}{k}\right)^{1/2}

c)\quad k^{1/2}

d)\quad\left(\frac{k}{\epsilon}\right)^{1/2}

c)\quad k^{1/2}

Let Cμ be a dimensionless constant and ρ be the density of the flow. Express the dynamic eddy viscosity in terms of turbulence kinetic energy (k) and a turbulence time scale (𝜏).

a)\quad\frac{\rho C_{\mu}k^2}{\tau}

b)\quad\frac{\rho C_{\mu}k}{\tau}

c)\quad\rho C_{\mu}k\tau

d)\quad\frac{\rho C_{\mu}\tau^2}{k}

c)\quad\rho C_{\mu}k\tau

The Reynolds stress turbulence model is particularly useful if the flow is:

a) Separated from the surface

b) Dominated by swirl

c) Three-dimensional

d) Unsteady

b) Dominated by swirl

Select the incorrect statement.

a) The low-Reynolds number model requires no wall function.

b) The low-Reynolds number model is for low-Reynold number flow only.

c) The low-Reynolds number model requires 𝑦 + < 1.

d) The low-Reynolds number model considers viscous effect near the wall.

b) The low-Reynolds number model is for low-Reynold number flow only.

Which of these is an advantage of the Finite Difference Method over the Finite Volume Method?

a) Conservativeness

b) Higher-order

c) Stability

d) Complex problems

b) Higher-order

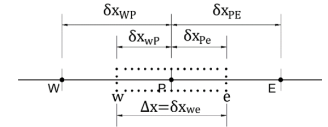
Consider the following stencil.

The discretized form of (𝑑𝜙/𝑑𝑥)𝑒 using the central differencing scheme is:

a)\quad\frac{\phi_{P}+\phi_{E}}{\delta x_{PE}}

b)\quad\frac{\phi_{E}-\phi_{P}}{2}

c)\quad\frac{\phi_{E}-\phi_{P}}{\delta x_{PE}}

d)\quad\frac{\phi_{P}+\phi_{E}}{2}

c)\quad\frac{\phi_{E}-\phi_{P}}{\delta x_{PE}}

The numerical convection schemes are often upwind biased for_________.

a) Higher accuracy

b) Better stability

c) Low numerical diffusion

d) Ease of calculation

b) Better stability

The number of discretized equations is equal to the number of __________.

a) Discretized internal cells

b) Boundary conditions

c) Unknowns

d) Boundary-side elements

a) Discretized internal cells

The CFL number should normally be kept

a) >1

b) <1

c) >10

d) <10

b) <1

The SIMPLE algorithm is a ____________.

a) Weighted average method

b) Predictor-corrector method

c) Euler method

d) Newton method

b) Predictor-corrector method

CFD packages solve the algebraic equations of flow using ____________ method.

a) Direct

b) Analytical

c) Trial and error

d) Iterative

d) Iterative

The aim of the mesh independence study is to understand the

a) Effect of turbulence model

b) Convergence of iteration

c) Effect of mesh resolution

d) Effect of convection schemes

c) Effect of mesh resolution

A solution is ideally converged if _________.

a) the results match with the exact solution

b) the results for two consecutive iterations are the same

c) the residuals fall below some pre-set criterion

d) the results for different boundary conditions are the same

c) the residuals fall below some pre-set criterion

What is the difference between Newtonian and non-Newtonian fluids?

• Newtonian: Constant viscosity; shear stress ∝ shear rate (e.g. water, air).

• Non-Newtonian: Variable viscosity; does not follow Newton’s law (e.g. ketchup, blood)

Compressible vs. Incompressible Flow

• Compressible: Density changes significantly (e.g. high-speed gas).

• Incompressible: Density is constant (e.g. liquid flow, low-speed air).

What are the different engineering approaches available to analyse a fluid problem and which approach is the most useful one?

• Analytical: Exact math solutions; only for simple cases.

• Experimental: Real-world testing; accurate but costly.

• CFD: Computer simulation; flexible and widely used.

Most Useful: CFD, for complex, cost-effective, and fast analysis.What is CFD?

What is CFD?

Computational Fluid Dynamics: A numerical method to simulate fluid flow using computers by solving discretized fluid equations.

First Step in CFD & Importance

• Step: Geometry creation + meshing.

• Importance: Defines the physical domain; affects accuracy and computation time.

Physical Principles in Fluid Analysis

• Mass conservation

• Momentum conservation (Newton’s 2nd Law)

• Energy conservation (First Law of Thermodynamics

What is a closed or analytical solution of a set of equations?

• Definition: Exact solution expressed in mathematical form (e.g. formula).

• Used for: Simple geometries and flows.

Mathematical vs. Numerical Model

• Mathematical: Uses equations to represent physical laws.

• Numerical: Solves those equations approximately using discretization.

Why is CFD considered a ‘compromise’ between having, or not having a solution of the Navier-Stokes equations?

Why: Navier-Stokes equations are too complex for exact solutions in most cases—CFD gives an approximate but practical solution.

Eulerian vs. Lagrangian Approach

• Eulerian: Observes fluid flow at fixed points in space.

• Lagrangian: Follows individual fluid particles through space and time.

What is the physical meaning of the total derivative when quantifying a change in a fluid variable such as temperature? In this context, what is the physical meaning of the local and convective derivatives?

• Meaning: Tracks how a quantity (e.g. temperature) changes for a moving fluid element.

• Local Derivative: Change at a fixed point (∂/∂t).

• Convective Derivative: Change due to movement through space (u·∇T).

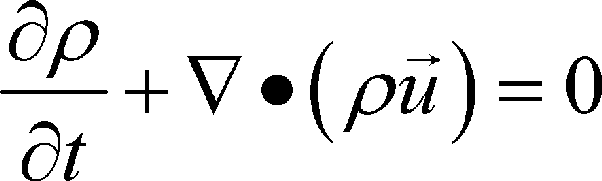
What do the various terms in the continuity equation mean physically?

• ∂ρ/∂t: Rate of density change at a point.

• ∇·(ρu): Net mass flow out of a point.

• Equation: Ensures mass is conserved.

Why Use Conservation of Mass Equation?

Reason: Guarantees mass isn’t created or lost; essential for realistic fluid modeling.

Can you think about another example, where the monitored variable is velocity, to explain the physical meaning of the substantial (or total) derivative?

If fluid velocity increases as a particle moves, the total derivative of velocity shows acceleration—a combo of local and convective changes.

What is the physical meaning of velocity field with divergence zero in the incompressible case?

Meaning: Volume of fluid elements doesn’t change; no net inflow/outflow—mass is conserved with constant density.

Which of the following mathematically describe a 3D, steady-state, compressible flow?

a)\frac{\partial(\rho u)}{\partial x}+\frac{\partial(\rho v)}{\partial y}+\frac{\partial(\rho w)}{\partial z}=0

b)\frac{\partial\rho}{\partial t}+\left(\frac{\partial(\rho u)}{\partial x}+\frac{\partial(\rho v)}{\partial y}\right)=0

c)\nabla\cdot(\rho\vec{V})=0

d)\nabla\cdot\vec{V}=0

a) and c)

(steady state:not time dependant, compressible:function of density, 3D)

Which of the following describe a 3D, incompressible flow (steady or transient)?

a)\frac{\partial\rho}{\partial t}+\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}\right)=0

b)\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0

c)\frac{\partial u_i}{\partial x_i}=0,\quad i=1,2

d)\nabla\cdot(\rho\vec{V})=0

b)

(incompressible:density is constant)

Which of the following describe a 2D, incompressible flow (steady or transient)?

a)\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0

b)\frac{\partial u_i}{\partial x_i}=0,\quad i=1,2

c)\nabla\cdot\vec{V}=\text{div}\vec{V}=0

d)\frac{\partial\rho}{\partial t}+\left(\frac{\partial(\rho u)}{\partial x}+\frac{\partial(\rho v)}{\partial y}\right)=0

a), b), c)

(incompressible:no density)

Which of the following describe a 2D, transient, compressible flow?

a)\frac{\partial(\rho u_i)}{\partial x_i}=0,\quad i=1,2

b)\frac{\partial\rho}{\partial t}+\nabla\cdot(\rho\vec{V})=0

c)\frac{\partial\rho}{\partial t}+\left(\frac{\partial(\rho u)}{\partial x}+\frac{\partial(\rho v)}{\partial y}\right)=0

d)\frac{\partial\rho}{\partial t}+u\frac{\partial\rho}{\partial x}+v\frac{\partial\rho}{\partial y}+\rho\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right)=0

b), c), d)

(a) implies steady flow not transient)

Write the continuity equation in tensor (Einstein) notation and in vector form.

Given (standard form):

\displaystyle \frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \vec{u}) = 0

Tensor (Einstein) notation:

{\displaystyle\frac{\partial\rho}{\partial t}+\frac{\partial(\rho u_i)}{\partial x_i}=0} where x1=x x2=y x3=zu1=u u2=v u3=w

Vector form:

\displaystyle \frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \vec{u}) = 0

Show that the continuity equation in conservation form is equivalent to the non-conservation form using tensor notation.

Conservation form (tensor):

\displaystyle \frac{\partial \rho}{\partial t} + \frac{\partial (\rho u_i)}{\partial x_i} = 0

use product rule:

\displaystyle \frac{\partial (\rho u_i)}{\partial x_i} = u_i \frac{\partial \rho}{\partial x_i} + \rho \frac{\partial u_i}{\partial x_i}

Sub into original equation:

\displaystyle \frac{\partial \rho}{\partial t} + u_i \frac{\partial \rho}{\partial x_i} + \rho \frac{\partial u_i}{\partial x_i} = 0

Group terms:

\frac{D \rho}{D t} + \rho \nabla \cdot \vec{u} = 0

Which gives the non-conservation form (substantial derivative):

\frac{D \rho}{D t} + \rho \nabla \cdot \vec{u} = 0

What types of forces can act on a fluid element?

• Body forces (e.g. gravity, electromagnetic)

• Surface forces:
   • Normal stresses (pressure + viscous)
   • Shear stresses (viscous only)

What are the Stokes relationships?

They relate normal viscous stresses to shear viscosity in Newtonian fluids, assuming zero bulk viscosity:

\tau_{xx} = 2\mu \frac{\partial u}{\partial x} - \frac{2}{3} \mu \nabla \cdot \vec{u}

similar for \/

\tau_{yy}, \tau_{zz}

What variables influence shear or normal stresses?

• Velocity gradients

• Fluid viscosity

• For compressible flow: bulk viscosity and divergence of velocity

How many momentum equations should you use in your fluid problem?

One per spatial dimension (e.g. 2D → 2 equations, 3D → 3 equations).

Why is the substantial derivative needed in momentum equations?

Because it accounts for changes due to both time and fluid motion:

\frac{D\vec{u}}{Dt} = \frac{\partial \vec{u}}{\partial t} + (\vec{u} \cdot \nabla) \vec{u}

In fully developed flow in a straight cylinder along x, are

\frac{\partial u}{\partial x},\frac{\partial u}{\partial y}

significant.

\frac{\partial u}{\partial x} = 0

flow is fully developed

\frac{\partial u}{\partial y} \neq 0

velocity varies radially

When should I consider body forces?

When gravity or external fields (e.g. EM) significantly affect flow behavior.

When should I consider normal stresses?

In compressible or high-speed flows where pressure/viscous stresses are non-negligible.

When should I consider shear stresses?

In viscous flows, near walls, or at low Reynolds numbers.

When do we need to use the energy equation?

When temperature affects flow (compressible, thermal convection, or high-speed flows).

Why do we specify boundary conditions in CFD?

To close the system of PDEs and ensure a unique, physically meaningful solution.

Can we solve the Navier-Stokes equations analytically? Justify.

Rarely. Only for simple, idealized cases. They are nonlinear and coupled.

Why are the Navier-Stokes equations difficult to solve analytically?

Due to nonlinearity from the convective term and complex geometries/boundary conditions.

What does “fully developed flow” mean?

Velocity profile no longer changes in the flow direction;

\frac{\partial \vec{u}}{\partial x} = 0

find: a) volumetric flow rate b) wall shear stress at y=0 for

u(y) = \frac{G}{2\mu} y(H - y)

a)

Q = \int_0^H u(y) , dy = \frac{G H^3}{12 \mu}

b)

\tau_w = \mu \left.\frac{du}{dy}\right|{y=0} = \mu \cdot \frac{G}{2\mu}(H - 2y) \big|{y=0} = \frac{G H}{2}

What is the difference between laminar and turbulent flow

• Laminar: smooth, orderly layers

• Turbulent: chaotic, vortical, energy cascade

What are main features of turbulent flow?

• Irregularity

• Vorticity

• Diffusivity

• 3D and time-dependent

• Energy cascade

Why examine inertial vs. viscous forces?

It defines the flow regime via Reynolds number:

\text{Re} = \frac{\rho U L}{\mu}

What other factors influence turbulence?

• Geometry

• Surface roughness

• External forcing

• Initial/boundary conditions

Differences between DNS, LES, and RANS?

• DNS (Direct numerical simulation): resolves all scales (costly)

• LES (large eddy sim): resolves large scales, models small

• RANS (Reynolds averaged Navier Stokes): averages all scales, uses turbulence models

Limitations of RANS and LES models?

• Depend on empirical models

• May fail in complex flows or near-wall regions

• LES still computationally expensive

What is the law of the wall? Why “universal”?

Describes velocity near walls in turbulent flows:

u^{+}=\frac{1}{\kappa}\ln y^{+}+Bu^{+}=\frac{1}{\kappa}\ln y^{+}+B

"Universal" because it fits many flows if non-dimensionalized

How are u+ and y+ defined and interpreted?

u^+ = \frac{u}{u_\tau}

y^+ = \frac{y u_\tau}{\nu}

They represent velocity and distance scaled by wall shear.

How fine should your mesh be to resolve the viscous sublayer?

First cell center at

y^+ \leq 1

otherwise use wall functions

What are the differences between Navier-Stokes and Reynolds Averaged Navier-Stokes (RANS) equations?

Navier-Stokes equations describe instantaneous flow variables, while RANS equations describe time-averaged variables and include Reynolds stresses due to turbulence:

\overline{u_{i}u_{j}}\neq\overline{u}_{i}\,\overline{u}_{j}\Rightarrow-\overline{u_{i}^{\prime}u_{j}^{\prime}}

(Reynolds stresses)

What do we mean by linear and non-linear terms in the momentum equations?

Linear terms: involve single velocity components (e.g., ∂u/∂x)
Non-linear terms: involve products of velocities (e.g., u ∂u/∂x)

Main steps to derive the RANS momentum equations?

1st Decompose:

u = \overline{u} + u'

2nd Time-average Navier-Stokes

3rd Apply time-averaging rules

4th Introduce Reynolds stresses:

- \rho \overline{u_i' u_j'}

Where do Reynolds stresses come from?

They arise from time-averaging nonlinear convective terms.
Physically, they represent turbulent momentum transfer and must be modeled.

Why must CFD results be validated?

Model assumptions (e.g., turbulence closure) can deviate from reality. Validation ensures reliability.

Prove the time averaging rule:

\overline{a'b'} = \overline{ab} - \overline{a} \,\overline{b}

Let

a=\overline{a}+a^{\prime},b=\overline{b}+b^{\prime}

Then

ab=\overline{a}\,\overline{b}+\overline{a}b^{\prime}+\overline{b}a^{\prime}+a^{\prime}b^{\prime}

Time Average:

\overline{ab} = \overline{a}\,\overline{b} + \overline{a' b'}

—>

\overline{a' b'} = \overline{ab} - \overline{a} \,\overline{b}

Reynolds averaging of:

∂(u_j u_i)/∂x_j ?

\overline{\partial (u_j u_i)/\partial x_j} = \partial/\partial x_j (\overline{u}_j \, \overline{u}_i + \overline{u_j' u_i'}) Turbulence stress arises as:

∂ \overline{u_j' u_i'} / ∂x_j

What is the Boussinesq Hypothesis (1877)?

Boussinesq's hypothesis assumes that the turbulent (or eddy) shear stresses in a fluid can be modeled in a manner analogous to the viscous stresses in laminar flow, using an eddy viscosity (also called turbulent viscosity).

It allows closure of the Reynolds-Averaged Navier-Stokes (RANS) equations by modelling Reynolds stresses as:

- \overline{u_i' u_j'} = \nu_t \left( \frac{\partial \overline{u}_i}{\partial x_j} + \frac{\partial \overline{u}_j}{\partial x_i} \right)

Differences between Navier-Stokes, RANS, and EVM RANS?

• Navier-Stokes: Instantaneous, no modeling

• RANS: Time-averaged, includes Reynolds stresses

• EVM-RANS: Uses eddy viscosity (νt) to model Reynolds stresses

How is each term in the k equation treated?

• Production: Modeled

• Dissipation: Modeled

• Convection: Exact

• Diffusion: Modeled

Physical meaning of k and ε equation terms?

• k : Turbulent kinetic energy

• ε : Rate of dissipation of k
  Terms model generation, transport, and loss of turbulence energy.

Why is CFD validation important?

Simulations use assumptions and models that may not reflect real flows. Validation ensures accuracy.

Eddy viscosity based on k and turbulence timescale τ ?

\nu_t = C_\mu k \tau

How are model constants determined?

By fitting to experimental data or DNS in canonical cases like flat plates, pipe flows, etc.

Mixing length model (Nikuradse form)?

\left(\nu_{t}=l_{m}^2\left|\frac{\partial U}{\partial y}\right|l_{m}/R=0.14-0.08(1-y/R\right)^2-0.06\left(1-y/R)^4\right)