Experiment Errors

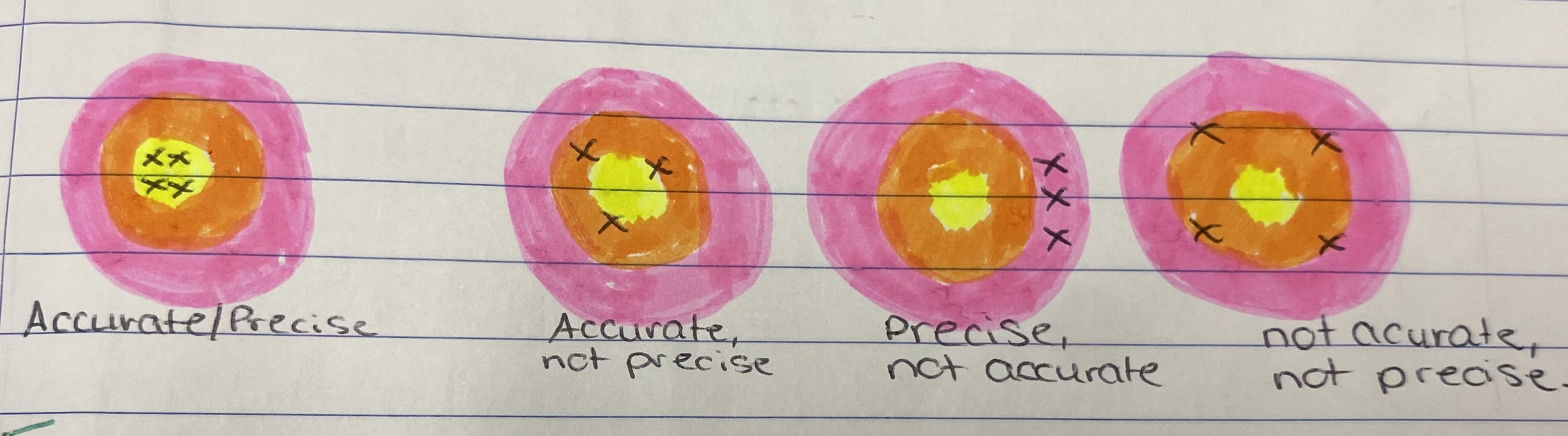
Accuracy and precision:

Precision is how close repeated measurements are to each other. Precise measurements are clustered closely together.

Accuracy is how close a measured value is to the true value of the quantity being measured. Accurate measurements are clustered around the correct value.

There are two types of error. Systematic error: three examples of systematic error-

Due to instrumentation : eg: incorrect calibration of an electric balance. Eg: an analogue anmetre may point to slightly below 0 when there is no current.

Due to person not using correct procedure: eg: parallax error.

Due to limitations in the design of the experiment: eg: measuring the temperature rise of water being heated by a coil- some heat will be lost in the environment.

Effects of systematic errors: ( 4 effects)

Can cause all measurements to be too high or too low.

Cannot be reduced or eliminated by repeated trials.

Reduced accuracy.

Do not necessarily affect permission.

How do reduce/ minimise systematic errors:

Ensuring correct calibration

Following the correct method of use of instrument

Taking measures to counteract or to allow for these errors

Random Errors- ( 2 examples of random errors)

Due to instrumentation: eg: electric balance can be effected by air currents high might give different air currents which might give different (slightly) readings each time. Eg: fluctuation of room temperature could affect how an instrument behaves.

Caused by a person making the measurement: eg: the person uses or reads the instrument slightly different each time. Eg: human reaction time could cause variations when stopping or starting a stopwatch.

Effects of random errors:

Unpredictable and inconsistent variations in the value of repeated measurements - some will be too high and others too low.

May not necessarily affect accuracy.

Will affect precision.

How can we reduce/ minimise random error?

Taking several measurements and getting an average ( ignore extreme values/ outliers)

Drawing a graph if possible.

Following the correct method of use of an instrument.

Percentage errors- True Vale known:

Error= true value - estimate

Percentage error= error/ true value (actual) x 100

Percentage error- true value not known:

Percentage error= estimate error/ measured value x 100

Estimate error= smallest division on the scale/ 2

Eg: a smallest division on a metre stick is 1mm so estimated error is 0.5mm or 0.0005m so all readings will be incorrect by + or - 0.005m.