Unit 2: Differentiation: Definition and Fundamental Properties

Rates of Change

We know that there are two ways of finding the rate of change

• We can use the difference quotient to find the Average Rate of Change

• The difference quotient is the rate of change over an interval of time

  A simpler way of saying this is y2 - y1/x2-x1

• The other way of finding the rate of change is at a specific point in time and this is called the Instantaneous Rate of Change

• This is the difference quotient but with a limit as h → 0

Slopes of Lines and Definition of Derivative

• Let's say we had a line that isn't linear, and we want to find the slope

• For a linear line, the slope is "rise over run" but we can't do that for a curved line

• Therefore we have to use the secant line to approximate the slope

  We can find the slope of the secant line using the difference quotient!

  (Look at the formula below)

• The closer the points are, the more accurate this slope will be

• Therefore we can use a different kind of line- the tangent line- that touches the curve at exactly one point

• We get this line by using the Instantaneous Rate of Change (remember: the difference quotient but with a limit as h → 0)

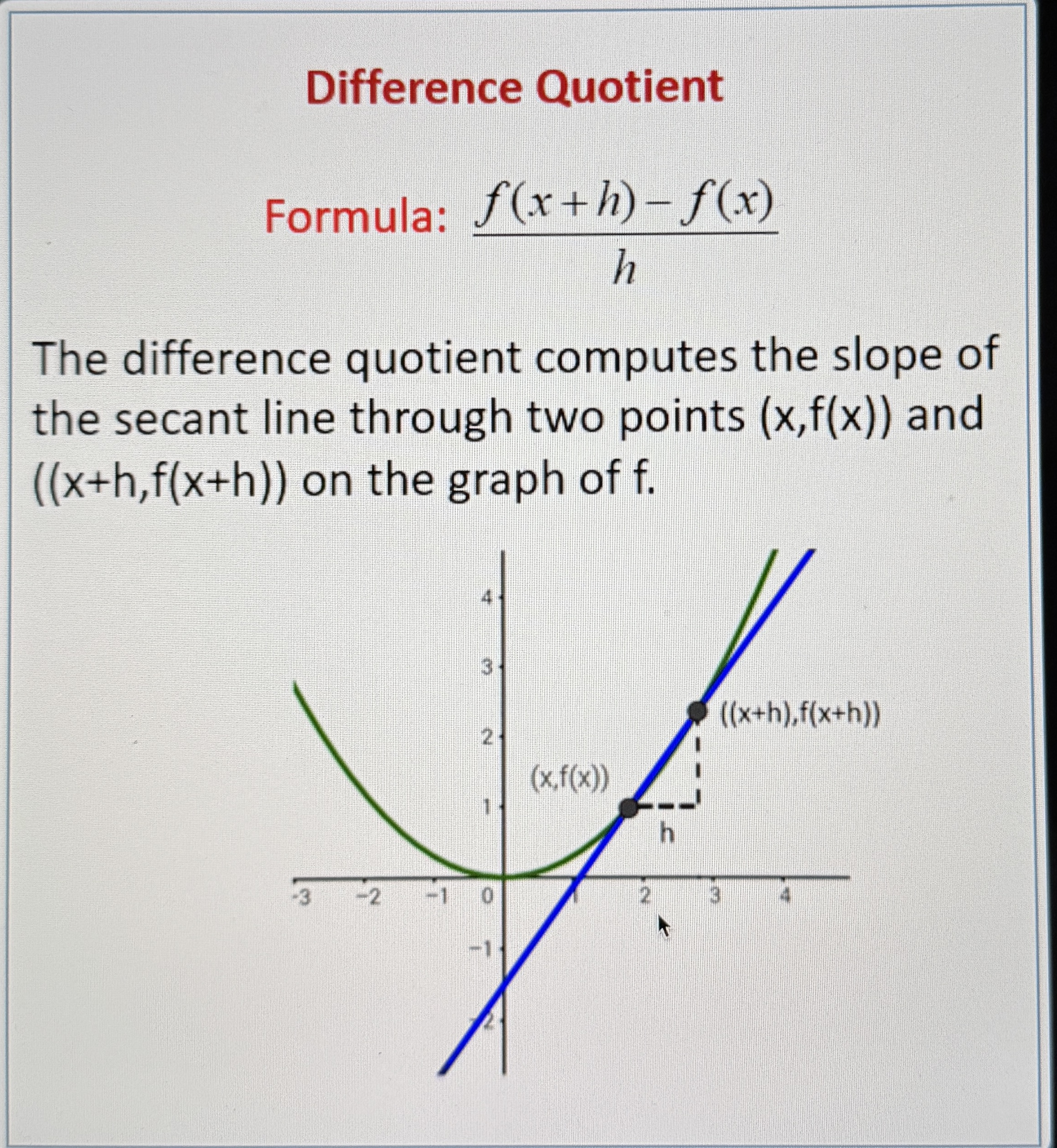
The Definition of a Derivative

This is called the definition of the derivative!

• Remember that the derivative is just the rate of change at a specific point, so we use a limit to find the slope as x gets infinitesimally small

Derivative Notations

Ex.

Constant Rule

Constant Rule: If f(x) = k where k is a constant then f’(x) = 0

• Ex. f(x) = 10 so f’(x) = 0

Constant Multiple Rule

Constant Multiple Rule: If you have a constant multiplied by a function, you can
"pull the constant out"

• So [k* f(x)] would be the same as k * f’(x)

The Power Rule

The Power Rule: If f(x) = x^n then f’(x) = nx^n-1

• For example x^4 becomes 4x^3 and 2x^2 would be 4x

• A good way to describe this rule is to "multiply down and decrease the power"

• The power rule works for polynomials!

The Product Rule

The Product Rule: If you have two polynomials multiplied by each other like (2x +7)(9x + 8) you could multiply it out and then use the power rule, but this takes time, so we have something called the product rule.

• The product rule says that if f(x) = uv then f’(x) = (u)(dv/dx) + (v)(du/dx)

• You take the first term and multiply it by the derivative of the second term (using the power rule) then add that to the second term multiplied by the derivative of the first term

• The way I learned it was "1d2 + 2d1" (first derivative of second + second derivative of the first)

The Quotient Rule

The Quotient Rule: If you need to take the derivative of a fraction, you have to use this rule

• The Quotient Rule says that if f(x) = u/v then f’(x) = (v)(du/dx) - u(dv/dx) /v12

• You take the denominator and multiply it by the derivative of the numerator, then subtract the numerator multiplied by the derivative of the denominator all over the denominator squared

• The way I learned it was "low d high - high d low/ low*2" (low derivative of high - high derivative of low over low^2)

Differentiation Rules

Ex.

Other Derivatives

Ex.

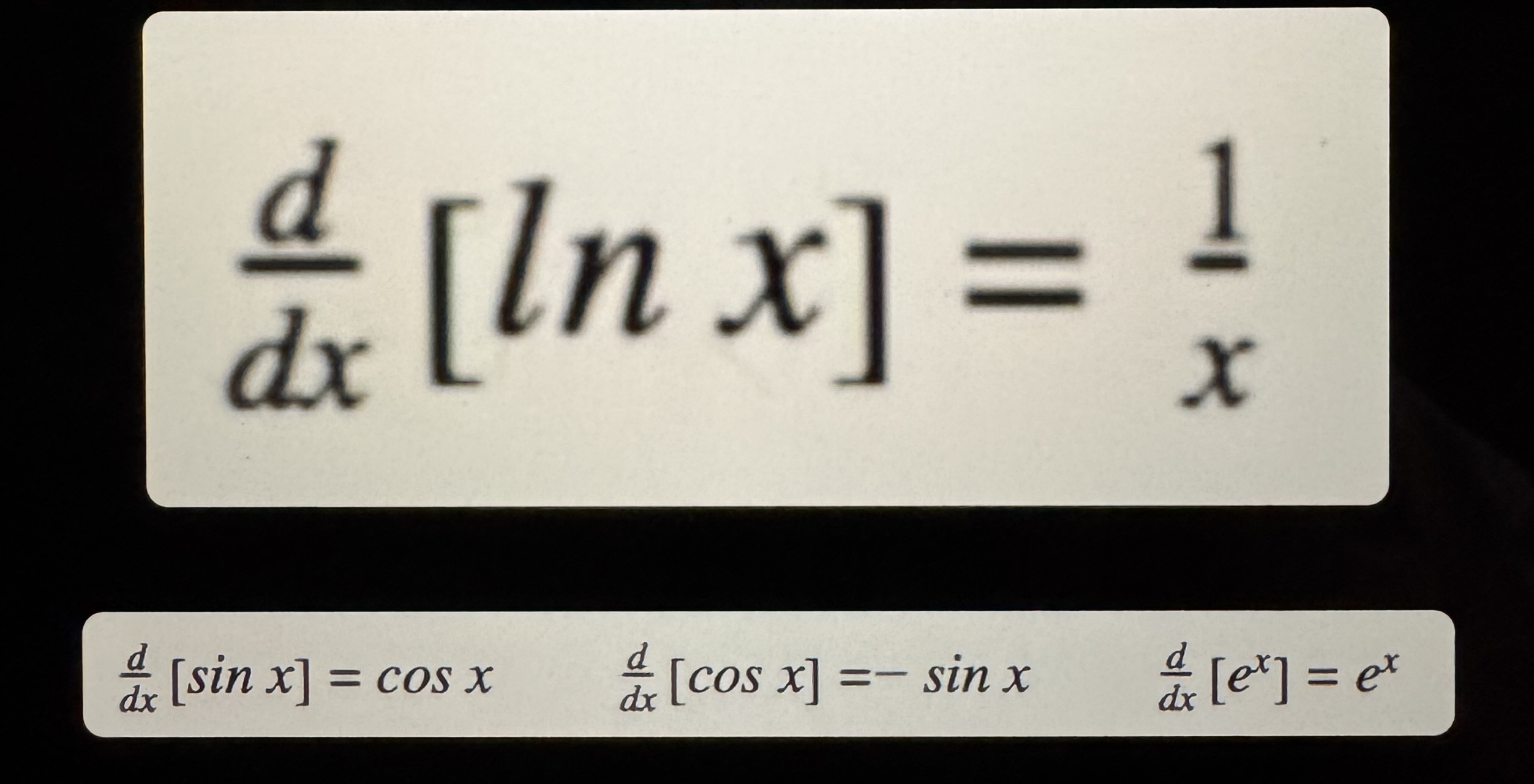
Definition of a Derivative #1

Ex.

Definition of a Derivative #2

Ex.

Basic Differentiation Rules #1

Ex.

Basic Differentiation Rules #2

Ex.

Tangent Lines and Horizontal Tangents #1

Ex.

Tangent Lines and Horizontal Tangents #2

Ex.

Rates of Change #1

Ex.

Rates of Change #2

Ex.

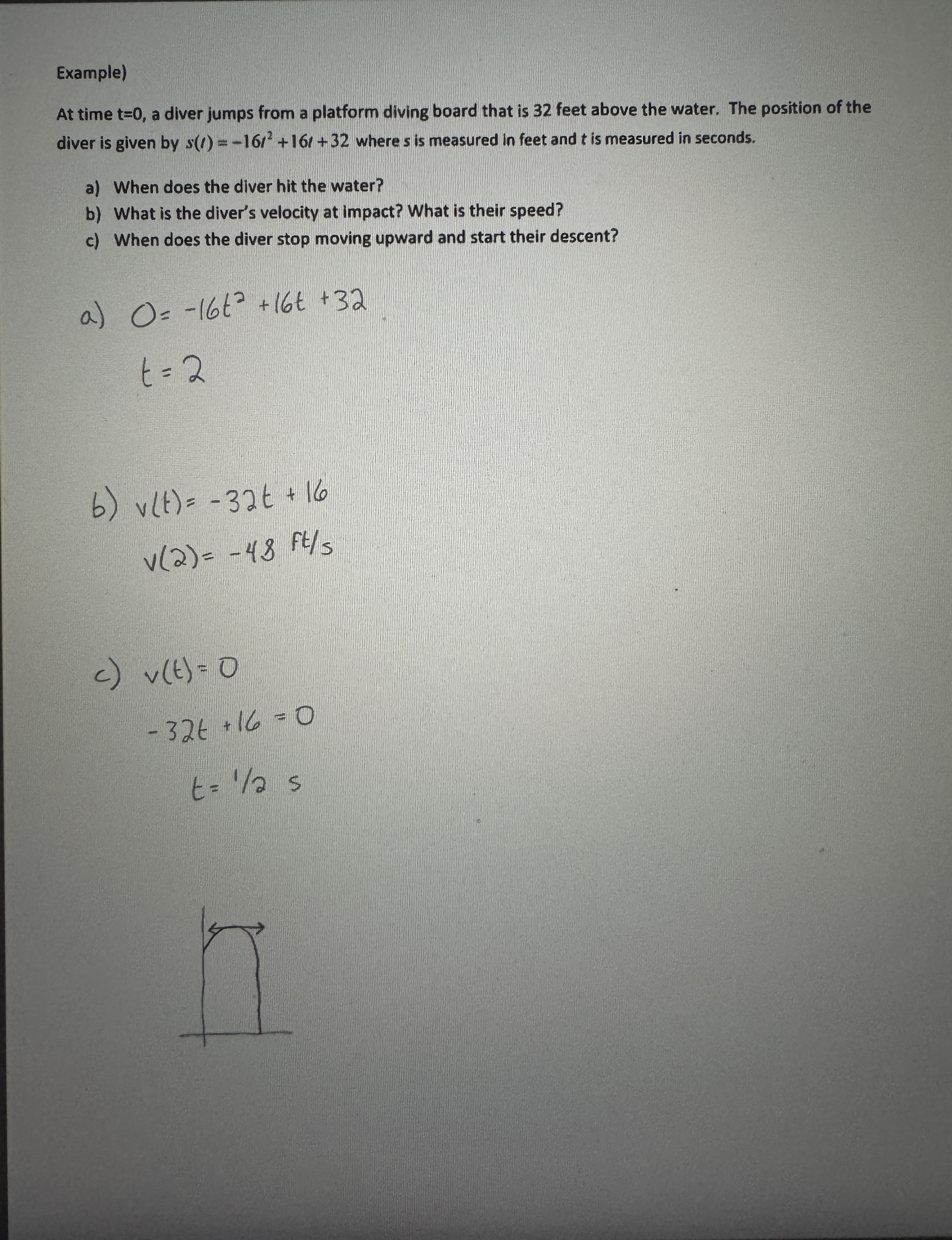
Higher Order Derivatives and Product Rule #1

Ex.

Higher Order Derivatives and Product Rule #2

Ex.

Quotient Rule and Trig Derivatives #1

Ex.

Quotient Rule and Trig Derivatives #2

Ex.

Chain Rule #1

Ex.

Chain Rule #2

Ex.

Chain Rule Part 2 and Absolute Value #1

Ex.

Chain Rule Part 2 and Absolute Value #2

Ex.

Implicit Differentiation #1

Ex.

Implicit Differentiation #2

Ex.

Related Rates #1

Ex.

Related Rates #2

Ex.

Related Rates #3

Ex.

Related Rates #4

Ex.