Maximum and Minimum Values of Functions

These flashcards cover the key concepts regarding maximum and minimum values of functions, critical numbers, and the methods used to find extrema.

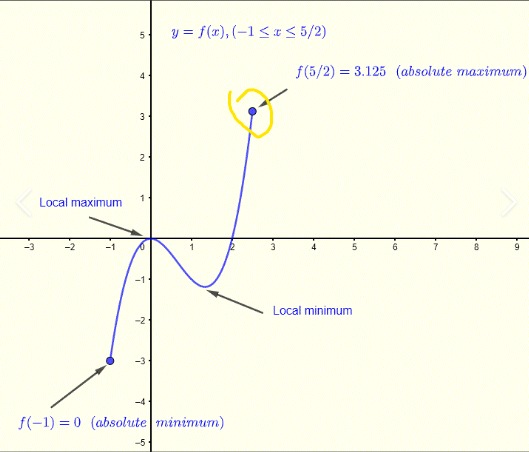
What is an absolute maximum of a function f at point c?

f(c) > f(x) for all x in the domain D.

What is an absolute minimum of a function f at point c?

f(c) < f(x) for all x in the domain D.

What are the maximum and minimum values of a function called?

The extreme values of the function.

Does every function have an absolute maximum and minimum?

No.

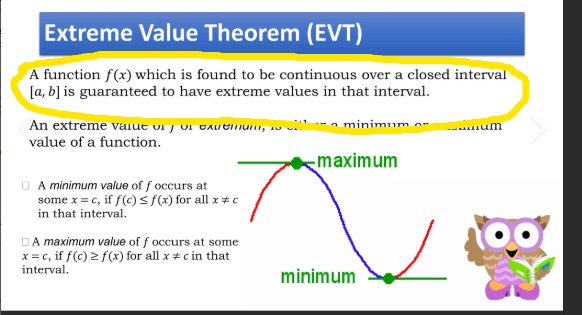
What does the Extreme Value Theorem state?

If f is continuous on a closed and bounded interval [a, b], then f attains both an absolute minimum and an absolute maximum on that interval.

How can we locate absolute extrema of functions?

By looking for local extreme values.

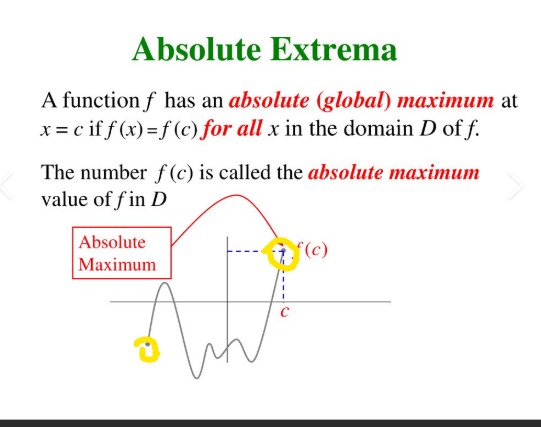
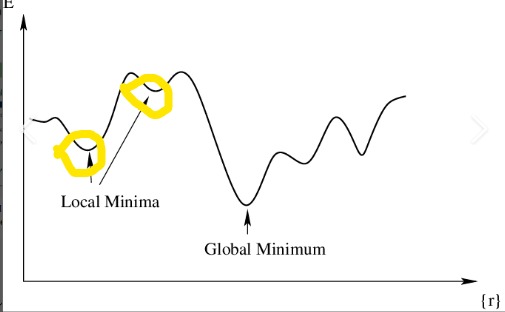
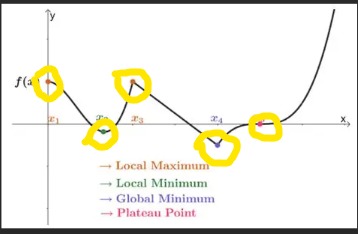
What defines a local maximum at c?

f(c) > f(x) for all x in a neighborhood around c.

What defines a local minimum at c?

f(c) < f(x) for all x in a neighborhood around c.

What is a critical number of a function f?

A number c in the domain where f'(c) = 0 or f'(c) is undefined.

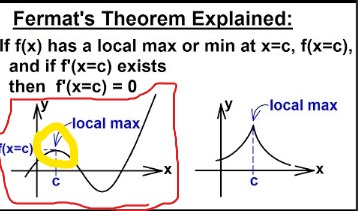
What does Fermat's Theorem state?

If f has a local maximum or minimum at c, and if f'(c) exists, then f'(c) = 0.

According to Fermat's Theorem, under what condition is c a critical number of f?

If f has a local maximum or minimum at c.

What is the procedure for finding absolute maximum or minimum values using the Closed Interval Method?

1. Find all critical numbers in [a, b]

2. Evaluate f at the critical numbers and endpoints.

3. Compare these values

What are the endpoints in the Closed Interval Method?

The values of the function at the borders of the interval [a, b].

In the example, what are the critical numbers of f(x) = 2x³ - 3x² - 12x + 5?

The critical numbers are -1 and 2.

How do we evaluate the function at critical numbers?

Find f values at the critical points and at the endpoints of the interval.

What is the significance of evaluating f at endpoints and critical numbers?

To find the absolute maximum and minimum over the interval.

What is meant by ‘absolute extrema’?

The absolute maximum or minimum values of a function.