Algèbre linéaire

rang

nombre de pivots quand on échelonne la matrice

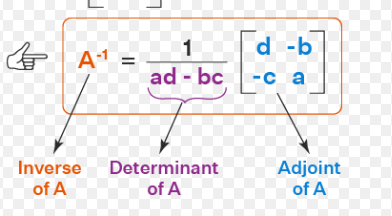
inverse d’une matrice 2×2

on peut organiser le calcul d’un déterminant en

développant par rapport à une ligne ou une colonne

alternance des signes (matrice 3×3 par ex)

mort/vie/mort

par l’opération Li←→Lj ou Ci ←→Cj det (A)=

-det(A)

par l’opération Li←→lambdaLj det(A)=

lambdadet(A)

par l’opération Li←→Li+lambdaLj det(A)=

inchangé

det(AB)=

det(A)det(B)

si rang(A)=n alors

déterminant différent de 0

méthode pour trouver la décomposition colonne-ligne

noter toutes les opérations élémentaires

on peut toujours exprimer un vecteur comme une combinaison linéaire de 2 autres vecteurs linéairement

indépendants

formule de changement de base

(v1’ v2’)=(v1 v2) P

formule de changement de coordonnées

[v]B’= P-1[v]B

une driote de R2 est un espace vectoriel généré par un

vecteur directeur

équation droite R2

α1x-α2y=0

équation de droite dans R3

x/α1=y/α2=z/α3

équation cartésienne de plan dans R3

v1x v2

droite affine de R2 et R3 caractérisées par

un point de départ et un vecteur directeur

équation de la droite affine R2

α2x-α1y= c (c à chercher)

équation droite affine R3

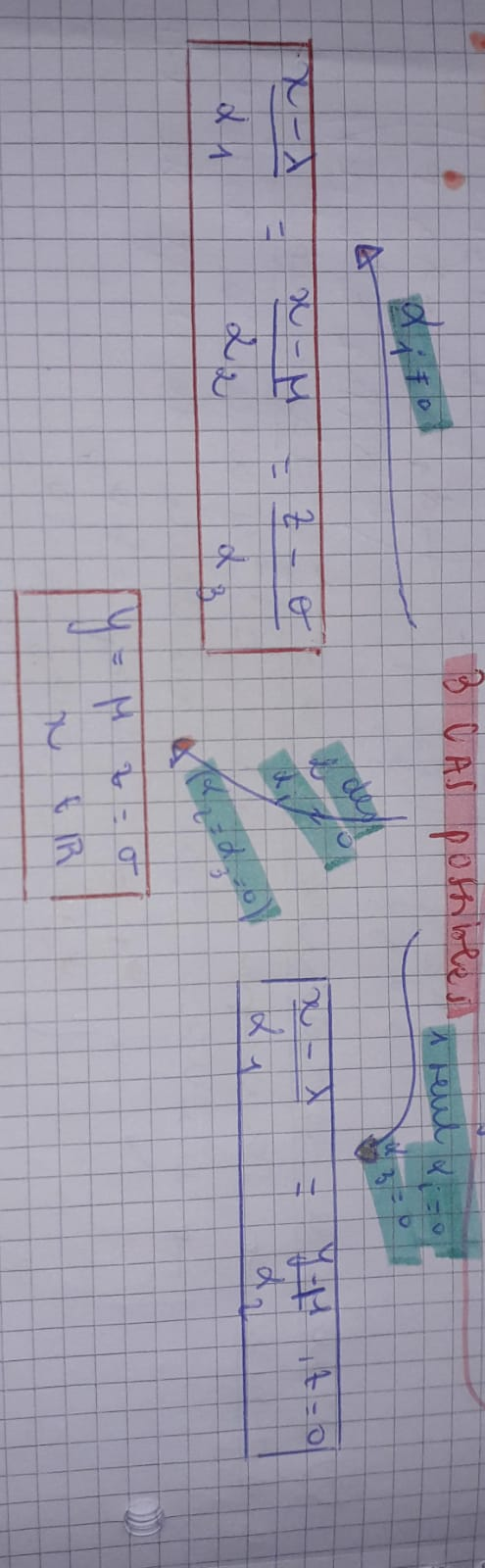
plans affines de R3

v0+vect(v1, v2)

équation cartesienne plans affines de R3

produit vectoriel