Lecture 04 - The Solow Growth Model in Continuous Time

Discrete Time Model

• Discrete time: t often starts at 0 or 1, but also could be an empirical date like 1990.

• In growth models, a time period is typically a year, but could be longer.

• In business cycle models, a time period is typically a quarter, but could be shorter.

Continuous Time

Simple discrete time model

discrete-time capital accumulation example

• If δ=0: capital grows without bound.

• If 0<δ<1: capital converges to a steady level where investment equals depreciation

Stock vs Flow variables

• 𝑘𝑡 is a stock variables, that is, it has a positive value at a single point in time, for example, August 15 2023 at 1PM.

• Investment, savings, output are flow variables.

  • Their values equal to zero on August 15 2023 at 1PM exactly.

  • But their values would be positive over the month of August.

• What happens between decision points in a discrete-time model?

  • Strictly speaking, i.e., in terms of the math, nothing!

  • One can imagine that some processes like production and consumption occur during decision points (for the values of the input factors chosen at the last decision point as given). That is, decisions are made at the beginning of period a quarter, but production and consumption happen during the quarter.

  • Nevertheless, all these variables are dated t.

How does continuous time relate to discrete time, and how do differences become derivatives as the time interval shrinks?

• Continuous time can be thought of as a discrete-time model where the length of the time interval, Δt, goes to zero.

• The key idea is that variables adjust continuously over very small time intervals, rather than only at discrete dates.

Understanding dt in Continuous Time

How are growth rates defined in continuous time, and why are log derivatives used?

What is the continuous-time Solow capital accumulation equation, and how is the steady state defined?

How does the continuous-time Solow model describe capital dynamics and convergence?

What does the continuous-time Solow model imply about growth rates in and out of the steady state?

What are the key implications of the continuous-time Solow model for growth, convergence, and interpretation of high-growth episodes?

• High growth can occur during transition due to capital accumulation.

• Growth slows as diminishing returns to capital set in.

• Countries with similar fundamentals converge to the same steady state (conditional convergence).

• Observed rapid growth does not imply superior institutions or permanent productivity gains.

• Sustained long-run growth requires TFP growth, which is not explained by the basic Solow model.

4 key solow model equations

diagrams

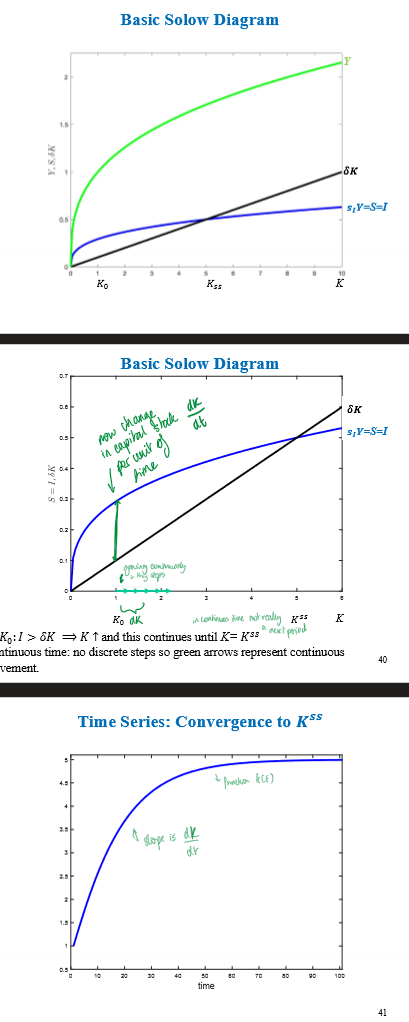
If theres a shock

A displays a discontinuous permanent jump

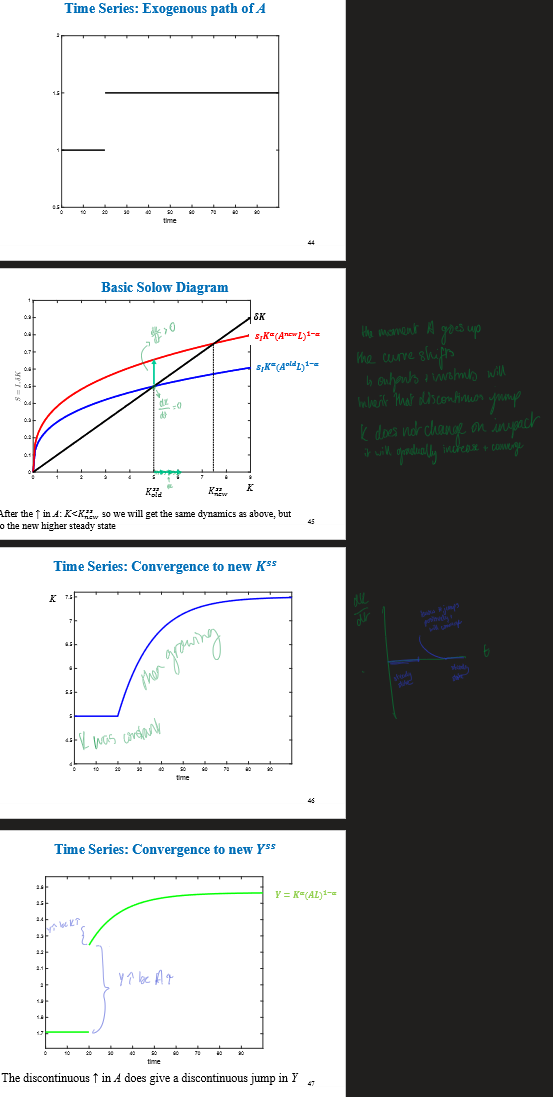
why no discontinuous jump in K

How does the continuous-time Solow model respond to a shock (e.g. to savings or capital), and what happens to growth during the transition?