Chapter 4: Discrete Random Variables

Introduction

• Random Variable Notation: Upper case letters such as X or Y denote a random variable. Lowercase letters like x or y denote the value of a random variable

4.1 Probability Distribution Function (PDF) for a Discrete Random Variable

• A discrete probability distribution function has two characteristics:

  1. Each probability is between zero and one, inclusive.
  2. The sum of the probabilities is one.

4.2 Mean or Expected Value and Standard Deviation

• Expected value: Referred to as the long-term average or mean. This means that over the long term of doing an experiment over and over, you would expect this average.

• The Law of Large Numbers: as the number of trials in a probability experiment increases, the difference between the theoretical probability of an event and the relative frequency approaches zero

  

  

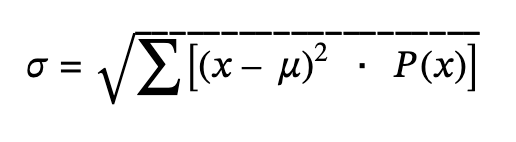
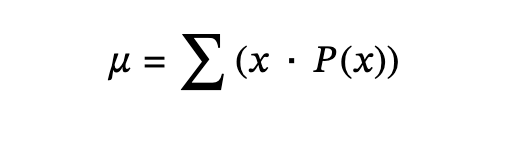
4.3 Binomial Distribution

• 3 Characteristics of a binomial experiment

  • There are a fixed number of trials

  • There are only 2 possible outcomes

  • The n trials are independent and are repeated using identical conditions

    

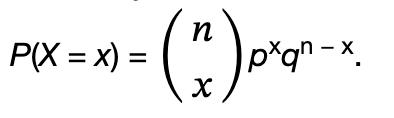
• Binomial probability distribution:

  • Mean→μ = np
  • Variance→σ2 = npq
  • Standard deviation→ σ = √npq.

• Bernoulli Trial: There are only two possible outcomes called “success” and “failure” for each trial. The probability p of a success is the same for any trial (so the probability q = 1 − p of a failure is the same for any trial).

Notation for the Binomial: B = Binomial Probability Distribution Function

• X ~ B(n,p): Read this as "X is a random variable with a binomial distribution." The parameters are n and p; n = a number of trials, and p = probability of success on each trial.
  • Mean→μ = np
  • Standard deviation→σ = √npq

4.4 Geometric Distribution

• 3 Characteristics of a geometric experiment
  • There are one or more Bernoulli trials with all failures except the last one, which is a success. In other words, you keep repeating what you are doing until the first success.
  • In theory, the number of trials could go on forever. There must be at least one trial.
  • The probability, p, of a success and the probability, q, of a failure is the same for each trial. p + q = 1 and q = 1 − p.
• X = the number of independent trials until the first success

Notation for the Geometric: G = Geometric Probability Distribution Function

• X ~ G(p): Read this as "X is a random variable with a geometric distribution." The parameter is p; p = the probability of success for each trial.
  • Mean→μ = 1/p
  • Standard Deviation→σ = √1/𝑝(1/𝑝−1)

4.5 Hypergeometric Distribution

• 5 Characteristics of a hypergeometric experiment
  • You take samples from two groups.
  • You are concerned with a group of interest, called the first group.
  • You sample without replacement from the combined groups.
  • Each pick is not independent, since sampling is without replacement.
  • You are not dealing with Bernoulli Trials.
• X = the number of items from the group of interest.

Notation for the Hypergeometric: H = Hypergeometric Probability Distribution Function

• X ~ H(r, b, n): Read this as "X is a random variable with a hypergeometric distribution." The parameters are r, b, and n; r = the size of the group of interest (first group), b = the size of the second group, and n = the size of the chosen sample.

4.6 Poisson Distribution

• 2 Characteristics of a Poisson experiment
  • Gives the probability of a number of events occurring in a fixed interval of time or space if these events happen with a known average rate and independently of the time since the last event.
  • May be used to approximate the binomial if the probability of success is "small" (such as 0.01) and the number of trials is "large" (such as 1,000).
• X = the number of occurrences in the interval of interest.

Notation for the Poisson: P = Poisson Probability Distribution Function

• X ~ P(μ): Read this as "X is a random variable with a Poisson distribution." The parameter is μ (or λ); μ (or λ) = the mean for the interval of interest. The standard deviation of the Poisson distribution with mean µ is Σ=√μ

Example