Introduction to diffraction and X-ray crystallography

what are spectroscopic techniques?

study the environment of atoms of the molecule we are in, and use this to deduce structural information

Name some spectroscopic techniques

• CD, UV

• FTIR

• NMR

• XAFS

What are scattering techniques?

use scattering to form an image of the molecule → a direct visualisation

Name some scattering techniques

• Dynamic laser light scattering

• SAXS

• Microscopy

• Neutron scattering

• X-ray diffraction

What is structure prediction?

• predicts likey structure from a protein from its sequence using neural networks, rather than experimental data

• useful, not biophysical

• Alphafold2

• Rosettafold

What is the basic idea of NMR?

• Based on some atomic nuclei having a magnetic moment / spin, and the way these spin in the presence of different environment can be used to probe their environments

• Multi-dimensional spectra allow the calculation of distances between nuclei both through space and through bonds

• This allows the calculation of a set of distance constraints that must be obeyed by any molecular structure compatible with the spectra

• This will be repeated many times to generate an ensemble of structures consistent with NMR spectra

  • we get highly conserved regions - always look the same

  • we get regions that vary - all are compatible with experimental observations

  • more dynamic observation

What sort of results does NMR give?

• Structures of small proteins (less than 40kDa)

• Studies of flexible systems (and how well defined domains relate to eachother and moce with respect to eachother)

• Solvent and temperature effects

• Site-specific screening (can observe site specific modifactions / ligands)

  • useful in drug design

What is SAXS?

small angle x-ray scattering

Describe SAXS

• Scattering technique - not used for high resolution structures

• Solution method rather than a non biological environment

• SAXS collects scattered X-rays from molecules in solution.

  • These are assumed to be randomly oriented and so scattered x rays are radially symmetrical around the direct beam

Desrcibe the results of SAXS

• Produces an intensity curve - falls off with resolution

  • but this is not linear

• This volume represents an ensemble of the shapes adopted by the molecule in solution

  • from the images, we can calculate a distribution of pairs of atoms within the structure

    • in the plot, large distribution that are 20A from eachother - this data suggests a rather elongated molecule with a dense region at one end

• Volume calculation is carried out many times and an average calculated – final result could be considered an ensemble of ensembles

• Can be useful with flexible systems

  • can give information about how domains within overall flexible system are in respect to eachother

What does CryoEM use?

Vitrified samples exposed to electrons

What does vitrified mean?

vitrified - flash cooled at liquid nitrogen temperatures (no ice present)

How does CroEM work?

• Vitrified samples exposed to electrons

  • vitrified - flash cooled at liquid nitrogen temperatures (no ice present)

• Images reconstructed using magnetic field as lens

• Technological developments in e-detectors mean Cryo-EM is now an atomic resolution technique for biological samples

  • approaching atomic resolution is routine

  • now the primary method used to determine macromolecular structures

Why is crystallography a good method for structure determination?

• High resolution can be achieved

• can be routinely carried out rapidly if a similar structure has already been solved → implications: if trying to develop drugs or measure small molecule binding against a protein system

• We want to look at objects on the scale of atoms to large molecules → X rays are ideal for this

What is the best thing about crystallography?

Possible to study atomic details of structures from a few atoms up to large macromolecular assemblies → only system that can do this

What can be difficult with crystallography?

difficult to grow good crystals of larger structures → so although they ave been solved by crystallography, we can now use electron microcopy

Why dostructural biology?

Study structure function relationships

• Possible to gain insight into mechanisms of action

• Haemoglobin structure (Perutz) reveals mechanism of oxygen storage

• Ribosome structures (Ramakrishnan, Steitz, Yonath) reveal much about the mechanism of protein synthesis

How can conformations be derived form crystallography and EM?

• Although both crystallography and EM both take static snapshots (rather than recording a dynanic nature of molecule in vivo), taking many snapshots can give information about molecular states

Is the crystalline state used in crystallgraphy an issue?

• Generally no!

• Many enzymes are active in crystalline state (eg. DNA polymerase)

• Crystal structures generally agree well with measurements from spectroscopic techniques (eg. NMR, fourier transform IR, fluorescence)

  • rare to significantly diverge from solution based methods

  • generally - the crystalline state doesnt introduce large artefacts

Describe how protein packing in crystals doesnt actually affect structure

• Proteins are often observed in more than one “packing” in different crystal forms: generally the differences are either slight (~0.1 Å), or important (e.g. multiple conformational states)

  • usually - the structure is the same

  • we see 2 well defined different states - useful

• Protein crystals are typically > 30% solvent, and less than 30% of a protein surface is involved in crystal contacts

  • in crystals, average 50% solvent, so most of the surface are interacting with water

  • theres only a few points of the protein making contacts

What sort of concentration are protein crystals?

very high concentration solutions (typically ~10 mM)

What are the main processes in crystallography?

• Expression/purification

• Crystallisation → need to grow crystals

• Data collection → by exposing toX-rays

• Map calculation → exposing to electron density maps

• Map interpretation → interpreting the electron density map

What do we need too form a crystal and why?

Need a saturated solution (and super saturate it) → so the salt comes out of solution, slowly

Why can’t we use heating and cooling for protein crystallisation?

proteins will denature and wont form a crystal

What is the main method of protein crystallisation>

Vapor diffusion - this allows the concentration of protein in a drop to gradually increase

What are the different methods of vapour diffusion>

hanging or sitting drops, drop of solution under oil (gradual evaporation of water through the oil layer), small scale batch dialysis

What are the variables that can vary our ability to crystallise?

• Temperature

• pH

• Precipitant - choice of and concentration

  • adding different chemicals that alter protein solubility as concentration changes

• protein concentration

• Salt

• Detergent

• Ligands

  • may bind the protein and facilitate crystallisation - eg. aid contact formation

→ many variables, difficult to screen systematically, most large groups rely on automation and brute force

What is on the X and Y axis for the solubility phase diagram?

Y axis = conc of protien of interest X axis = crystallant concentration (we hope this will reduce the solubility - historically a salt (Ammonium sulfate), now - polyethylene glycol

Describe the 3 main defined zones of a crystal phase diagram

• clear protein solution → single phase, protein is soluble. solubility line is the boundary of this stable soluble state

• metastable soluiton → possible for the protein to separate into soluble protein (saturated solution) and some that has come out of solution.

  • how this behaves depends on other conditions

  • will have a boundary - on one side there is a possibility of spontaneous nucleation (crystallisation) and a groeth zoen (can still come out of solution but dont crystallise)

• precipitate plus protein two phase

what occurs to proteins in the clear protein solution stage?

single phase, protein is soluble. solubility line is the boundary of this stable soluble state

what occurs to proteins in the metastable solution stage?

• possible for the protein to separate into soluble protein (saturated solution) and some that has come out of solution.

  • how this behaves depends on other conditions

  • will have a boundary - on one side there is a possibility of spontaneous nucleation (crystallisation) and a growth zone (can still come out of solution but dont crystallise)

what occurs to proteins in the two phase stage?

protein aggregates and comes out of solution

Describe the process of crystallisation in vapour diffusion

• Put drop of protein on coverslip

• Add a drop of crystallant solution - both are at half their original concentration

• Fix this on a resevoir above a solution

• Vapor pressure in the sealed environment is dominated by the reservoir

  • osmotic effects mean that concentration in the droplet are driven to equilibrate wit the concentration in the reservoir

  • water leaves until the concentration of crystallant is equal to that in the reservoir

  • leads to equilibration

    • should take us into the spontaneous nucleation zone, and so we get crystals grow

    • protein concentration drops because coming out of solution

What can go wrong in crystallisation?

• Over nucleation

• Spontaneous precipitation

• Non-crystalline phase separation

• Failure to reach super saturation

What is over nucleation?

can get too many nuclei and not have enough protein left to form individual crystals

What is spontaneous precipitation?

everything aggregated out - need a new condition

What is non-crystalline case separation?

• protein has come out of solution but not nucleated

• sign you are approaching a useful condition, need to stimulate nucleation

What is failure to reach super saturation?

• protein is so soluble, and so it stays in solution

• can usually find a way to drive it to precipitation

What is the basics of forming a crystal?

copies of a simple component (the unit cell) are packed together by translation to fill space.

• This packing must be infinitely extensible in all directions

  • no sudden boundaries

What is a plane lattice?

• A plane lattice is an infinitely extensible construct of intersecting parallel and equidistant lines, forming identical unit lattices.

  • have an origin, a square unit lattice defined by vectors a and b (have magnitude and direction, defining their direction of movement from the orign. → these have an angle between them (gamma) a = b, and gamma = 90

  • this describes the square lattice too

What is a unit cell?

what is repeated to make a crystal

What does a unit cell consist of?

• nit lattice - described by vectors

• Motif - the actual content of the unit lattice

Describe how origins can be different in different crystals

As long as each unit cell contains the same integer number of molecules, this is fine - doesnt have to be one in one - could be spread ver multiple

Describe what a symmetry operation must do in a crystal

• Applying a symmetry operation to cannot generate any changes in a motif

  • the protein has to stay the same

  • for chiral molecules such as proteins, this rules out any inversions or mirror operations → we cant have any mirror images

What are the different symmetry operations in the unit cell?

• Translational symmetry

• Rotational symmetry

Describe rotational symmetry

• Axis of rotation - A rotation can only involve operations by (360/n)° → in between each copies, you wont see any partial copies

• ll symmetry operations must also be compatible with the translational requirements of a given lattice

  • as a consequence, only 2-, 3-, 4- and 6-fold rotations are allowed and are indicated in the International Tables for Crystallography by dyad, triad, tetrad and hexad symbols

• Rotational symmetry must be compatible with lattice symmetry. eg. a square plane lattice is not compatible with a 3-fold rotation

Describe the 3D symmetry of crystals

molecule in a unit cell is packed together in space, and these form a crystal

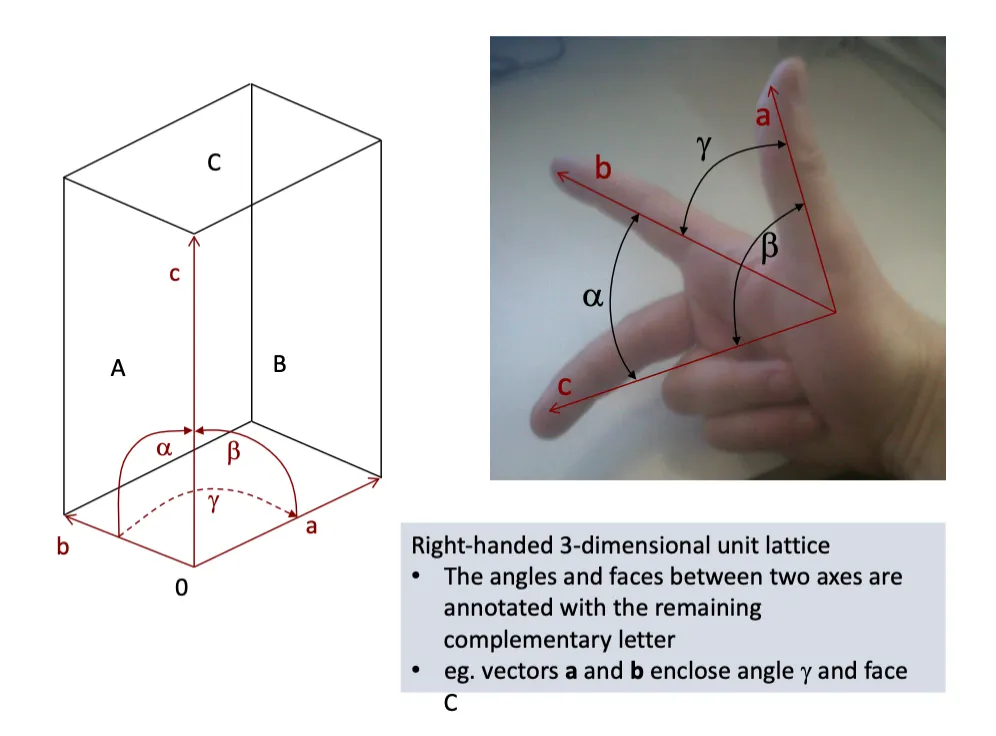
What is a right handed unit lattice?

• right handed , 3D lattice

• Can use the right hand to show the relationship between a b and c

• Whatever the missing letter is is the angle between the two

What is a primitive lattice?

one lattice point per unit cell

What is a lattice point?

Lattice points are all connected to other unit cells through translation

What are the symmetry contrasts of a primitive lattice?

If a lattice shows 4 fold rotational symmetry, all unit cell angles must be 90º → consisitent with tetragonal or cubic systems

• Restricts the possible symmetry elements

What is a centred lattice?

contain two or more lattice points per cell

When is a cantered lattice possible?

• Possible when unit cells interleave with eachother

  • this means each unit cell contains additional lattice points

  • so there are regions of the unit cell that are obliged to be symmetrical to eachother even thouhg there is no rotation

    • higher symmetry since for a centred cell to exist, some regions of it must be identical to corresponding (but not spatially identical) regions of adjacent cells.

What is a C centred lattice?

Centered in the C face

What is an F centred lattice?

Centeref in all faces

What is an I entered lattice?

A body entered lattice at the centre of the unit cell

What are screw axis (roto-translation)

• Combines rotation and translation along the axis

  • produces a helical arrangement in the crystal

• Forming a helix passing through a crystal

• In two fold symmetry - If we move both 180º and moe up half the height of the unit cell, we have arrived at the same poistion in the next unit cell → so we form a helix

What are the general bits about symmetry?

• 65 possible space groups for proteins - 230 if things can be non-chiral

• Large scale of combinations

• Main thing: unit cells repeat translationally, within the unit cell, all othe symmetry is assymetruic units related to eachother by symmetry

• Symmetry in the crystal lattice is paralleled by symmetry in the diffraction pattern

What are Xray sources?

Synchrotron sources

When are synchrotron radiation emiited

• Synchrotron radiation is emitted by charged particles travelling at relativistic speeds when they accelerate.

• In a synchrotron this involves electrons being steered around a curved path by magnetic fields.

  • accelerate towards the centre of a circle, and as a result it emits radiation

• Synchrotron radiation is generated whenever the electron beam changes direction.

What can synchrotrons emit?

Broad, continuous spectrum from microwaves to hard X-rays is produced.

Describe the elements of a synchrotron storage ring

• Bending magnets - cause the electron beam to bend → we can also make it bend multiple times as it moves past different pairs of magnets - undulators

  • If the electron beam is passed through an array of magnets with alternating polarity, SR is generated at each bend in the e-path.

  • bend particles round corners to close the orbit and give rise to SR

  • Electrons pass through these magnets and are deflected from their straight path by several degrees. This change in direction causes them to emit synchrotron radiation

• Focusing magnetic structures

  • quadrupoles, sextupoles, no SR

• Periodic magnetic structures

  • wigglers, undulators

What is the function of a goniometer>

device for precisely fixing a sample - can rotate it and transalte it

What are the traditional X ray detectors? What are the issues

• photographic film

  • issues: slow, labour intensive, low dynamic range

What are the newer X ray detectors?

CCDs and pixel counting detectors

What is good about CCDs?

• charge coupled devide

  • fast, low noise, high dynamic range

What is good about pixel counting detectors?

• new technology, each pixel counts photon events independently

  • so fast they have changed the nature of data collection

    • constant roation, no more stopping for detector readout

  • very high dynamic range

Describe how data is collected in diffraction (basic_

• We have a crystal that we rotate - this is because we can only sample a small fraction of spots in a given orientation

• Set crystal to detector distance (resolution)

• Centre crystal in beam set crystal to detector distance

• Test diffration quality at 0, 90º

• Determine data collection strategy

• Set up data collection

• Collect data

What is grid scanning?

crystal mount is translated and short exposures are taken of many areas of the sample.

How do we form an image in diffraction techniques, what is the difference with X-rays?

• An image is formed by

  • exposing sample to radiation

  • radiation is scattered

  • a lens (in EM) recombines these scattered waves

  • the final image depends on all of the diffracted rays

• For X-ray, there is no lens, and so wave recombination is done computaitonally

What radiation do we consider in diffraction?

We only consider elastically scattered radiation → photons that do not lose any energy

What are the requirements for diffractive techniques?

• Must use radiation with wavelength approximately the size of details to be observed (atomic bonds are approx. 1.5Å in length) therefore electrons, X-rays or neutrons

• Only “elastically scattered” radiation considered – we ignore the contribution of photons that lose some energy to the scattering object

• Combination achieved either by focusing (EM, optical microscopy) or computationally (X-ray or neutron diffraction)

• Each pixel of the reconstructed image depends on all of the diffracted waves

What is a Fourier syntehsis?

representation of a complex function in terms of a set of sine waves

Describe the main point of a Fourier synthesis

• solving a structure by X ray crystallography is a process of adding waves together

  • we need some way to treat and consider waves

  • way of representing a periodic function (electron density in a crystal) as a set of sine waves

Why is a Fourier synthesis useful - why does it work?

• adding waves with different frequencies, amplitudes and phases allows for a good approximation of atomic distribution

• The fourier transform of the unit cell gives a set of peaks, ith the large peaks corresponding to the most important frequencies

• These correspond exactly to the sine-wave frequencies used to reconstruct the unit cell. The peak height also corresponds to the sine-wave amplitudes

What information do we lose / gain when we do a Fourier transform?

we lose information amount the phase of the waves, but gain information about frequency and amplitude

What gives rise to the position of diffracted spots in X-ray crystallography?

Size and shape of the unit cell

What gives rise to the intensity and phase of the diffraction pattern in crystallography?

The molecules structure

Explain why atoms scatter X rays

• Dealing with an electromagnetic wave and its interaction with charged species (electrons mostly)

• This makes it oscillate, and these acts as new sources

• When multiple electrons are emitting, scattered waves interfere with eachother, producing a non cylindrical symmetric pattern

  • Where there is more than one such piece of charge, the intensity of the scattered beam is prone to interference.

• Scattered intensity in any direction depends on the entire charge distrubution

• Each point in the reconstructed image depends on all recorded diffraction

When do waves scatter in phase?

• When the path length is the same for a given 2 waves

  • leads to positive interference between the two waves

• When the path lengths differ by nλ

  • integer multiple of the wavelength of the radiation

  • this is braggs law λ=2dsin0

  • not reflecting - x rays are passing through the crystal and being scattered at a specific angle (theta), and so we see positive interference

How are lattice planes defined?

defined by how they intersect the unit cell axes

What are the different miller indices to describe planes?

• h - how many times a plane crosses the a axis

• k - how many times a plane crosses the b axis

• l - how many times a plane crosses the c axis

  • must be integers - only this satisfies the constructive interference conditions

What do larger miller indices mean?

• more times the planes cross the axis of the unit cell, finer set of resolutions

  • planes are closer together

  • smaller d spacing

  • higher scattering

  • higher resolution

What is a reciprocal lattice?

considering the family of diffracted reflections from a crystal

Why can we consider the reciprocal lattice as so?

There are sets of planes that only diffract if they cut each of the cell edges in in integral number of times

• this is because these are the only ones that give rise to constructive interference

• We can therefore imagine a conceptual grid of reflections related to the geometry of the repeating unit cell of the crystal.

  • reciprocal lattice - considering the family of diffracted reflections from a crystal

What dies a larger unit cell mean for real space and reciprocal lattice points

• Larger the unit cell - the smaller the difference between bragg angles for neighbouring sets of planes in a lattice and the smaller the spacing between reciprocal lattice points

  • large unit cell results in a small separation in reciprocal space

What does each property mean on an argand diagram?

• Waves to add together can be characterised by amplitude and phase

• Waves as a vector

  • amplitude = magnitude

  • phase = angle of rotation around a complex plane

How do we add up waves in an argand diagram?

We can represent waves as vectors, and add them by drawing them nose to tail

How does addition of atomic scattering vectors produce a structure factor?

• Each atom contributes a scattering vector upon interaction with X rays

• The phase depends on the atoms pposition relative to lattice planes

• The structure factor is the sum of all atomic contributions

  • and so is dependent on the arrangement of atoms in the unit celll

• To work out the contribution of all of the waves, we draw a vector from the start of the first to the end of the last

  • this is a structure factor - dependent on the arrangement or structure of atoms in the unit cell

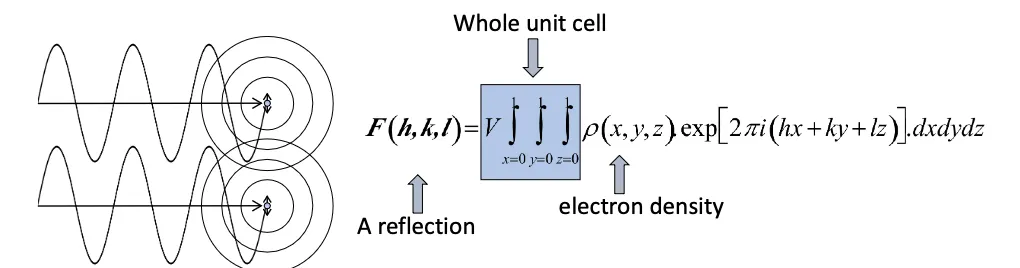
What is a structure factor?

a mathematical function describing the amplitude and phase of a wave diffracted from crystal lattice planes characterized by Miller indices h,k,l.

WHat is the structure factor equation?

What do we aim to get from structure factors?

• 
  we need to calculate electron density from structure factors

What are the principle begins the electron density eqution?

• Real space function

• A lens will bend the scattered light, applying a wave shift and reforming an image

• Structure factors are in reciprocal space

• Electron density - the electron density at a point in real space

• The electron desnsity is obtained by the inverse fourier transform

• Each point on the map is a sum of may waves with different phases and amplitudes

• Normally a lens will

  • Bend the scattered light pattern

  • Apply a phase shift

• Each “pixel” of the image formed is therefore a sum of many scattered waves. These will add up in a way that depends upon their phase and on the position of the pixel.

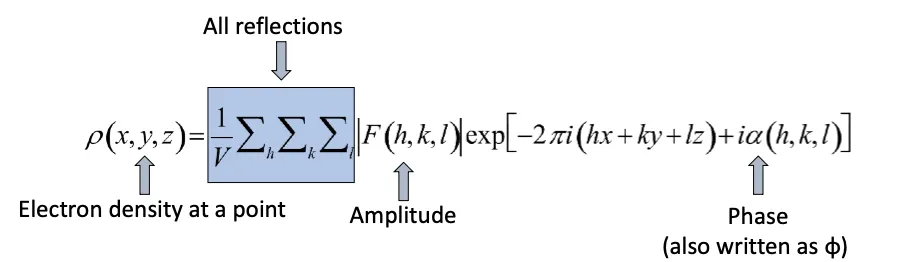
What are the components of the electron density equation?

• contains terms for the amplitde with a set of miller indicis and the phase

• has a phase term, amplitude term and electron density is in real space

What does a lens do?

• Bend the scattered light pattern

• Apply a phase shift

What is the electron density equation?

What is convolution?

take advantage of the understanding of the waves as Fourier phenomena

What are the two theories of convolution?

• Convolution theorem

• Inversion theorem

What is the convolution theorem?

• Convolution of two functions mixes them together. For functions f and g this can be expressed by the formula:

  • If f is the motif (protein of interest) and g is a lattice (crystal lattice), both are described as funcitons

  • The convolution of these two is f*g - there is a copy of the molecule at every point in the lattice

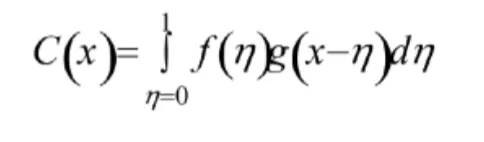
What is the basic explanation of the convolution theorem?

The convolution theorem states that the Fourier transform of the convolution of two functions is equal to the product of the Fourier transforms of the two separate functions