Physics Final Review: Magnetic Fields and Forces

These flashcards cover key concepts and definitions about magnetic fields, forces, electromagnetic induction, and other related topics in physics, aimed at aiding in exam preparation.

Magnetic Poles

Like poles repel each other, while opposite poles attract; magnetic poles always come in pairs.

Magnetic Field (B)

The magnetic field is measured in Teslas (T) and represents the magnetic force experienced by a charge.

Magnetic Flux (\phi )

The quantity of magnetic field passing through a surface, calculated as \phi=B*A*cos(\theta).

Lorentz Force

The force on a charged particle moving through electric and magnetic fields, represented asF=q(E+v\cdot B).

Cyclotron Radius (R)

The radius of the circular path of a charged particle moving perpendicular to a magnetic field, given by R = (mv) / (|q|B).

Torque on a Current Loop

Torque experienced by a current-carrying loop in a magnetic field, given by \tau=NIABsin(\theta)

Right Hand Rule (RHR) #1

A method to determine the direction of magnetic force (and current) on a moving positive charge: point the fingers in velocity direction, curl towards magnetic field, and the thumb indicates force direction.

Faraday’s Law of Induction

Indicates that an EMF is induced in a circuit when the magnetic flux changes, described by the formula EMF = - N * (change in Flux / change in time).

Lenz’s Law

States that the direction of induced current will oppose the change in magnetic flux that produced it.

Motional EMF

Induced electromotive force when a conductor moves through a magnetic field, represented by EMF = B * L * v.

Electromagnetic Waves

Transverse waves formed by oscillating electric and magnetic fields perpendicular to each other, propagating in the direction of the wave.

Snell’s Law

Describes the relationship between the angles of incidence and refraction when light passes between two different mediums, given by n1sin\left(\theta_1\right)=n2sin(\theta_2).

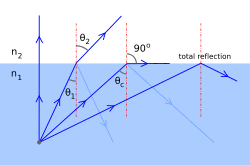
Total Internal Reflection

Phenomenon that occurs when light travels from a medium with a higher refractive index to one with a lower refractive index, at an angle greater than the critical angle.

Constructive Interference

Occurs when waves meet in phase, leading to an increase in amplitude.

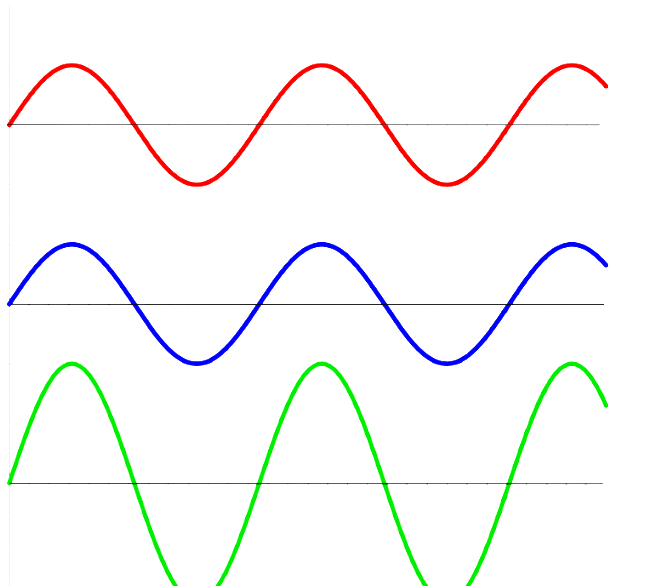
Destructive Interference

Occurs when waves meet out of phase, leading to a reduction in amplitude.

Diffraction Grating

An optical component with a regular pattern that splits and diffracts light into several beams traveling in different directions.

Magnetic Force Direction (Negative Charge)

For a negative charge, the magnetic force is in the opposite direction to the thumb's indication when using RHR #1 for positive charges.

Angular Speed of Charged Particle (Cyclotron Motion)

The angular speed of a charged particle moving perpendicular to a magnetic field is given by \omega = (|q|B) / m.

Velocity Selector Principle

A velocity selector uses perpendicular electric (E) and magnetic (B) fields to filter particles of a specific speed v = E / B.

Magnetic Force on a Current-Carrying Wire

The magnetic force on a straight current-carrying wire in a magnetic field is F = I(L \times B), with magnitude F = ILB \sin(\theta). The net magnetic force on a closed current loop in a uniform field is zero.

Magnetic Dipole Moment (\mu)

A vector quantity (\mu = NIA) describing the magnetic strength of a coil/loop, where N is turns, I is current, and A is area. It determines the torque: \tau = \mu \times B.

Right Hand Rule (RHR) #2 (Dipole Moment/Area)

To determine the direction of the Area Vector (A) and Magnetic Dipole Moment (\mu) for a current loop: Curl fingers in the direction of the current, and the thumb points in the direction of A and \mu.

Magnetic Field of a Long Straight Wire (Properties)

Field lines form circles around the wire. Its direction is given by RHR #2 (thumb = current, fingers = B-field). The magnitude of the field decreases as distance from the wire (r) increases.

Force Between Parallel Current-Carrying Wires

Two parallel wires carrying current exert force on each other: currents in the same direction attract, while currents in opposite directions repel.

Magnetic Field at Center of Circular Loop

The magnetic field at the center of a circular current loop with N turns is given by B = N(\mu0 I) / (2R), where R is the radius and \mu0 is the permeability of free space.

Magnetic Field of a Solenoid

Inside a solenoid (a long bent coil), the magnetic field is uniform and given by B = \mu_0 n I, where n is the number of turns per unit length (N/L) and I is the current.

EMF in AC Generator

An AC generator converts mechanical energy into electrical energy by rotating a coil in a magnetic field, producing a sinusoidal induced EMF using slip rings.

Electromagnetic Wave Field Relation

In an electromagnetic wave, the magnitudes of the electric (E) and magnetic (B) fields are related by E = cB. The wave propagates in the direction of the vector cross product E \times B.

Brewster’s Law for Polarization by Reflection

Brewster’s Law states that reflected light is fully polarized when incident at the Brewster angle (\thetaB), given by \tan(\thetaB) = n2 / n1, where n1 and n2 are the refractive indices of the two media.

Law of Malus

The Law of Malus describes the intensity (I) of polarized light after passing through an analyzer: I = I0 \cos^2(\theta). If the initial light is unpolarized, its intensity is reduced to I0 / 2 after passing through a first polarizer.

Law of Reflection

The Law of Reflection states that the angle of incidence is equal to the angle of reflection.

Index of Refraction Definition

The index of refraction (n) is defined as the ratio of the speed of light in vacuum (c) to its speed in a given medium (v): n = c/v.

Spherical Mirrors (Concave vs. Convex)

Concave (converging) mirrors have a positive focal length (f) and can form real or virtual images. Convex (diverging) mirrors have a negative f and always form virtual, upright, and smaller images. For spherical mirrors, f = R/2.

Thin Lens/Mirror Equation

The Thin Lens/Mirror Equation is a fundamental relationship: 1/p + 1/q = 1/f, where p is the object distance, q is the image distance, and f is the focal length.

Magnification Formula

Magnification (M) in optics is the ratio of image height (h') to object height (h): M = h'/h. It is also given by M = -q/p. A negative value for M indicates an inverted image.

Conditions for Light Interference

Two essential conditions for observable light interference are that the light sources must be coherent (maintain a constant phase difference) and monochromatic (emit a single wavelength).

Young’s Double Slit (Constructive Interference)

In Young's double-slit experiment, constructive interference (bright fringes) occurs when the path difference is \delta = d \sin(\theta) = m \lambda, where m = 0, 1, 2, …

Single Slit Diffraction (Minima Condition)

For single-slit diffraction, minima (dark fringes) occur when a \sin(\theta) = m \lambda, where a is the slit width and m = 1, 2, 3, … (excluding m=0).

Bragg's Law for X-Ray Diffraction

Bragg's Law describes constructive interference for X-rays diffracted by crystal planes: 2d \sin(\theta) = m \lambda, where d is the atomic spacing and m is the order number.

Plane Mirror

Forms a virtual, upright, and same-size image. The image distance (q) is equal in magnitude and opposite in sign to the object distance (p), i.e., q = -p.

Converging Lenses (Convex)

Lenses that are thicker in the middle, have a positive focal length (f), and converge parallel light rays to a focal point. They can form both real and virtual images.

Diverging Lenses (Concave)

Lenses that are thinner in the middle, have a negative focal length (f), and cause parallel light rays to spread out as if from a virtual focal point. They always form virtual, upright, and smaller images.

Concave Mirror

Also known as a converging mirror, it possesses a positive focal length (f = R/2). It forms real, inverted images when the object is placed beyond its focal point (F), and virtual, upright, and magnified images when the object is between F and the mirror surface.

Convex Mirror

Also known as a diverging mirror, it has a negative focal length (f = R/2). It consistently forms virtual, upright, and diminished (smaller) images for any object position. They are commonly employed as security mirrors and rearview mirrors in vehicles due to their wide field of view.

Double Convex Lens

A type of converging lens where both surfaces are convex. It features a positive focal length (f) and can form both real, inverted images (object beyond F) and virtual, upright, magnified images (object within F). Used in applications such as magnifying glasses and camera lenses.

Double Concave Lens

A type of diverging lens where both surfaces are concave. It is characterized by a negative focal length (f) and invariably produces virtual, upright, and diminished (smaller) images, regardless of the object's position. Used in applications like correcting nearsightedness.