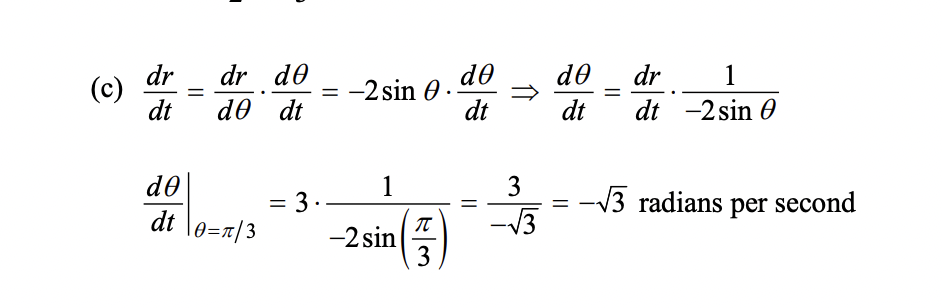Calculus BC (more like BS)

total distance vs distance vs distance

total distance = ∫√(dx/dt² + dy/dt²) dt

distance = √(y-distance)² + (x-distance)²

distance = ∫ v(t) dt

Disk

washer

shell

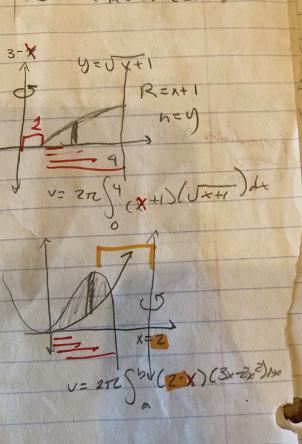
v = π∫ba (f(x)² dx

π∫(top - AOR)² - (bottom - AOR)² dx

v = 2π∫ height (x)

• For shell, x is x - the distance from revolution axis ex. | _ _ x would be (x-2)

Disk/washer = perpendicular rectangle

Shell = parallel rectangle

x and y for polar curves

slope for polar curve

area

x = rcosθ

y = rsinθ

y/x = tanθ

• y/x is slope

1/2∫ f(θ)² dθ

• between curves = ½ ∫(R²-r²) dθ

eulers method

y = y current + deltax( dy/dx)

e^x maclaurin

e^x = Σ x^n / n! = 1 + x + x² / 2! + x³ / 3! + …

sin(x) maclaurin

Σ (-1)^n x^(2n+1) / (2n+1)!

= x - x³ /3! + x^5/5!

cos(x) maclaurin

Σ (-1)^n x^(2n) / (2n)!

= 1 + x²/2! + x^4/4! -

ln (1+x) maclaurin

Σ (-1)^(n+1) x^n / n

= x - x²/2 + x³/3

convergence at -1 < x < 1

1/(1-x) maclaurin

Σx^n = 1+ x + x² + x³ . . .

convergence at |x|<1

what to do when given a maclurin where you need to substitute

u = lsdfkjsdlkf

and substitute like you would with intergration

Errors legrange and alternating series

boundaries of how big the error wil be

• the error is always smaller than the next term

Alternating serires: error is less than the next term after the one. you are “summed”

• bn HAS TO BE decreasing, negative, and lim n—>∞ = 0

check if you’re using the right formula

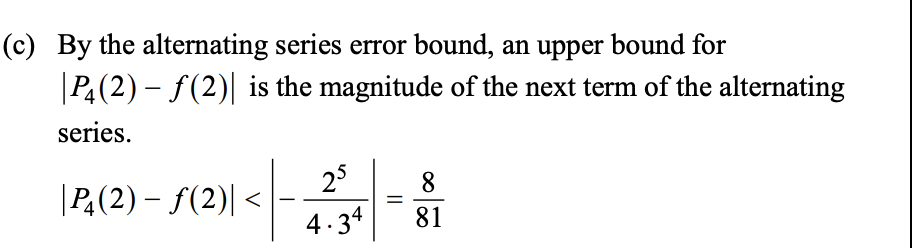
Rose curves

n petals when n is odd

2n petals when n is even

• t = a cos (nø) —> reflectable against x axis

• t = a sin (nø) —> reflectable against y-axis

petals are as long as “a”

leminscute

a rose curve basically but only 2

r² = a²sin(2ø)

• if a² it /

• if a² it is \

r² = a²cos(2ø)

• if a² it’s —-

• if -a² |

a is how long each curve is

circles

r=acosø

• if a is pos, directed right

• if a is neg, directed left

r=asinø

• if a is pos, goes up

• if a is neg, goes down

a is the diameterli

limacon

r = a+- bsinθ

• if b is pos, opens up, if b is neg opens down

r = a +- b cos

• if b is pos, opens right, if b is neg opens left

**opens means where the majority of the mass is

When a/b <1 —> has an inner loop that’s b-a long

• each “bump” is a long, length is a + b (NOT INCLUDING THE BUMP)

When a/b = 1 —> cardiod (the heartshaped one)

• each “bump” is a long, length is a + b (NOT INCLUDING THE BUMP)

• no inner loop

When 1 < a/b < 2 —> dimpled limison (kind of heart shaped but doesnt curve in as much

• each “bump” is a long, length is a + b (NOT INCLUDING THE BUMP)

• no inner loop

When a/b > 2 —> dimpled limison

• no inner loop

• each “bump” is a long, length is a + b (NOT INCLUDING THE BUMP)

• basically a circle with a flat edge

First thing you check (no actual solve)

Divergence test

if lim n→∞ ≠ 0, than it diverges

if it does = 0, than inconclusive

Obvious ratio in format a(ratio) ^n-1

actual solve

geometric series

∑ ar^(n-1)

• if |r| < 1 than converges to a/(1-r) **a is the first term, r is the common ratio that you get by dividing any an+1/an

  • if |r| ≥ 1, than diverges

quick converge or diverge when you see 1/n^p or or (1/n)^p

p-series test

1/n^p

• if p>1, converges

• if p ≤ 1, diverges

looks like something we know

• no facorials but like 1/(n²+1)

comparison test

a(n)<b(n)

• if the bigger converges, the smaller converges

• if smaller diverges, bigger diverges

1/(nln(n)) diverges

looks like something we know but a bit more confusing

limit comparison test

lim n→∞ (small/big) = C

• if c is finite positive number: both an and bn converge OR both diverge

alternating / conditional convergence

if an is convergent and |an| is convergent, it’s called absolute convergence

• if it’s not convergent when you’re doing |an|, it’s not absolutely convergent

if alternating series

Alternating series test

if it’s alternating, lim n→∞ = 0, decreasing

• converges

(messy stuff) ^n

lim n→ ∞ n√a(n)

Root Test

• if L<1 then absolute convergence

• if L>1 or = ∞ than diverges

• if L=1 than use another test

if it looks intergratable

intergral test

• conditional: positive, continuous, and decreasing

if intergral converges, than the an converges

if intergral diverges, than an diverges

factorials

ratio test - remember it’s absolute value

L = lim n—>∞ |an+1/ an|

• if L< 1 converges absolutely

• if L>1 diverges

• if L=1 use a diff test

can’t just take out factorials though like

(n+2)!/(n+1)! = n+2

also can’t just take out constants that loo like they’re with the n

• ex. usually just auto take out everything except for the -1 and x, but in this case there was a 3^1

  

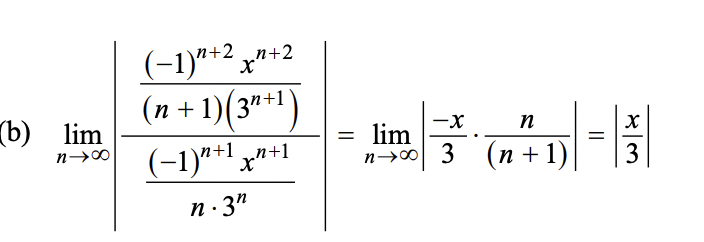
reimans sum using ∫an and Σ

figure out what the common theme is and what the ∆x is because reimans sum is ∆x * f(∆x)

• then you’d plug in only f(x) into an intergral and use ∆x to find the boundaries (a and b)

intergral of convergence

remember when the x is based around something you alater the intergral of convergence

• check for brackets or parenthesis

this doesn’t only apply to ratio test

• ex. an(x-3)^n is convergent at x=5, this means we know interval of convergence is AT LEAST 1<x<5 HOWEVER we don’t know for sure the other interval that we guessed (in this case x=1) is FOR SURE convergent ALWAYS TESTTT

arc length

S = ∫ √( 1+(f’x)² ) dx

• typically you’d have to combine the 1+(f’x)² into one fraction and then take out the denominator bcs it has an exponent

applying L’hopitals to limits

• must prove l’hoptials exists first

• ln both sides and switch the ln&limit

• make the fraction a denominator, and apply l’hoptials until you can simplify it down to lny=constant

  • y = e^constant

Compounding continuously

A = Ce^(rt)

compounding noncontinuously based on year

A = C(1+r/n)^(nt)

• C = initial deposit

  • n is based on the time unit, ex if it’s year n=1, if it’s month n=12

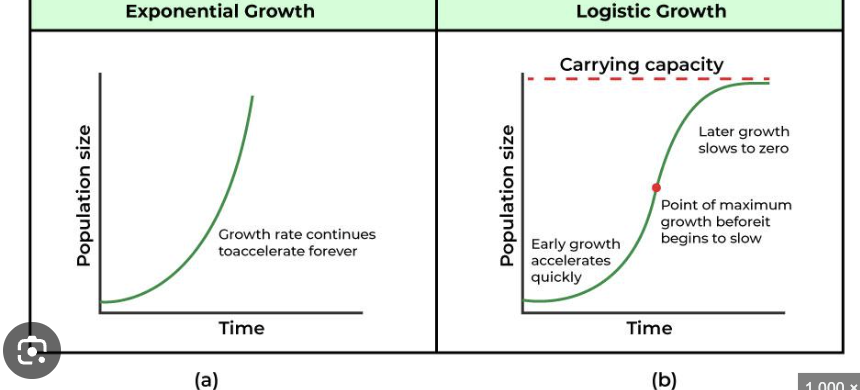
Logistical Growth Equation

dy/dx = Ky(1-y/L)

y = L(1+be^(-Kt)

• L is largest value (carrying capacity)

• K is the constant of perpetuality ( K is pos/neg depending if function is increasing/decreasing)

• b (find what this is using y(0) )

Halfway is the fastest growing point

i think both graphs look the same (for dy/dx and y)

LIATE

uv - ∫vdu

Use the table to see if you need to keep on going

• don’t forget the +C or the boundaries

seperation of variables

put the +C on the x side, solve for the C RIGHT AFTER intergrating

• when 1/(4-y) remember u = 4-y, du = -dy YOU NEED TO ADD THE - SIGN

slope fields

0 slope is ←→

undefined slope is | d

∫a^u du

derivative of a^u

a^u / lna + C

ln(a)a^u

∫du/√(a² -u²)

arcsin u/a +C

∫du/u√(a² -u²)

1/a arc sec |u|/a+C

∫du/ (a² + u²)

1/a arctan u/a +C

∫tan u

-ln |cosu| +Cf

∫sec u

ln |sec u + tan u|

∫cot u

ln |sinu|+C

∫cscu

-ln|cscu + cotu| +C

∫1/(1+e^x)

∫1+e^x / 1+ e^x - e^x / 1+e^x

• bcs 1 + e^x - e^x = 1

sin² x

1 -cos2x / 2

cos²x

1+cos2x / 2

trig substituition

1. substitute the “x” into the √

2. plug in the du as well

3. after intergrating find ø using triangle

√(a²-x²)

• x = a sin ø

√(a²+x²)

• x = a tanø

√(x²-a²)

• x = a secø

if n is even ∫π/2 cos^n (x) dx

if n is odd ∫π/2 0 cos^n (x) dx

• remmember cos and sin are interchangeable here

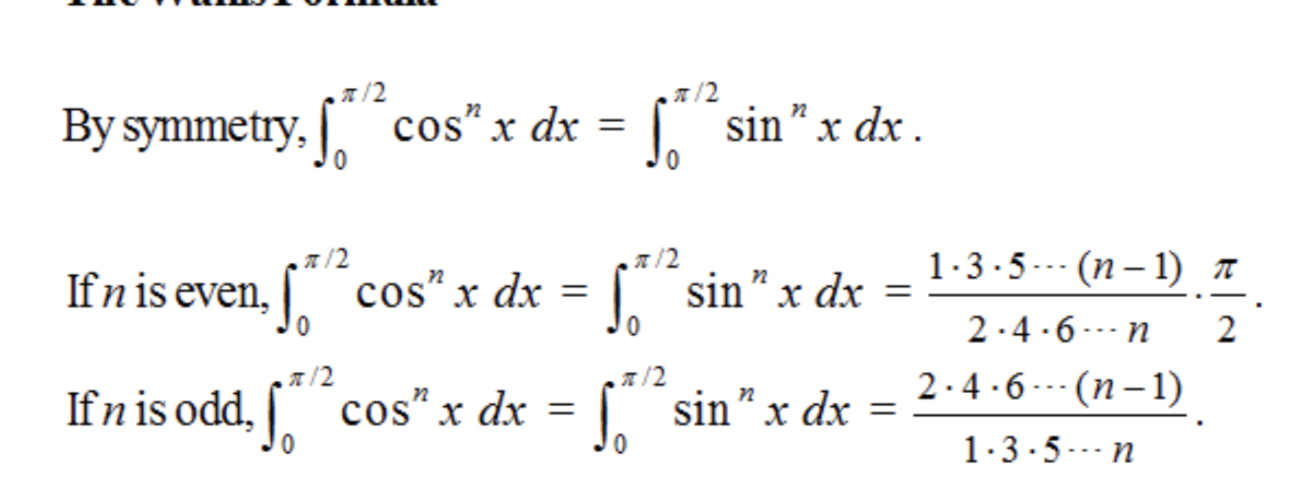
odd : (2/3) (4/5) (n-1)/n)

even : (π/2) (1/2) (3/4) (n-1)/n)

infinity intergrals

split into ∫∞ o and ∫o -∞

AND

lim b—>∞ ∫b a

inconsistencies intergrals

you have to split it to where the inconsistency is

ex. ∫2 -2 (1/x)

= ∫2 0 (1/x) + ∫0 -2 (1/x)

MVT

continuous differentialble

if point c in an open interval f’c equals average rate of change

trapezoidal rule

(b-a)/2n [f(x0) + 2 (fx1) + . . . f(xn)]

b-a is ∆x

• only works if they’re all the same ∆x

More standard ver: (a+b / 2) (n)

limn→∞ sigma [F(b-1)i/n ] (b-a / n)

Σ c= cn

Σ i = n(n+1)/2

Σ i² = n(n+1)(2n+1)/6

Σ i³ = n² (n+1)² /4

1. replace x with the ∆x/n **remember that the one inside f(x) has an i as well

2. take out the ∆x /n on the outside of the limit because it’s just a constant

3. Seperate sigma notation until i is isolated into one of the formulas above and the constants are isolated (there should be no n’s as of now INSIDE the sigma notation)

4. no more sigma notation, simplify n until you can use a/b rule to find what the area is equal to (remember to multiply the earlier ∆x/n back in)

when a/b have the same exponents that’s what A is equal to

Area of Surface Area

2π∫ y * (√1+(y’(x))²) dx

horizontal asymptote

num<den y = 0

num = den a/n coefficients

num > den no asymptotes

slant asymptote

an +1 / an

• divide using long division, and ignore whatever the remainder is, what you calculated is the asymptote

to find vertical column of water with cross section of 3

∫3*density

• boundaries are the heights

two critcal points means what

no where does f’(x) = 0

1/ln(n+1) and 1/n

1/ ln(n+1) > 1/nsl

distance formula

for f(x) when it’s less than what’s given f’x

f(d) = ∫g(x) from b —> a

f(d) = f(b) - f(a)

-f(a) = f(b) - f(d)

f(a)= F(d) - F(b)

average value formula

1/b-a ∫f(x) dx

whenever it says absolute maximum or minimum

use the end points as well no matter what

whenever you get a limit with absolute value

use the left/right limit, not l’hopitals

which grow faster logarithms or polynomials

polynomials

• logarithms growth is significantly slower compared to polynomials.

how would you go about solving this

find the f’(x) macluarin first and then intergrate each individual term, just like how’d you do if it was asking for the derivative

d) because it’d change too many times

average value vs rate

∫ vs f(x) -f(x) / x2-x1

when there’s a line of sorts what to pay attention to when it’s asking for the max/min

when it starts (not always at t=0)

evt check for all of the endpoints+crits

IVT

continuous

if f(a)<k<f(b) there’s somewhere with f(p)=k

volume derivative questions

don’t plug in everything until you’re done deriving, especially if you can’t replace one variable with another (ex. h≠2r)

if one of the errors doesn’t tell you the term number

see what the f(x) equals too and then that’s what term it is

ex. |f(1/2) = 4|

• Look for which term when you plug in ½ equals 4

  • Use the term after

if there’s a simple fraction and you NEED to find convergence

geometric series USE AS OFTEN AS YOU CAN WHENEVER

check EXACTLY what the question is asking for

like if you need to add 300seconds

deriving an intergral (1rst derivative rule)

usually what you do just replace the t with x or the other way around, but if there’s a -0.8t or something because it’s E(t) -L(t) , you would take the derivative of that as well

• tbh just know what they’re aksing and what each formula represents because this question said that 0.7 people leave per second (which sounmds like rate but it would be in the total number of people in line not the rate equation)

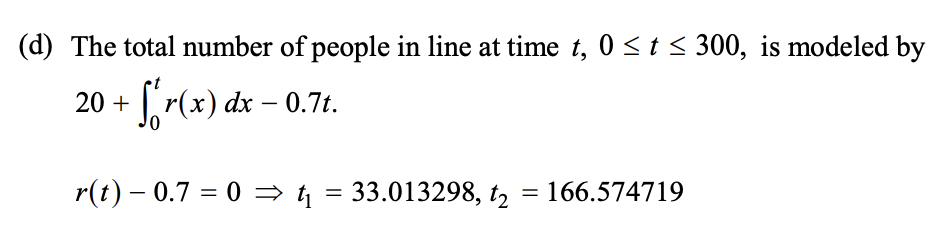
what to do when you see a dø/dt or dø/dr or whawtever something confusing

figure out what d/d they’re asking for

• figure out what d/d you have

• figure out the d/d you need to multiply by/divide by to get the aswer ex. need dø/dt, have dr/dt, find dø/dr

• derive it no matter what