Thermodynamic Work

dx

(1)

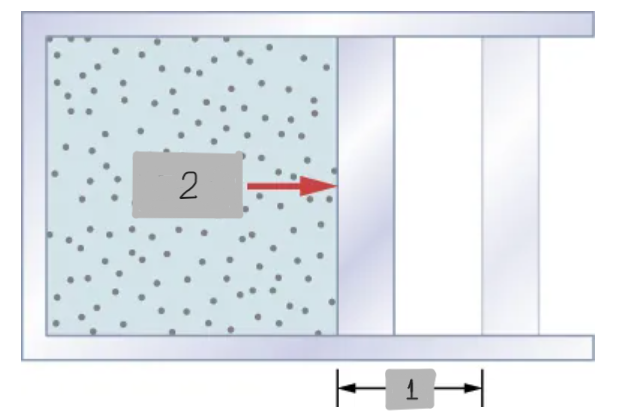
F = pA

(2)

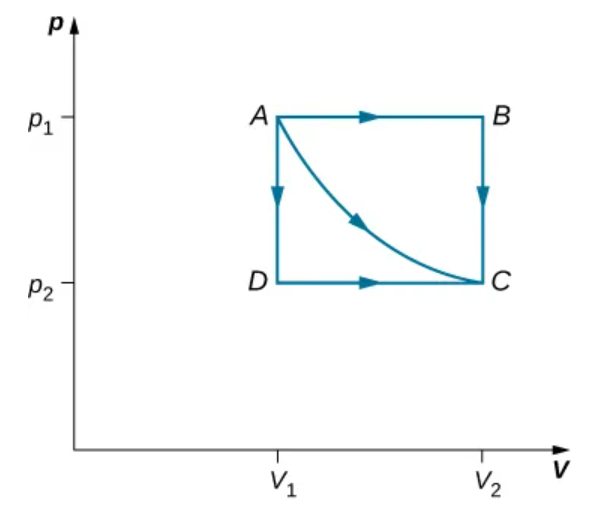
The paths ABC, AC, and ADC represent three different quasi-static transitions between the equilibrium states A and C.

Thermodynamic Work

The work done when a system’s boundary moves under a force, like how, a gas expands or compresses a piston.

dW = pdV

Work done by a Gas (Infinitesimal) represented as Work done by a system during a tiny change in Volume at pressure p

W = ∫(from V1 to V2) pdV

Work Done Over a Finite Volume Change

Positive Work

Gas expands (V2 > V1)

Negative Work

Gas is compressed (V2 < V1)

Quasi-Static Work

A process carried out slowly enough that the system remains in thermal equilibrium at all times, allowing a well-defined p(V) relationship.

Path Dependance of Work

• Work is not a state function

• Different thermodynamic paths between the same two states yield different work values

W = nRTln(V2/V1)

• Isothermal Work (Ideal Gas)

• Only valid when the temperature remains constant

Isobaric Work

Work done during a constant-pressure process.

W = p(V2 - V1)

Mathematical representation of the Isobaric Work

Internal Energy (Eint)

The sum of all microscopic kinetic and potential energies of all particles in the system.

Components of Molecular Kinetic Energy

Includes translational, rotational, and vibrational kinetic energy of molecules.

Components of Molecular Potential Energy

Associated with intermolecular interactions (negligible for an ideal gas)

Eint = (3/2)nRT

Internal Energy of an Ideal Monoatomic Gas. (Depends only on the Temperature)

K̅ = (3/2)((k_B)T)

Average Translational Kinetic Energy per Molecule

translational kinetic energy

In an ideal monoatomic gas, only __________________________ contributes to the internal energy, rotational, vibrational and intermolecular potential energies are absent.

redistribute, energy, collisions

Molecules ____________ ______ through __________ until both gases reach the same temperature (thermal equilibrium)

Yes it is true

Is it true that for an ideal monoatomic gas, temperature directly determines average kinetic energy and therefore internal energy.

No Effect of Bulk Motion on Internal Energy

Internal energy does not depend on system’s location or macroscopic motion (e.g., moving the gas to a higher floor does not changes the Eint).

Work By The Gas

Expansion → Gas pushes surroundings.

Work On The Gas

Compression → Surroundings push the gas

pV diagram

• A plot of pressure v/s volume used to visualize processes

• Area under the curve equals the work done by the gas.

Isothermal Process

• Thermodynamic process during which temperature remains constant

• Internal energy stays constant for ideal gases.