Stat nice

Zákon rozdělení náhodné veličiny

říká, že každé hodnotě nebo množině hodnot z každého intervalu přiřazuje pravděpodobnost, že náhodná veličina nabude této hodnoty z určitého intervalu

hustota pravděpodobnosti se spočte jako

derivace distribicni funkce

jak vypadaji centralni momenrty

Rozptyl - jaky je to moment a jak vypocitat

druhy centralni moment + obrazek

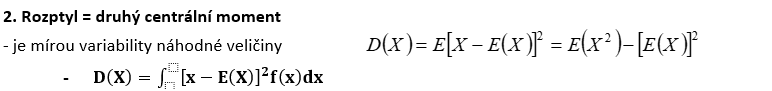
kovariance

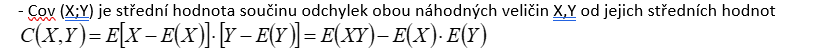
Konvergence podle pravděpodobnosti k náhodné veličině

Konvergence podle pravděpodobnosti ke konstatntě a

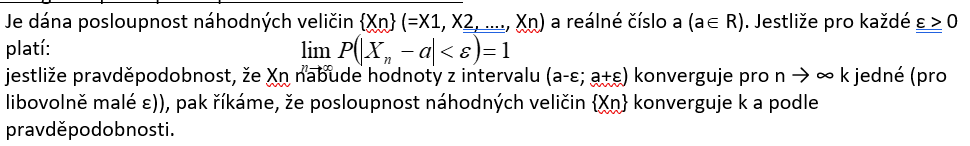
Čebyševova nerovnost I. typu

Čebyševova nerovnost II. typu

Zákon velkých čísel

• jestliže zvětšujeme počet náhodných pokusů, přibližuje se empirická charakteristika, popisující výsledky těchto pokusů, charakteristice teoretické

• musíme si uvědomit, že přibližování empirických hodnot k teoretickým nemá charakter matematické konvergence, ale konvergence pravděpodobnostní. Pravděpodobnostní konvergencí rozumíme skutečnost, že při vzrůstajícím počtu pokusů se pravděpodobnost větších odchylek empirických hodnot od teoretických stále zmenšuje

• Bernoulliho veta/Čebyševova věta

Bernoulliho věta

• Bernoulliho věta říká, že relativní četnost sledovaného jevu stochasticky konverguje k jeho pravděpodobnosti, význam této věty spočívá v možnosti experimentálně odhadovat neznámou pravděpodobnost pomocí napozorované relativní četnosti

Čebyševova věta

silny zakon velkých cisel

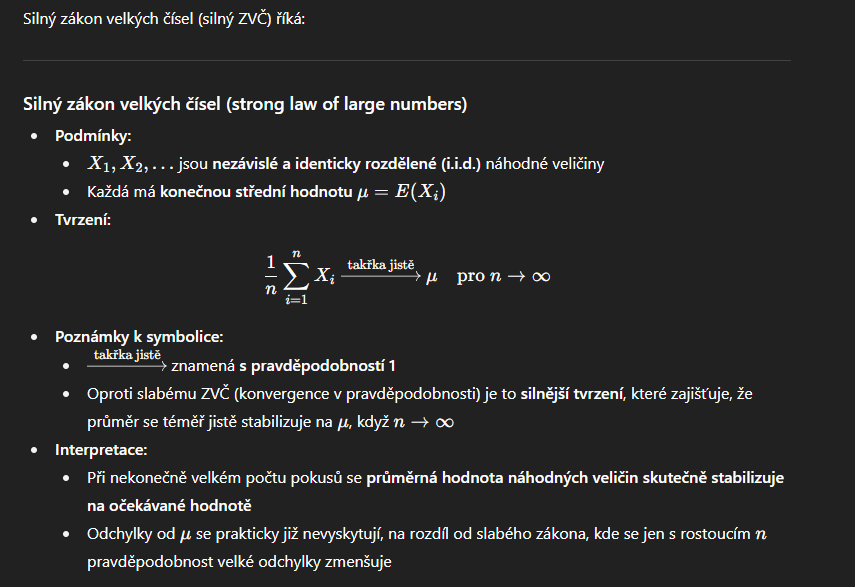
Centrální limitní věta

• říká, že součet nebo průměr velkého počtu nezávislých náhodných veličin se přibližuje k normálnímu rozdělení, bez ohledu na původní rozdělení jednotlivých veličin.

• Moivre-Laplace/Linderberg-Lévy

Moivre-Laplace věta

• Speciální případ CLT pro binomické rozdělení

• umožňuje převést diskrétní binomické pravděpodobnosti na spojité normální rozdělení.

• Velké binomické experimenty (např. 100 a více hodů) lze snadno analyzovat bez nutnosti počítat složité binomické koeficienty.

Lindenberg-levy

• Obecná verze centrální limitní věty (CLT) pro i.i.d. veličiny náhodnou veličinou X je v tomto případě součet n nezávislých náhodných veličin, které mají libovolný identický zákon rozdělení s konečnou střední hodnotou E(X_i) = µ a konečným rozptylem D(X_i) = σ², i =1,2,3,…,n

• podle této věty má pro dosti velké n přibližně normální rozdělení i součet a průměr n nezávislých náhodných veličin, které mají stejné (libovolné) rozdělení s konečnou střední hodnotou a konečným rozptylem

fisherova informace a ramerova craova nerovnost

Trimean

počítá vážený aritmetický průměr kvartilů, mediánu dává váhu 0,5 a kvartilům váhu 0,25.

trimean = 0,25*dolní kvartil + 0,5*medián + 0,25* horní kvartil

Windsorizovaný průměr

se používá tehdy, pokud soubor obsahuje extrémní hodnoty, ale jde o soubor malého rozsahu, kdy useknutí značným způsobem snižuje rozsah souboru. Při výpočtu windsorizovaného průměru v uspořádaném výběru nejprve nahradíme předem zvolený počet nejmenších hodnot ve výběru hodnotou následující a stejný počet největších hodnot nejbližší předcházející hodnotou. V takto upraveném výběru pak určíme aritmetický průměr

Useknutý průměr

aritmetický průměr uspořádaného výběru po vynechání zvoleného počtu (k) nejmenších a největších pozorování. Nevýhodu je, že o část pozorování přijdu (není zachován výběr o rozsahu n).

MAD

MAD představuje míru variability, která je jenom málo ovlivněna extrémními hodnotami (medián je méně citlivý na odlehlé hodnoty než aritmetický průměr).

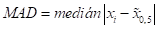
Giniho koeficient

je charakteristikou nerovnoměrnosti (rozptýlenosti). Jde o průměrnou vzdálenost mezi 2 pozorováními. Giniho koeficient nabývá hodnot od 0 do 1.

VARIAČNÍ KOEFICIENT

Relativní mira variability = s/průměr x

Glivenkova věta

• Glivenko–Cantelliho věta poskytuje teoretický základ pro uniformní konvergenci odhadů distribuční funkce, na kterou KDE navazuje.

• Díky tomu lze používat jádrové odhady hustoty jako konzistentní odhady hustoty a distribuční funkce.

• Prakticky: pro velký vzorek f^n(x)\hat{f}_n(x)f^​n​(x) i integrovaná F^n(x)\hat{F}_n(x)F^n​(x) jsou velmi blízko skutečné f(x)f(x)f(x) a F(x)F(x)F(x).

Kolmogorov smirnov test

1 výběr: H0: dle EDF říkáme, že F(x) = F(x)’

• test kritérium: vzdálenost těchto funkcí

2 výběry: H0: F1(x) = F2(x)

• test kritérium: vzdálenost mezi nimi

Test dobré schody

• shody četností(kategoriální data)/shody rozdělení četností(kvantitativní data)

• porovnání F(x) výběru a normálně rozdělené F(x)

• Chí kvadrát test dobré schody

  • posouzení rozdílu mezi empirickými četnostmi výskytu hodnot a očekávanými četnostmi odpovídajícímu danému rozdělení(Normálnímu)

  • H0: NV má normální rozdělení

slaba sada predpokladu

nulovy prumer, konstatntni rozptyl a nekorelovanost

pokud je splnuje chybova slozka, pak odhady MNČ=odhadny ML

Analyza rozptylu (vzprce + cista chyba a nedostatek shody )

Identifikac eodlehlých pozorobání

diagonální prvky matice h, normované rezidua, vnitřně/vnějšně studentizovaná rezidua

identifikace vlivných pozorování

cookova vzdalenost

Bartlettův test

• nekonstruktivní testy heteroskedasticity

Leveneův test a Brown-Forsythův test

• nekonstruktivní testy heteroskedasticity

Goldfeld-Quandtův test

gLEJSRŮV TEST

Důsledky heteoskedasticity

• Pro malý počet pozorování – odhad zůstává nestranný, ale není vydatný

• Pro velký počet pozorování – odhad je asymptoticky nestranný a konzistentní, ale není asymptoticky vydatný

• IS a testovací hypotézy ztrácí na síle → doporučuje se použít jinou metodu než MNČ, a to ZMNČ (zobecněnou MNČ)

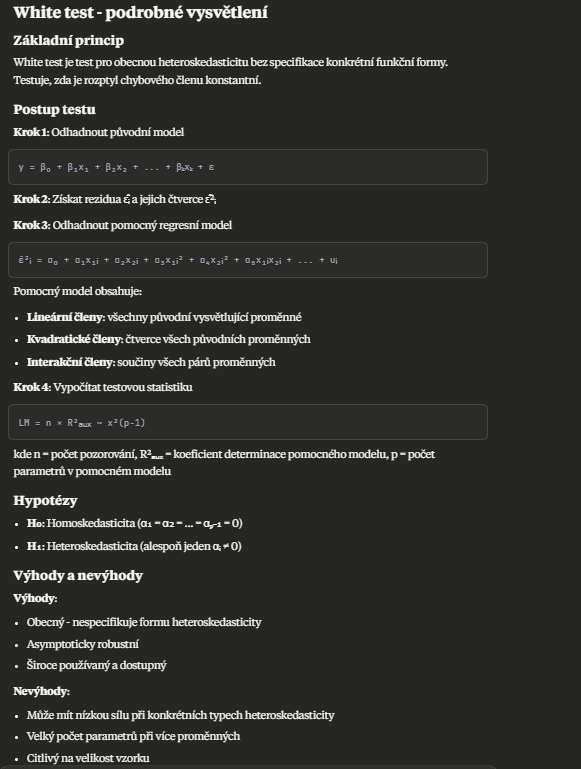
White TEST

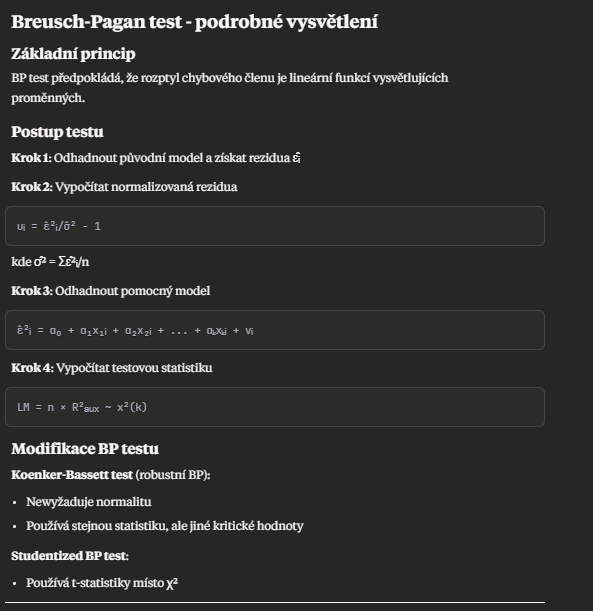
BP test

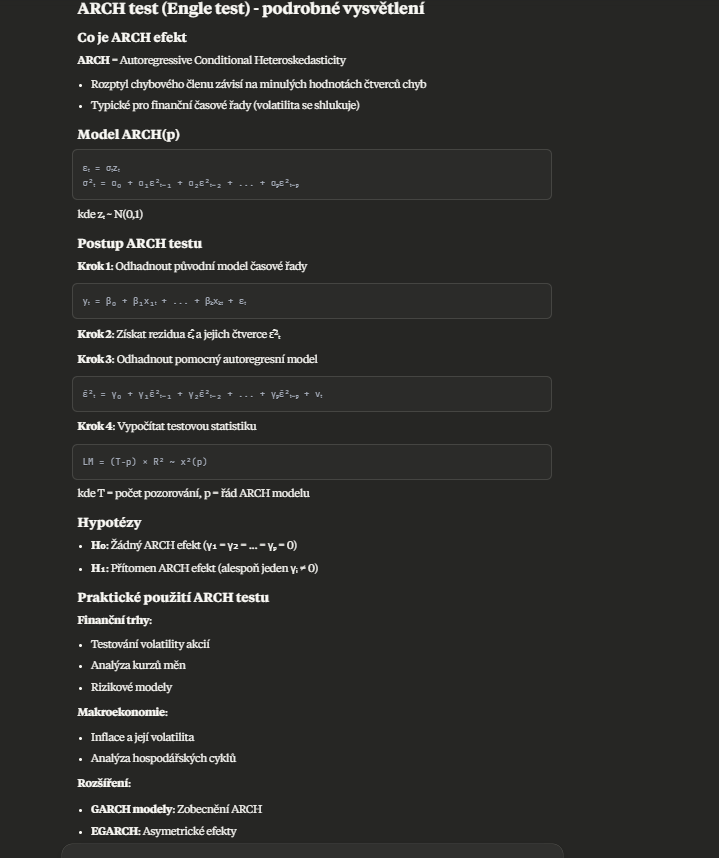
ARCH test

ljung box test

Breutsch-Godrey test

špatná specifikace modelu

• vynechání proměnné

  • odhady koeficientu vychyleny (unless by byly promenne totalne nezavisle)

  • rozptyl nižší než by měl být

• zahrnutí proměnné

  • odhady nejsou vydatné (rozptyly větší) - > rozšířené IS

  • mulitkolinearita

• Šparný typ fce

RESET

Regression specification error test

interval vs pomer veůicina

Intervalová veličina:

• Je charakterizována tím, že mezi jednotlivými hodnotami existuje konstantní rozdíl, ale nulový bod je pouze arbitrární (určený dohodou).

• Příklady: teplota ve stupních Celsia, rok narození.

• Nulový bod (např. 0 °C) neznamená absenci tepla. Rozdíl mezi 20 °C a 30 °C je stejný jako rozdíl mezi 10 °C a 20 °C, ale nelze říci, že 20 °C je dvakrát tak teplé jako 10 °C. 

Poměrová veličina:

• Má nulový bod, který skutečně znamená "nic".

• Příklady: výška, váha, věk, počet dětí v rodině, měsíční příjem.

• Pokud má někdo výšku 180 cm a jiný 90 cm, lze říci, že první je dvakrát tak vysoký. Nula centimetrů znamená absenci výšky. 

Simultánní IS - Hotelling vs Bonferroni

·        Jsme-li předem rozhodnuti zaměřit se na jednu složku vektoru µ => individuální IS

·        Jsme-li předem rozhodnuti zaměřit se na několik složek, popřípadě všechny složky => Bonferr. simul. IS

·        Počítáme-li s určitým pátráním v datech, takže nejsme předem zaměření na daný počet lineárních kombinací složek vektoru µ → simultánní IS T²

Testování vektorů středních hodnot - 2nezávislé výběry

 Neznámé kovarianční matice jsou shodné

• mu1-mu2=0

• pro srovnání vektorů použijeme hottelinga nebo bonferroniho intervaly

Nestejné kovarianční matice

• mu1-mu2=0

• Scheffuv test

Testování vektorů středních hodnot - 2 závislé výběry

jedna proměnná

• párové rozdíly, H0: muD = 0

vÍCE PRoměnných

• to samé, ale s maticí

• při zamítnutí můžeme koukat na důvod úřes bonferroniho IS

mallowsova statistika

cista chyba a nedosztatelk shody

1. Čistá chyba (pure error)

• Vzniká, když máme opakovaná pozorování pro stejné hodnoty vysvětlujících proměnných.

• Měří náhodný rozptyl dat, který by existoval i při perfektním modelu.

• Čistá chyba = variabilita uvnitř replikací (mezi pozorováními se stejným xxx).

• Nezávislá na volbě modelu.

---

2. Nedostatek shody (lack of fit)

• Vzniká, když zvolený regresní model není dostatečně flexibilní k popisu vztahu mezi yyy a xxx.

• Měří odchylku mezi průměry pozorovaných hodnot pro stejné xxx a hodnotami předpovězenými modelem.

• Ukazuje, zda model správně vystihuje tvar závislosti.

jednofaktorova anova vicefaktrova anova jednofaktorova manova vicefaktorova manova

• V ANOVA: H0H_0H0​ = rovnost skalárních průměrů.

• V MANOVA: H0H_0H0​ = rovnost vektorů průměrů (tedy všech závislých proměnných současně).

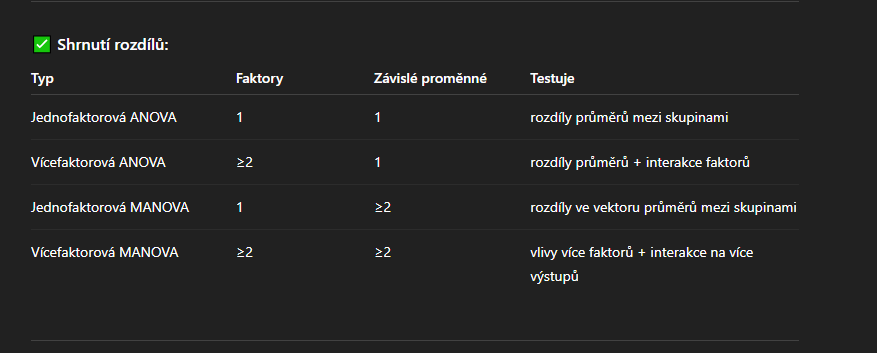
jaka TEST statistika je pro anova/manova

pevne vs nahodne efekty v anove/manove

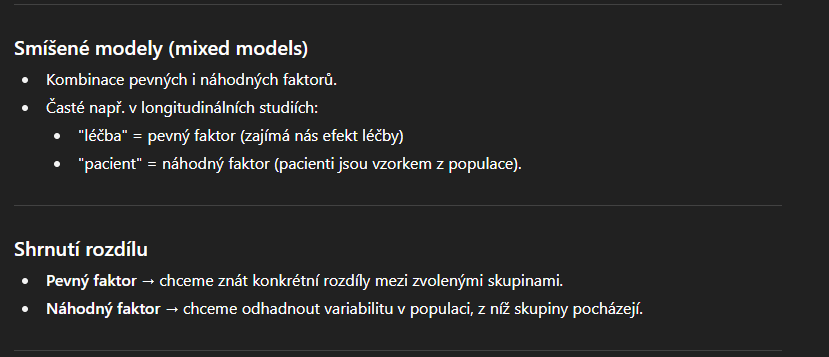
Typy součtu čtverců v GLM

pca vs fa

·        PCA:

§  výhodnější vycházet z analýzy kovarianční matice, pokud mají proměnné stejné měřící jednotky a relativně podobnú variabilitu

§  hledá komponenty, které vysvětlují variabilitu a závislost uvažovaných proměnných

·        FA:

§  výhodnější vycházet z analýzy korelační matice

§  hledá faktory, které vysvětlují variabilitu a závislost uvažovaných proměnných

komponentni skore

Reprezentuje položení jednotlivých pozorování v prostoru hlavních komponent.

Vektory komponentních zátěží (loadings)

• Udávají váhy původních proměnných v jednotlivých komponentách.

• Jsou to vlastních vektory viv_ivi​ matice kovariancí/korelační matice.

• Rozměr: p×pp \times pp×p (počet proměnných × počet komponent).

• Slouží k interpretaci, které proměnné nejvíce přispívají k dané komponentě.

Bartlettův test sfericity v PCA

• diagnostika vhodnosti dat pro PCA.

• H0​:Korelacˇnıˊ matice je jednotkovaˊ (identickaˊ)

• H1​:existujıˊ korelace mezi promeˇnnyˊ​mi

kmo

kaiser-eyer-olkin

• Hodnotí míru korelace mezi proměnnými relativně k jejich parciálním korelacím.

• Zjednodušeně: měří, zda jsou korelace mezi proměnnými dostatečně silné, aby byla PCA/faktorová analýza smysluplná.

• vysoké kmo → pca/fa

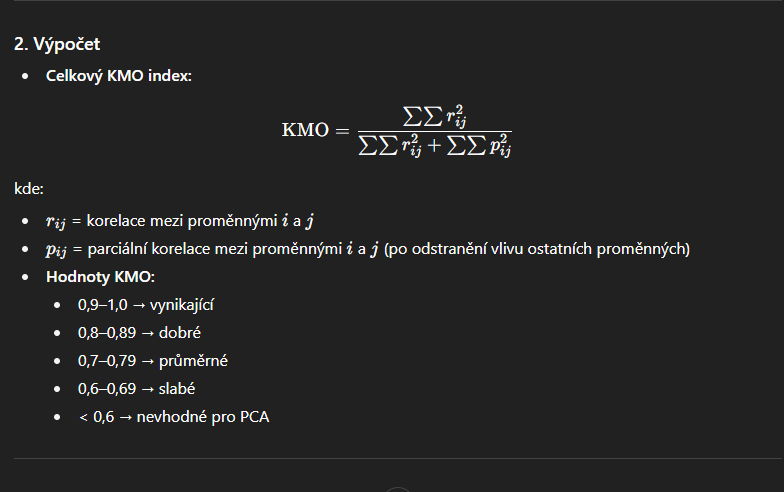
komuniality v pca

komunality (communality) ukazatelem toho, kolik variability původní proměnné je vysvětleno vybranými hlavními komponentami.

Faktorská analýza – metoda hlavních faktorů

• Odlišuje se od PCA tím, že se soustředí jen na společnou (komunalitní) složku variability, nikoli celkovou variabilitu.

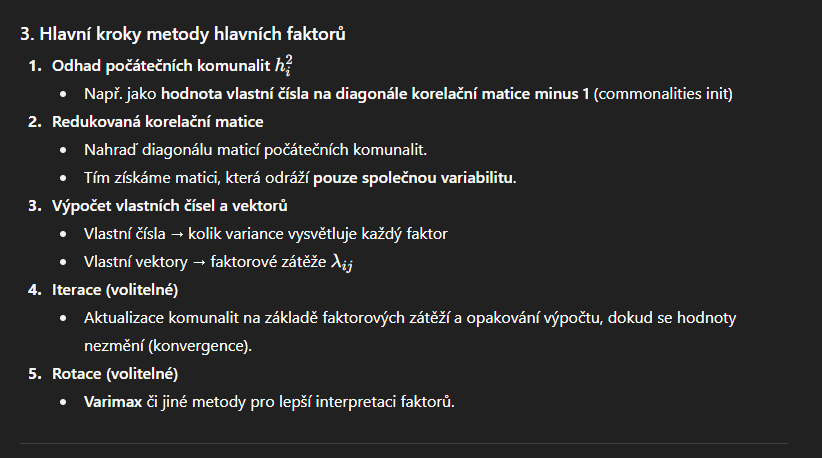
Rotace ve faktorce

1. Cíl rotace

• Získat interpretovatelnější faktorovou strukturu.

• Minimalizovat počet významných zátěží na jednom faktoru a maximalizovat jasnost přiřazení proměnných k faktorům.

---

2. Typy rotací a) Ortogonální rotace

• Faktory zůstávají navzájem kolmé (nekorelované).

• Nejčastější metody:

  • Varimax – maximalizuje rozptyl čtverců faktorových zátěží, snaží se, aby každá proměnná měla jednu dominantní zátěž.

  • Quartimax – zjednodušuje strukturu pro proměnné (méně faktorů s vysokými zátěžemi).

  • Equamax – kombinace Varimax a Quartimax.

b) Šikmé (oblique) rotace

• Faktory mohou být korrelované.

• Metody: Promax, Oblimin.

• Používá se, pokud existuje teoretické očekávání, že latentní faktory jsou vzájemně propojené.

Průběh faktorky

1. Příprava dat

• Data: matice XXX (n × p), n pozorování, p proměnných.

• Volitelná standardizace:

  • Nutná, pokud proměnné mají různé jednotky.

2. Výpočet korelační matice

• Faktorka se obvykle provádí na korelační matici RRR, protože:

  • Eliminujeme problém odlišných jednotek.

  • Získáme měřítkově nezávislé výsledky.

• Alternativně lze použít kovarianční matici, pokud všechny proměnné jsou ve stejné jednotce.

3. Odhad společné variance (communalities)

• Na začátku se často nastaví:

  hi2=1(pro PCA-based start)h_i^2 = 1 \quad \text{(pro PCA-based start)}hi2​=1(pro PCA-based start)

  • Každá proměnná je považována za zcela společnou.

• Můžeme také použít menší hodnoty (např. extrahovat první hlavní komponentu a použít její varianci).

4. Eigen-decomposition

• Rozklad korelační matice RRR (s odhadem společných variancí):

  R=VΛVTR = V \Lambda V^TR=VΛVT

  • Λ\LambdaΛ – vlastní čísla (eigenvalues)

  • VVV – vlastní vektory (loadings)

• Počet faktorů mmm určuje:

  • Eigenvalues > 1 (Kaiserovo kritérium)

  • Scree plot (zlom v křivce)

  • % vysvětlené variance

5. Výpočet faktorových zátěží (factor loadings)

• Zátěže LLL jsou odvozeny z vlastních čísel a vektorů:

  L=VmΛm1/2L = V_m \Lambda_m^{1/2}L=Vm​Λm1/2​

  • VmV_mVm​ – vlastní vektory vybraných mmm faktorů

  • Λm\Lambda_mΛm​ – odpovídající vlastní čísla

• Faktorové zátěže ukazují vztah mezi proměnnou a faktorem.

6. Iterativní odhad společných variancí (volitelné)

• Pokud se používá principal factor method (ne čisté PCA):

  1. Začneme s počátečními komunalitami hi2h_i^2hi2​

  2. Extrahujeme faktory

  3. Aktualizujeme komunality:

     hi2=∑j=1mLij2h_i^2 = \sum_{j=1}^{m} L_{ij}^2hi2​=j=1∑m​Lij2​

  4. Iterujeme, dokud se komunality nezmění významně

7. Výpočet faktorových skóre

• Faktorové skóre pro jednotlivá pozorování F=Z⋅WF = Z \cdot WF=Z⋅W, kde WWW je váhová matice odvozená z LLL

• skóre ukazuje, jak jednotlivá pozorování „leží“ na faktorech

8. Rotace faktorů (volitelné)

• Pro lepší interpretaci:

  • Ortogonální rotace: varimax, quartimax

  • Šikmá rotace: oblimin, pro korelované faktory

• Rotace maximalizuje vysoké zátěže a minimalizuje nízké, čímž faktory lépe odpovídají proměnným

9. Interpretace

• Factor loadings → co jednotlivé faktory reprezentují

• Communalities → kolik variance každé proměnné je vysvětleno faktory

• Factor scores → umístění jednotlivých pozorování v prostoru faktorů