Geometry HN - Unit 2: Logic and Reasoning

Counter example

An example that shows your conjecture is false

Inductive

Drawing a conclusion based on observations or patterns

Conjecture

A conclusion drawn using inductive reasoning

Negation

A negation of a statement has the opposite truth value

Compound statements

Statements joined by “and” or “or”

/\

and

\/

or

T/\T

True

T/\F

False

F/\F

False

T\/T

True

T\/F

True

F\/F

False

Conditional statement

Written in if-then form. The hypothesis is before if and conclusion is after then.

Inverse

Formed by negating the hypothesis and conclusion (~p→~q)

Converse

Formed by switching the hypothesis and conclusion (q→p)

Contrapositive

Formed by negating and switching the hypothesis and conclusion (~q→~p)

Logically equivalent

Two statements are logically equivalent they have the same true value (converse and inverse, conditional and contrapositive)

Bi-conditional statements

Conditional & converse joined by a conjuncition

Valid argument

When the conclusion necessarily follows from the given set of premises.

Invalid agrument

When the conclusion does not necessarily follows from the given set of premises

Fallacy

An invalid argument

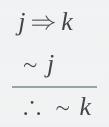
What standard form of argument is this?

Fallacy of the Inverse (invalid)

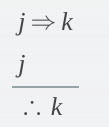
What standard form of argument is this?

Fallacy of the Detachment (valid)

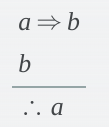
What standard form of argument is this?

Fallacy of the Converse (invalid)

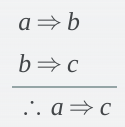
What standard form of argument is this?

Law of Syllogism (valid)

What standard form of argument is this?

Law of Contrapositive (valid)

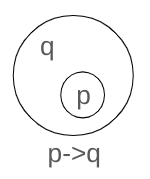
All, Always, Every

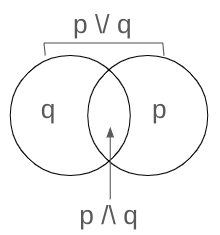
Some, Sometimes

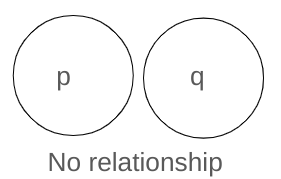
Never, No, None

If a=b, then a+c=b+c.

Addition Property of Equality (APE)

If a=b, then a-c=b-c.

Subtraction Property of Equality (SPE)

If a=b, then a⋅c=b⋅c.

Multiplication Property of Equality (MPE)

If a=b, then a/c=b/c. (c≠0)

Division Property of Equality (PPE)

a(b+c)=ab+ac

Distributive Property

If a=b then a may be replaced by b in any expression or equation.

Substitution Property

For any real number, a, a=a. (A value will always equal itself)

Reflexive Property

If a=b, then b=a.

Symmetric Property

If a=b and b=c, then a=c.

Transitive Property

Applied to statements with congruence symbols. (≅)

Properties of Congruence

For any segment AB, AB≅AB.

Reflexive Property of Congruence (RPC)

If AB≅CD, then CD≅AB.

Symmetric Property of Congruence (SPC)

If AB≅CD and CD≅EF, then AB≅EF.

Transitive Property of Congruence (TPC)

Segments are congruent if and only if they have the same measure.

If AB≅CD, then AB=CD.

If AB=CD, then AB≅CD.

Definition of Congruence

If M is the midpoint of AB, then AM=BM.

Definition of Midpoint

If A, B, and C are collinear points and B is between A and C then: AB+BC=AC.

Segment Addition Postulate. (SAP)

m∠A=m∠B🡘∠A≅∠B.

Definition of Congruence.

An angle bisector divides an angle into two equal parts.

Definition of Angle Bisector

Complementary 🡘 sum is 90°.

Definition of Complementary Angles

Supplementary 🡘 sum is 180°.

Definition of Supplementary Angles

Perpendicular lines form right angles.

Definition of Perpendicular.

A right angle=90°.

Definition of Right Angle

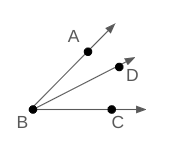
m∠ABD+m∠DBC=m∠ABC

Angle Addition Postulate (AAP)

If two angles are vertical, then they are congruent.

Vertical Angle Theorem

If two angles form a right angle, then they are complementary.

Complement Theorem

If two angles form a linear pair, then they are supplementary.

Supplement Theorem (Linear Pair Postulate)

If ∠A is complementary to ∠B and ∠C is complementary to ∠B, then ∠A≅∠C.

Congruent Complements Theorem

If ∠A is supplementary to ∠B and ∠C is supplementary to ∠B, then ∠A≅∠C.

Congruent Supplements Theorem