Unit 7 - One Sample Significance Tests

Includes Unit 9.

H ₀

Null hyp. p=null value. “expect no change”

p

true prop. (context)

Ha

Alt. hyp. One-sided: p< null value, p>null value. Two sided: p doesn’t equal null value. “expect change”.

Interpret p-value for Sig. Test

Assuming Ho is true (p=), there is a P-VALUE prob. of getting a ^p of X or greater/less purely by chance.

Conclusion for Sig. Test

Because (p-value>a / p-value<a), we (fail to reject Ho / reject Ho), and we (don’t / do) have convincinf evidence for Ho (context).

Full conclusion for a significnce test:

1. Interpret p-value. 2. Conclusion.

Conditions for One Sample z-test for p.

1. Random 2. 10% 3. LCC

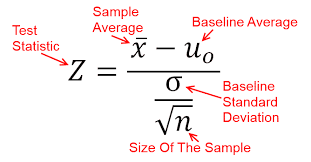
Calculations for Sig. Tet for one-sample z-test for p.

Test statistics (z-score) and p-value (use normalcdf)

4-Step Process for Sig. Test for Proportion

STATE: one-sample z-test for p, parameter, Ho, Ha, stat, alpha. PLAN: random, 10%, LCC. DO: general and specific formula, plug-in, picture, test stat, z-score, CONCLUDE: decision & conclusion (in context).

If two-sided Ha

Ha: p doesn’t equal null. Must multiply p-value by 2.

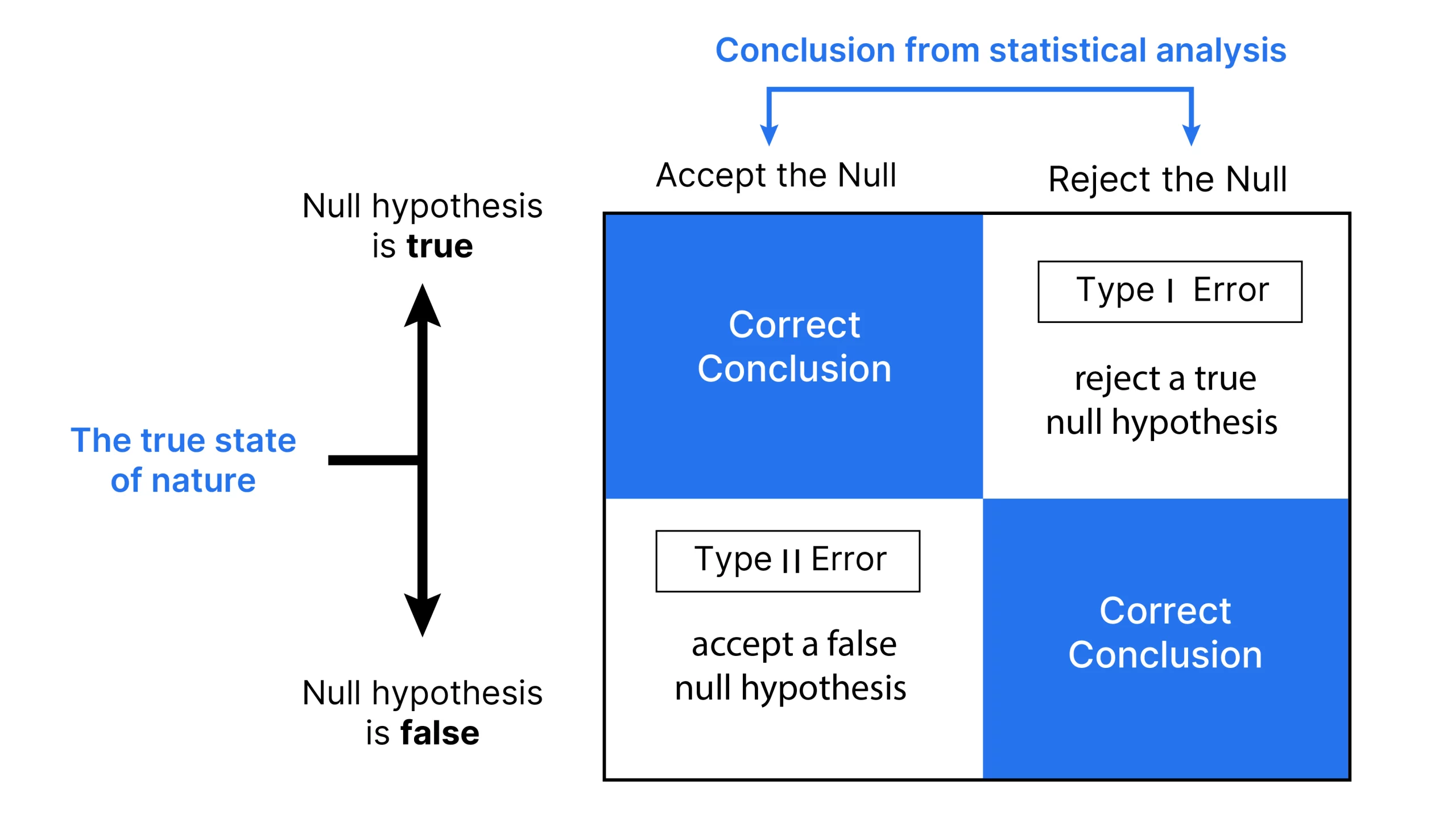
Type 1 Error + Intpreation formula

Ho true. Reject Ho. P(Type 1) = alpha. “The null hypothesis (context) is true, but we find convincing evidence for Ha (context).”

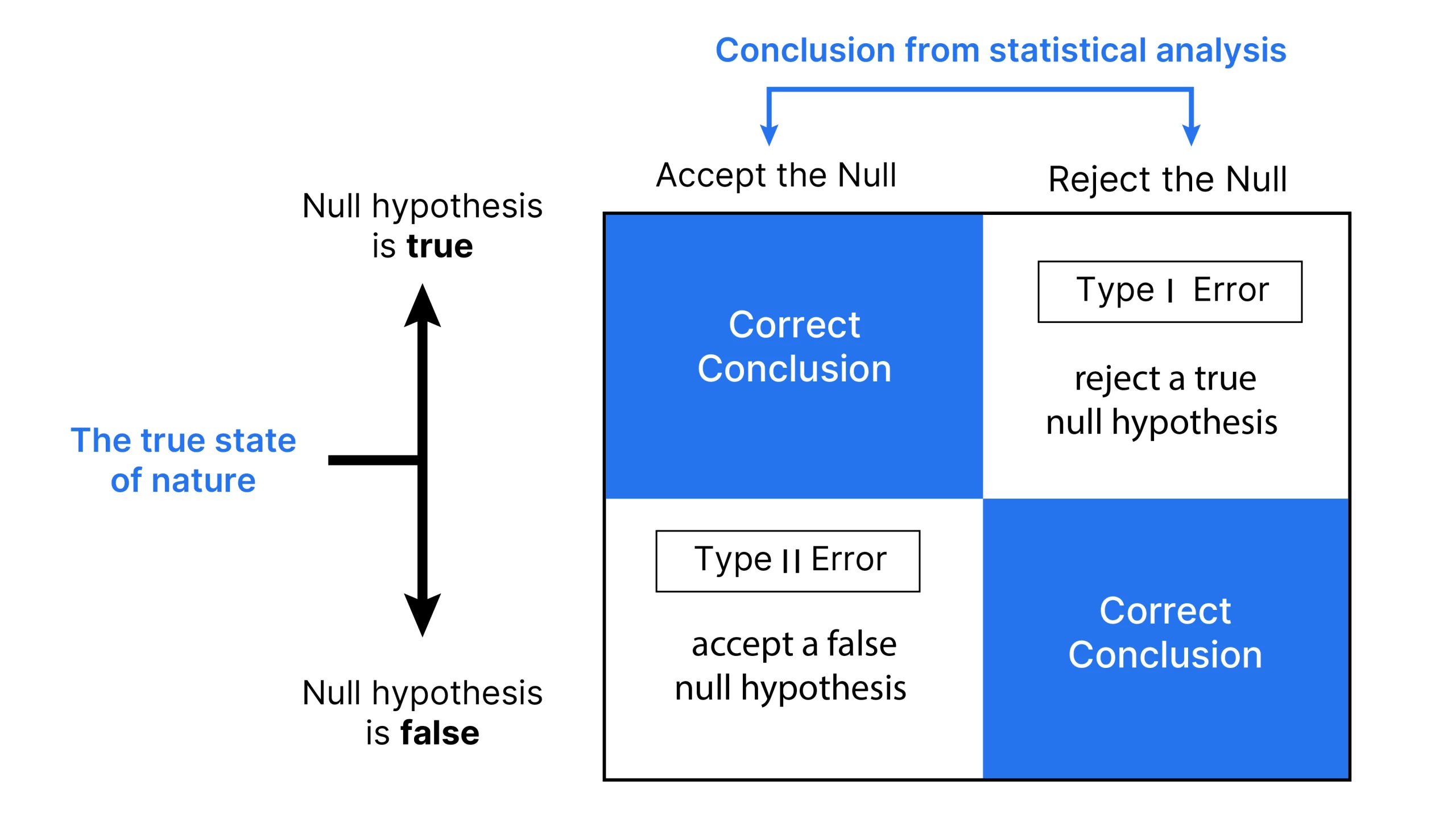
Type 2 Error + Interpreation formula

Ha true. Fail to reject Ho. “The alt. hyp. (context) is true, but we don’t find convincing evidence for Ha (context.”

To decrease probability of Type I Errors

Decrease significance level (a).

To decrease probability of Type II Errors

Increase probability of Type I Errors by increasing significance level (a).

Sig. Test Conditions for One Sample t-test for u.

1. Random. 2. 10% 3. Normal: - No large skew/outliers. - CLT. - Approx. Normal.

To find p-value for One Sample t-test for u on calculator use:

T-test or tcdf (lower, upper, df).

Purpose of One-Sample Z-test

Distance, in SD, b/t ^p andpp given p. From that distance, probabilities (a p-value) can be calculated and a claim can be assessed.