GCSE Maths - Edexcel

Finding the LCM of two numbers when you have the prime factors

- List all the prime factors out

- If a factor appears more than once, list it that many times, e.g. 2, 2, 2, 3, 4 and 2, 2, 3, 4 would be 2, 2, 2, 3, 4

- Multiply these together to get the LCM

Finding the HCF of two numbers when you have the prime factors

- List all the prime factors that appear in both numbers

- Multiply these together

Multiplying fractions

Multiply the top and bottom separately

Dividing fractions

Turn the second fraction upside down then multiply

Rule for terminating and recurring decimals

If the denominator has prime factors of only 2 or 5, it is a terminal decimal

Turning a recurring decimal into a fraction

- Name the decimal with an algebraic letter

- Multiply by a power of ten to get the one loop of repeated numbers past the decimal point

- Subtract the larger value from the single value to get an integer

- Rearrange

- Simplify

Turning a recurring fraction into a decimal when the recurring decimal is not immediately after the decimal, e.g. r = 0.16666...

- Name the decimal with an algebraic letter e.g. r = 0.16666...

- Multiply by a power of ten to get the non-repeating part out of the bracket e.g. 10r = 1.6666...

- Multiply to get the repeating part out of the bracket e.g. 100r = 16.6666...

- Take away the larger value from the smaller one (to get an integer) e.g. 100r - 10r = 90r = 15

r = 15/90

- Simplify e.g. 15/90 = 1/6

Turning a fraction into a decimal

- Make the fraction have all nines at the bottom

- The number on the top is the recurring part, the number of nines is the number of recurring decimals there are

Significant figures

The first number which isn't a zero. This is rounded.

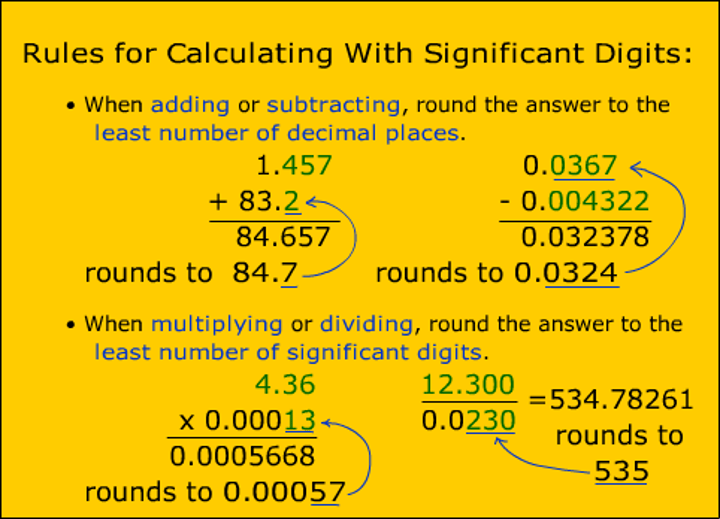
Rules for calculating with significant digits

Estimating square roots

- Find two numbers either side of the number in the root

- Make a sensible estimate depending on which one it is closer to

Truncated units

When a measurement is truncated, the actual measurement can be up to a whole unit bigger but no smaller, e.g. 2.4 truncated to 1 d.p. is 2.4 ≤ x < 2.5

Multiplying and dividing standard form

- Convert both numbers to standard form

- Separate the power of ten and the other number

- Do each calculation separately

Adding and subtracting standard form

- Convert both numbers into standard form

- Make both powers of 10 the same in each bracket

- Add the two numbers and multiply by whatever power of ten; they are to the same power so this can be done

Negative powers

1 over whatever the number to the power was, e.g.

7⁻² = 1 / 7² = 1 / 49

a⁻⁴ = 1 / a⁴

If the number is a fraction, then it is swapped around, e.g.

(3/5)⁻² = (5/3)² = 25 / 9

Fractional powers

Something to the power of 1/2 means square root

Something to the power of 1/3 means cube root

Something to the power of 1/4 means fourth root, e.g.

25^½ = √25 = 5

Two-stage fractional powers

When there is a fraction with a numerator higher than one, spilt it into a fraction and a power and do the root first, then power, e.g.

64^5/6 = (64^1/6)⁵ = (2)⁵ = 32

Difference between two squares

a²-b²=(a+b)(a-b)

Simplifying surds

Split the number in the root into a square number and the lowest other number possible, e.g.

√250 = √(25 × 10) = 5√10

Rationalising the denominator

This is done to get rid of a surd on the denominator. You multiply by the same fraction of the surd, but with the operation the other way round.

Removing fractions when they (the fractions) appear on both sides of an equation

- Multiply by the lowest common multiple of both numbers

- Simplify

Quadratic formula

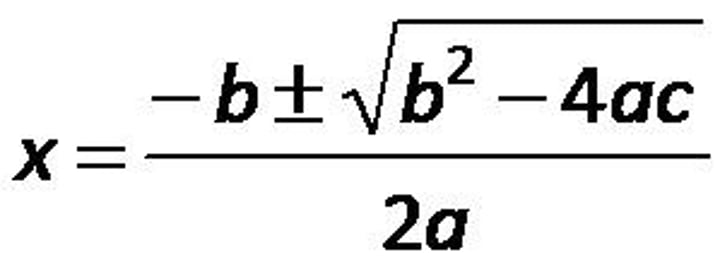
Completing the square

- Write out in the form ax²+bx+c

- Write out the first bracket in the form

(x + b/2)²

- Multiply out the brackets and add or subtract to make the number outside the bracket match the original

Completing the square when 'a' isn't one

- Factorise with the 'a' value outside the brackets

- Write out in the form a(x+b/2)

- Add or subtract the remaining number

Facts about completing the square

For a positive quadratic,

- The number outside the bracket is the y value of a graph

- The number inside the bracket is the x value multiplied by -1

Adding and subtracting algebraic fractions

- Make both denominators equal by multiplying the numerators by the other denominator

- Simplify

Finding the nth term of quadratic sequence

- Find the difference between the difference in each term (this can be called a second difference)

- Divide the second difference by two to get the coefficient of the n² term

- Take away the n² term from the original sequence to get a linear sequence, which can be easily worked out

Algebra with inequalities exception

Whenever you multiply or divide by a negative number, flip the inequality sign round

Inequalities on number lines

- Open circles for < or >

- Closed circles for ≤ or ≥

Quadratic inequalities general rule

- If x² > a² then x > a or x < -a

- If x² < a² then -a < x < a

(this is because with a square root the number can be positive or negative, and the negative would mean flipping the sign)

Drawing quadratic inequalities

- Factorise the equation when it equals zero to find the x intercepts

- Sketch the graph, paying attention to if the x² coefficient is positive or negative

- Solve the equation using the graph, paying attention to whether the original equation is a < or > (or a ≥ or ≤)

- If the equation asks for x > 0, then solve it for where the quadratic is above the x-axis. On a negative graph, this will give the results as -a < x < b, and on a positive graph it will result in x < -a and x > b

- If the equation asks for x < 0, then solve it for when the quadratic is below the x-axis. On a negative graph, the results will be x < -a or x > b, and on a positive graph it would be -a < x < b

- In the picture, the equation is x² - x - 2, as the x intercepts are -1 and 2. The answer to x² - x - 2 > 0 would be x < -1 and x > 2

- If the inequality has a ≤ or ≥ then the final answer has to include a ≤ or ≥ for both roots

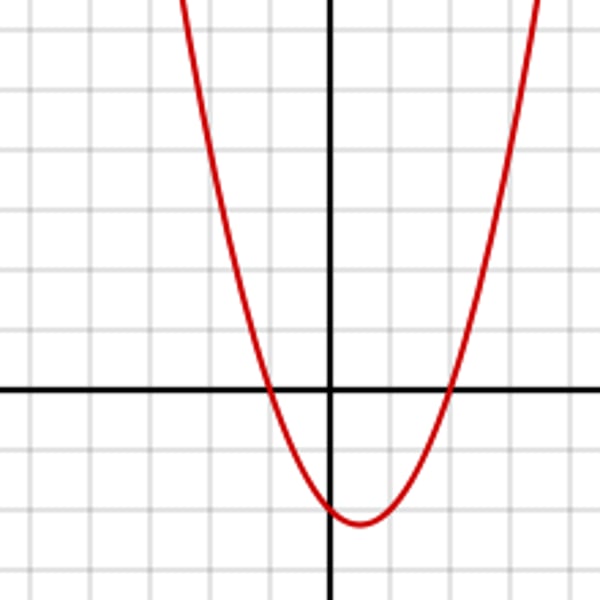
Showing an inequality on a graph

- Convert the inequality into an equation

- Draw the graph for the equation

- Work out which side of the line you want and shade the region which it satisfies (it usually asks in the question)

- If the inequality has a < or >, then draw a dotted line

- If the inequality has a ≤ or ≥, then draw a solid line

Composite functions (e.g. fg(x))

- Always do the function close to x first, e.g. fg(x) would be f(g(x))

Inverse functions (written as f⁻¹(x))

- Write out the equation as x = f(y)

- Rearrange the equation to make y the subject

- Replace y with f⁻¹(x)

Midpoint of two lines

Find the average between the two lines, i.e.

(x₁+x₂/2), (y₁+y₂/2)

Perpendicular lines

These have the gradient -1/m where m is the gradient of the line you are already given

Sketching quadratics

If you have found two roots, you can use symmetry to find out the minimum point or maximum point

Finding the turning point of a circle

Use symmetry of the two x intercepts

Finding the tangent of a circle

- Find the gradient of the point from the centre of the circle to the point on the edge

- This line is perpendicular to the tangent

- Put the values into y = mx + c to find the equation

The equation for a circle

x² + y² = r² where x and y are both points on the circle

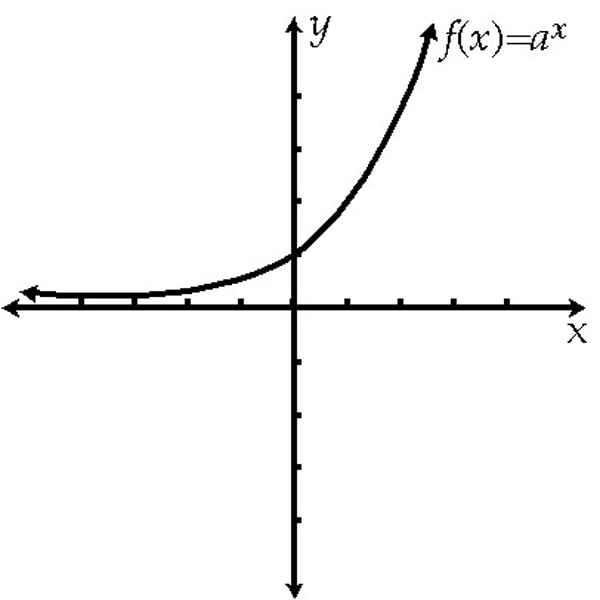
Exponential graphs

y = k^x or y = k^-x

Where the y intercept is always 1

Reciprocal graphs

y = a/x or xy = a

A negative reciprocal would be in the opposite quadrants to the image shown

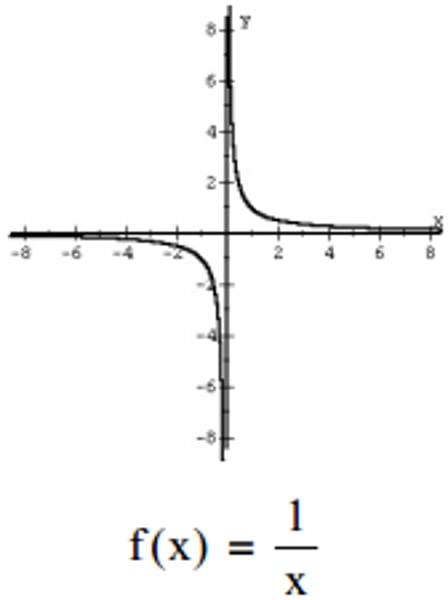
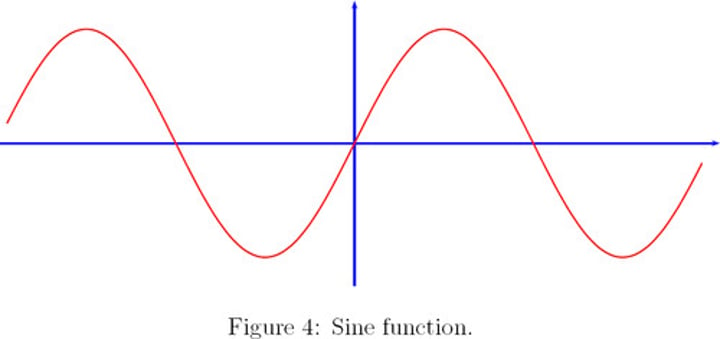
Sine graph (wave)

Cosine graph (bucket)

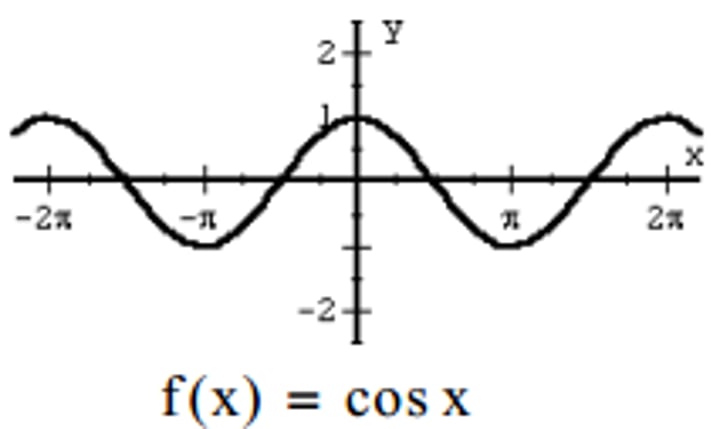
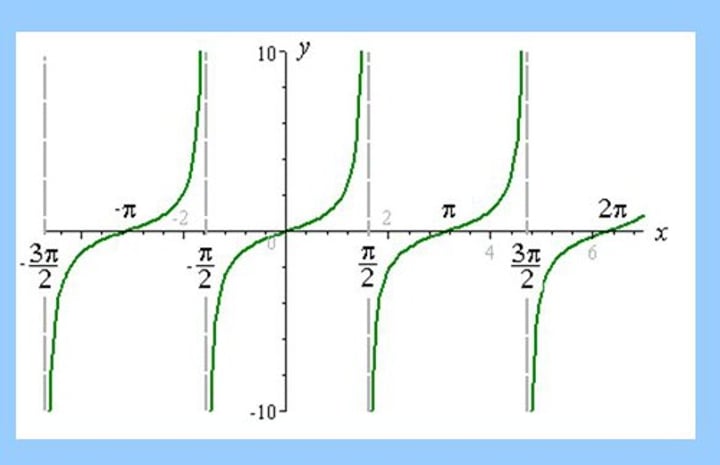
Tan graph

Solving equations using graphs

The points at which they both intersect are the four values to the equations (two values if they are not quadratic). These values have to go together otherwise they do not solve the equations.

Finding the equation of a line you would need if you were to solve another line when you are already given one line

Example:

You are given the graph of y = 2x² - 3x. Find the equation of the line you would need to draw in order to solve 2x² - 5x + 1 = 0

- Rearrange the second function so that you have 2x² - 3x on one side

2x² - 5x + 1 = 0 (-1)

2x² - 5x = -1 (+2x)

2x² - 3x = 2x - 1

Therefore 2x - 1 is the line needed to solve the equation.

y = f(x) + a means

A translation on the y-axis (where a positive a value means the graph goes up)

y = f(x-a) means

A translation on the x-axis (where a positive a value means you go left, or down the x-axis)

y = -f(x) means

A reflection on the x-axis

y = f(-x) means

A reflection on the y-axis

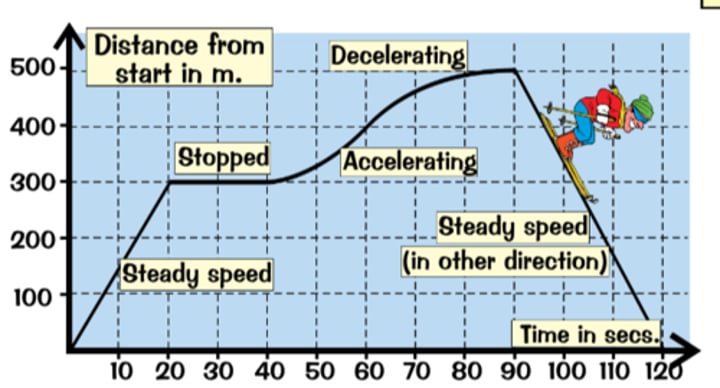
Distance time graphs

- Gradient = speed

- The steeper the graph, the faster

- Flat sections mean it has stopped

- A positive gradient means it is going away from the starting point and vice versa

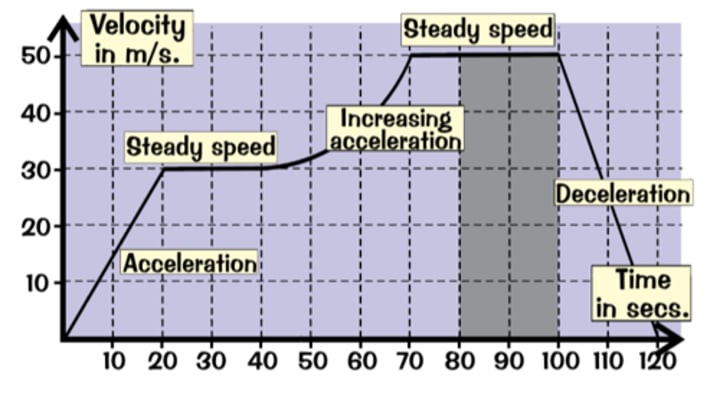
Velocity time graphs

- Gradient = acceleration

- A negative gradient means deceleration

- Flat sections mean a steady velocity

- The area under the graph is the distance travelled

Estimating the area under a graph

- Divide the area into trapeziums of equal length

- Work out the area of each individually

The gradient of a graph represents

The rate (when time is on the x-axis). It is the number of y-axis units over the x-axis units

Finding the average gradient of a curve

Draw a straight line between the two points and find the gradient of that

Estimating the rate at a given point

Draw a tangent at the point required on the curve and work out the gradient

Changing ratios

- Write the ratios as equations

- Write the ratios as fractions

- Solve simultaneously

If y is proportional to x

y = kx

If y is inversely proportional to x

y = k/x

If y is proportional to the square root of x

y = k√x

Simple interest

This means it increases at the same rate each year (the percentage of the original amount)

Compound interest formula

N (amount after n length of time) =

Initial amount × (multiplier)^n number of (unit)

The multiplier is something like 5% = 1.05 etc.

The 'n' (power) is whatever the unit it asks for in the question is

Converting m² into cm²

1 m² = 100 cm × 100 cm = 10 000 cm²

Converting m³ into cm³

1 m³ = 100 cm × 100 cm × 100 cm = 1000000 cm³

Speed formula

Speed = distance / time

Density formula

Density = mass / volume

Pressure formula

Pressure = force / area

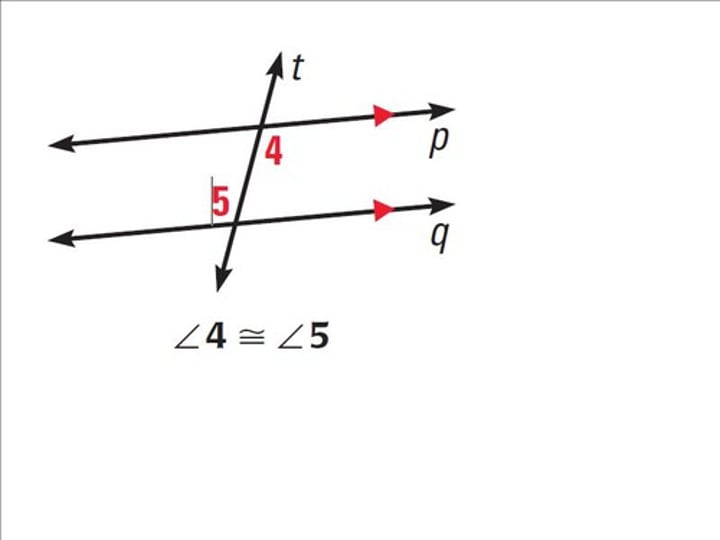
Alternate angles

These are found in a z shape (angle 4 = angle 5)

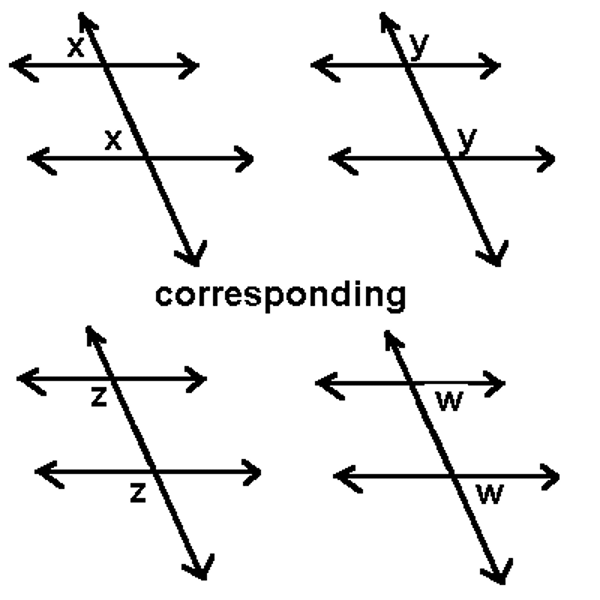
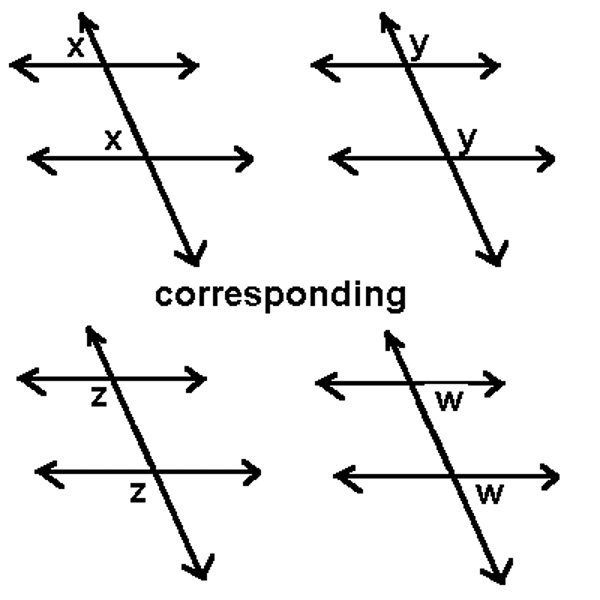
Corresponding angles

These are found in an f shape

Allied angles

These are found in a c or u shape (angle x + angle z = 180)

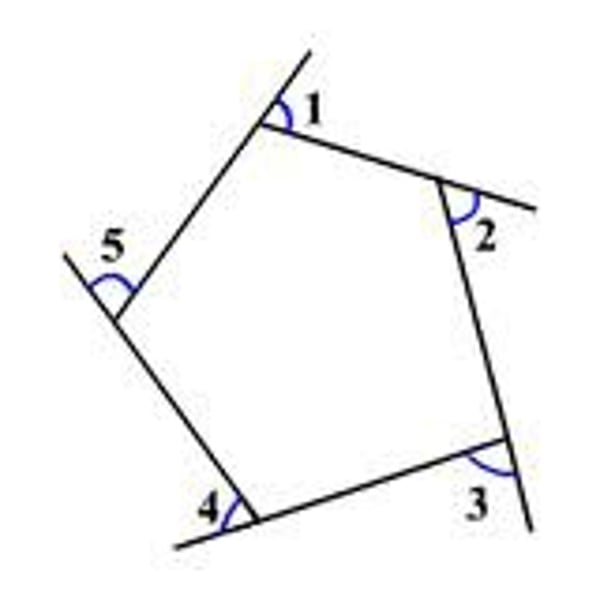
Sum of interior angles

(n - 2) × 180°

Where n is the number of sides

Sum of exterior angles

360°

(In a regular polygon one exterior angle = 360°/n)

Circle geometry rules

- A tangent and radius meet at 90°

- Two radii form an isosceles triangle

- The perpendicular bisector of a chord passes through the centre

- The angle at the centre a circle is twice the angle at the circumference

- The angle in a semicircle is 90°

- Angles in the same segment are equal

- Opposite angles in a cyclic quadrilateral add up to 180°

- Tangents from the same point are the same length

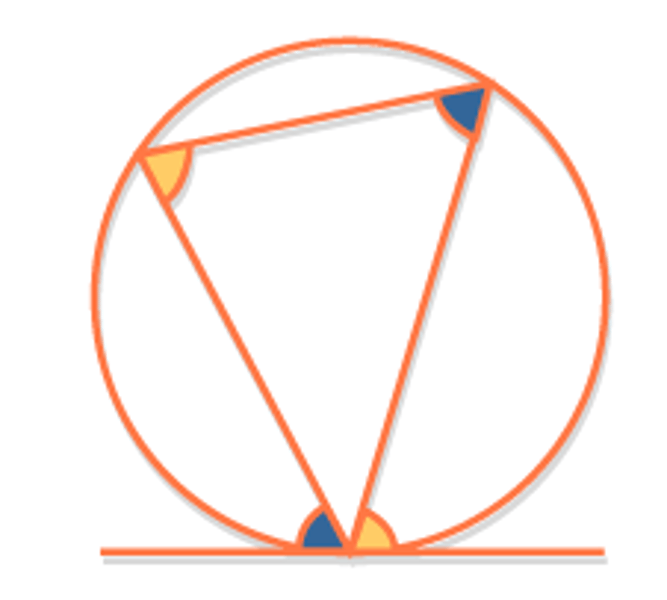
- Alternate segment theorem

Dumb way of remembering them

RACCROBATS:

R - two Radii form an isosceles

A - Angle in a semicircle is 90 degrees

CC - angle at the Centre is twice that at the Circumference

R - Radius and a tangent meet at 90 degrees

O - Opposite angles in a cyclic quadrilateral add up to 180 degrees

B - perpendicular Bisector of a chord goes though the centre

A - Alternate segment theorem

T - Tangents from the same point are the same length

SS - angles in the Same Segment are equal

Alternate segment theorem

Congruent rules in a triangle

- SSS

- AAS

- SAS

- RHS

Similarity rules in a triangle

- All the angles are the same

- All three sides are proportional

- Any two sides are proportional and the angle between them is the same

Translations

This is written as a vector in the form

( x )

( y )

Where x means along the x-axis and y along the y-axis

Rotations

To describe a rotation you need three things:

- The angle of rotation

- The direction of rotation

- The centre of rotation

Reflections

To describe this you need to give the equation of the line it is reflected on.

An invariant point is one that doesn't change, for example on one the mirror line.

Enlargements

To describe an enlargement, you need:

- A scale factor

- A centre of enlargement

Scale factors

- If the scale factor is bigger than one, the shape gets bigger

- If the scale factor is smaller than one (but more than zero), the shape gets smaller

- If the scale factor is negative then it goes then the shape comes out of the other side of the centre of enlargement

- The factor given is relative distance from the centre of enlargement

Area of a triangle

0.5 × base × height

Area of a parallelogram

base × vertical height

Area of a trapezium

0.5 × (a + b) × height

Where a and b are the top and bottom lengths

Area of a rectangle

length × width

Area of a circle

πr²

Circumference of a circle

πd, 2πr

Volume of a cuboid

length × width × height

Volume of a prism

cross sectional area (triangle area) × length

Volume of a cyclinder

πr²h

Volume of a pyramid

1/3 × area of base × height

Area of a sector (of a circle)

x/360 × area of the cull circle

Where x is the angle

Length of an arc (of a circle)

x/360 × circumference of full circle

Volume of frsutrum

Volume of original cone - volume of removed cone

Scale factors with enlargements in other dimensions

For a scale factor n:

- The sides are n times bigger

- The areas are n² times bigger

- The volumes are n³ times bigger

Locus definition

A line or region which satisfies all the points which fit a given rule

Bearings

In order to describe a bearing you need:

- Where you are coming from

- A north line

- The angle clockwise from the north line

Pythagoras theorem

a² + b² = c²