biology 2600 (ecology) - unit 10 (population growth)

Given suitable conditions, aquatic and terrestrial populations have great capacity for growth. How have aquatic populations demonstrated such growth?

- Planktonic populations of diatoms (photosynthetic algae) "bloom" each spring

- Zooplankton populations then increase as they feed on diatoms

What are the similarities between geometric and exponential population growth?

In the presence of abundant resources, populations can grow at geometric or exponential rates; neither of these types of growth can continue indefinitely

A population growing at its maximum rate grows slowly at first:

- Growth then accelerates

- This growth may be geometric or exponential

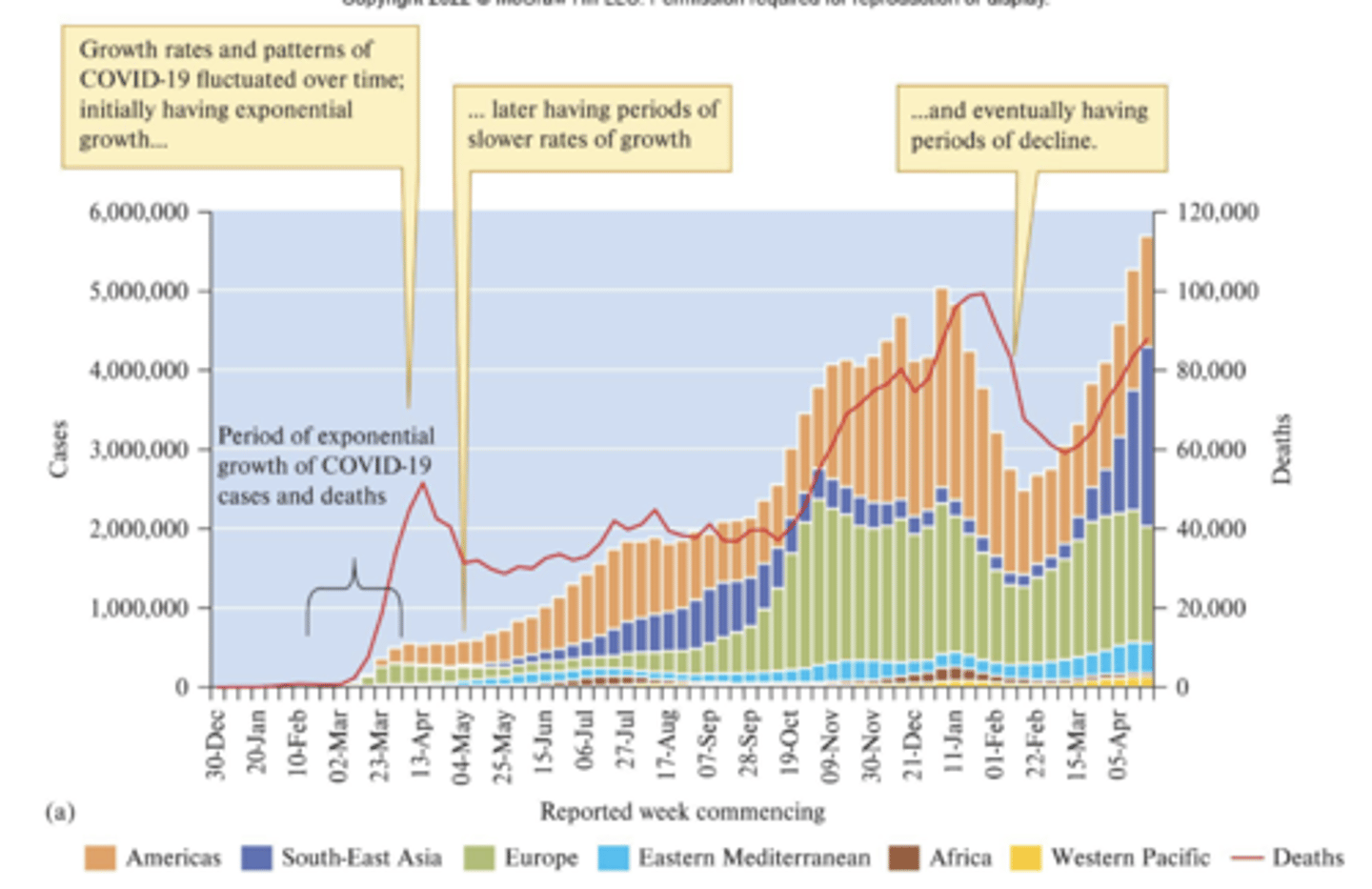
When generations do not overlap, growth can be modelled geometrically (successive generations differ in size by a constant ratio).

How can we calculate geometric growth?

Number of individuals at time t = (initial number of individuals) x (geometric rate of increase) to the power of (number of time intervals or generations)

- Geometric rate of increase: Nt + 1 / Nt

- When rate of increase is 1, population is constant. 0.5 = decreases by half each year. 2 = doubles each year

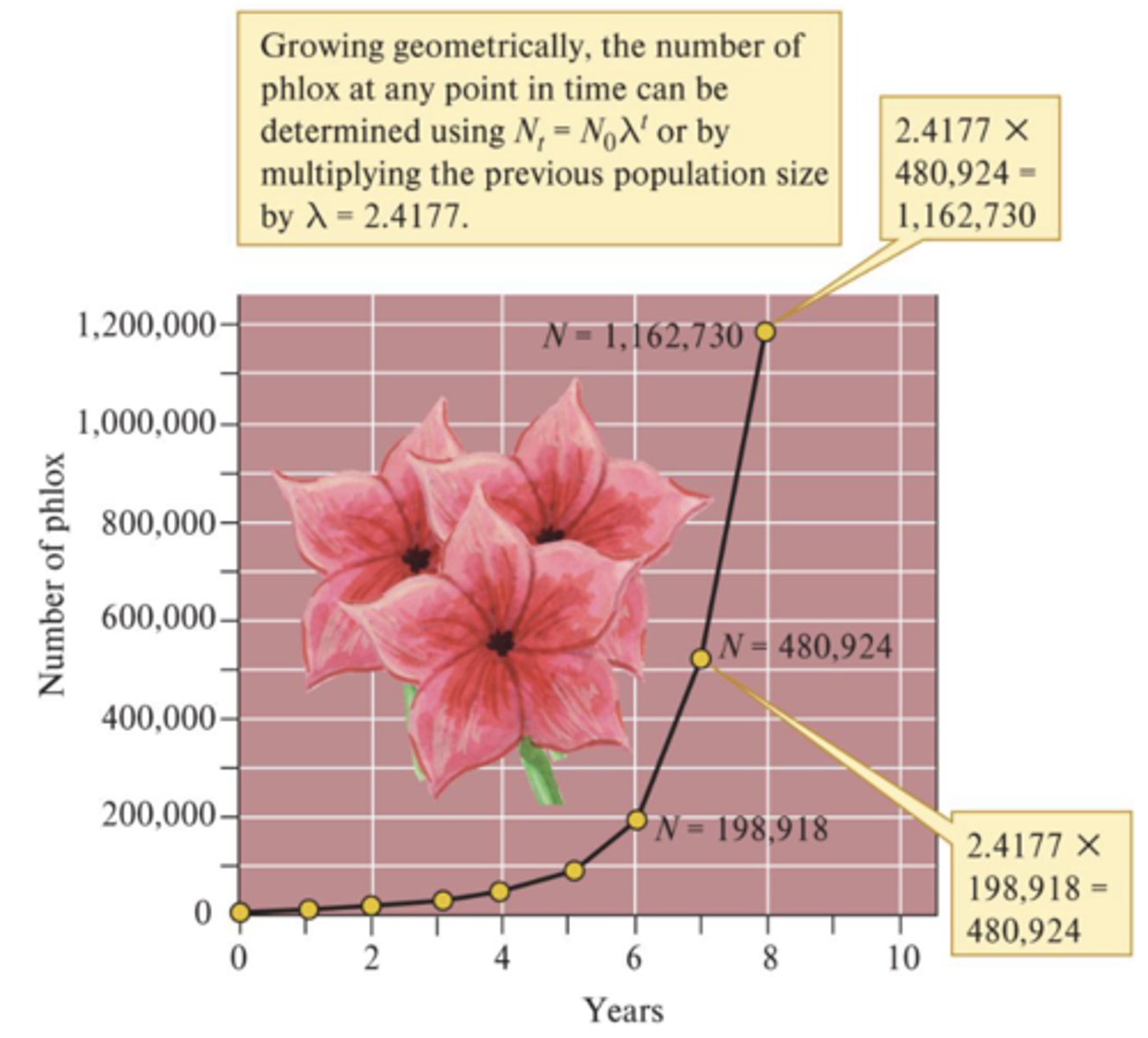
Continuous population growth in an unlimited environment can be modelled exponentially (appropriate for populations with overlapping generations).

How can we calculate exponential growth?

dN/dt = rN. As population size (N) increases, rate of population increase (dN/dt) gets larger

Integrating both sizes of the equation allows us to calculate the number of individuals at a certain time. This is determined by the initial number of individuals, the per capita rate of increase, and the number of time intervals

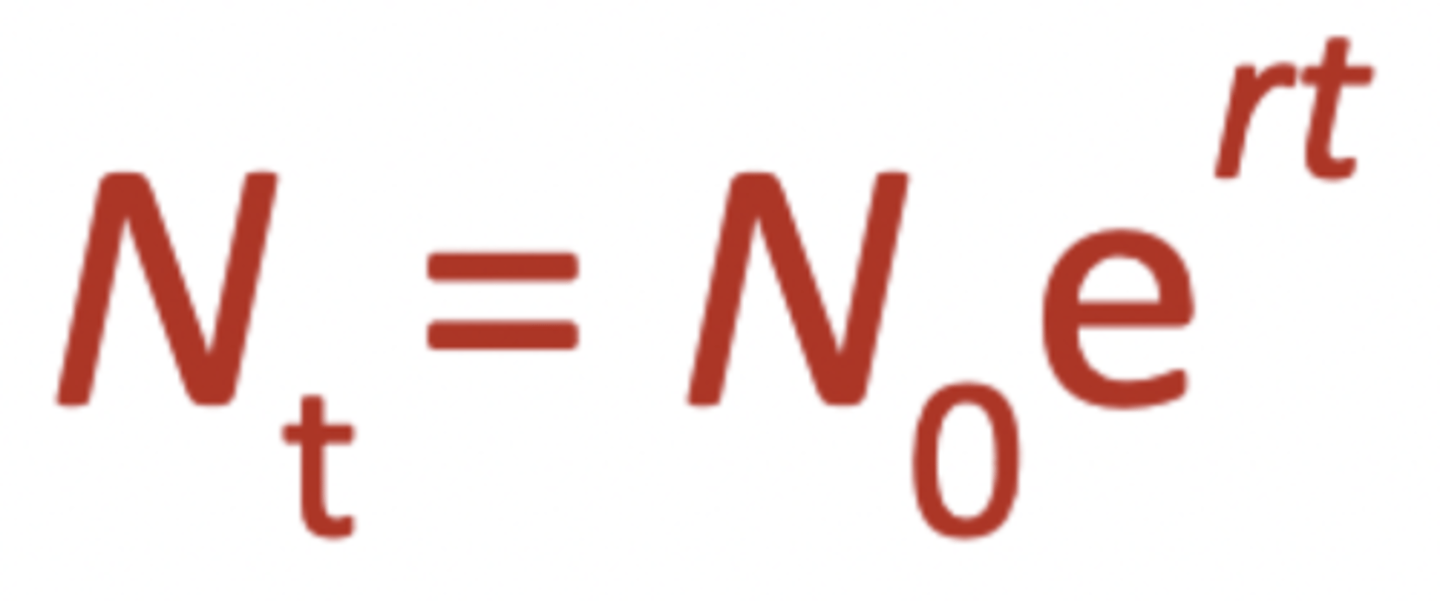
Under what conditions is exponential growth in nature observed (i.e. postglacial tree populations in Britain)?

Assumption of constant rate of per capita increase may seem unrealistic. Natural populations may grow exponentially for short periods of time if abundant resources are present

- Pollen records document growth of postglacial tree populations in Britain

- Exponential growth for 400-500 years

What is the first stage of exponential growth?

Begin growth in favourable environments at low densities:

- Planktonic diatoms (i.e. algal blooms), whooping cranes

- Whooping cranes reduced to 22 in 1940

- Grew exponentially to 220 in 2005

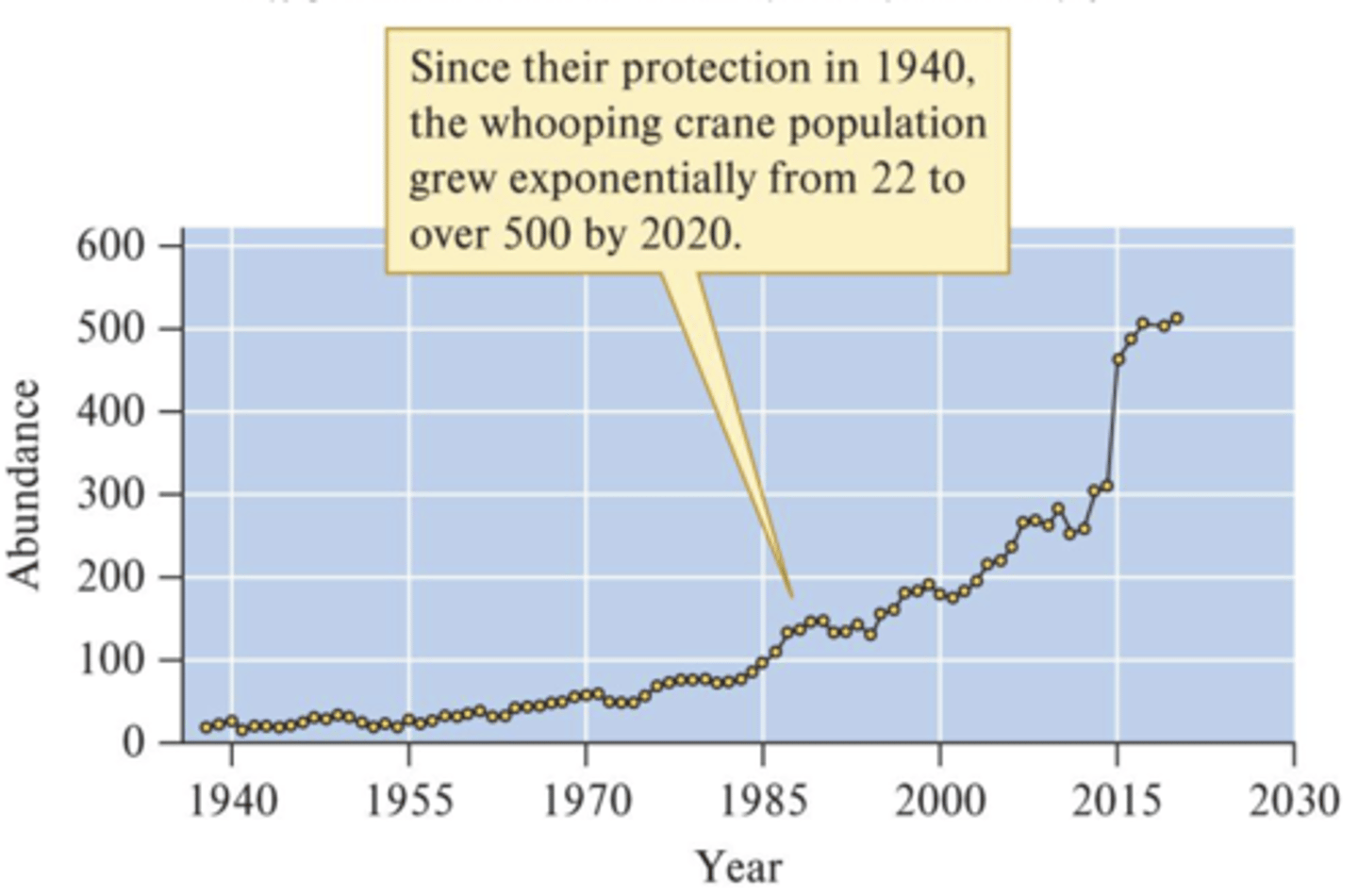
Why is exponential growth important?

May be important during establishment in new environments, during temporary favourable conditions, and during recovery from exploitation

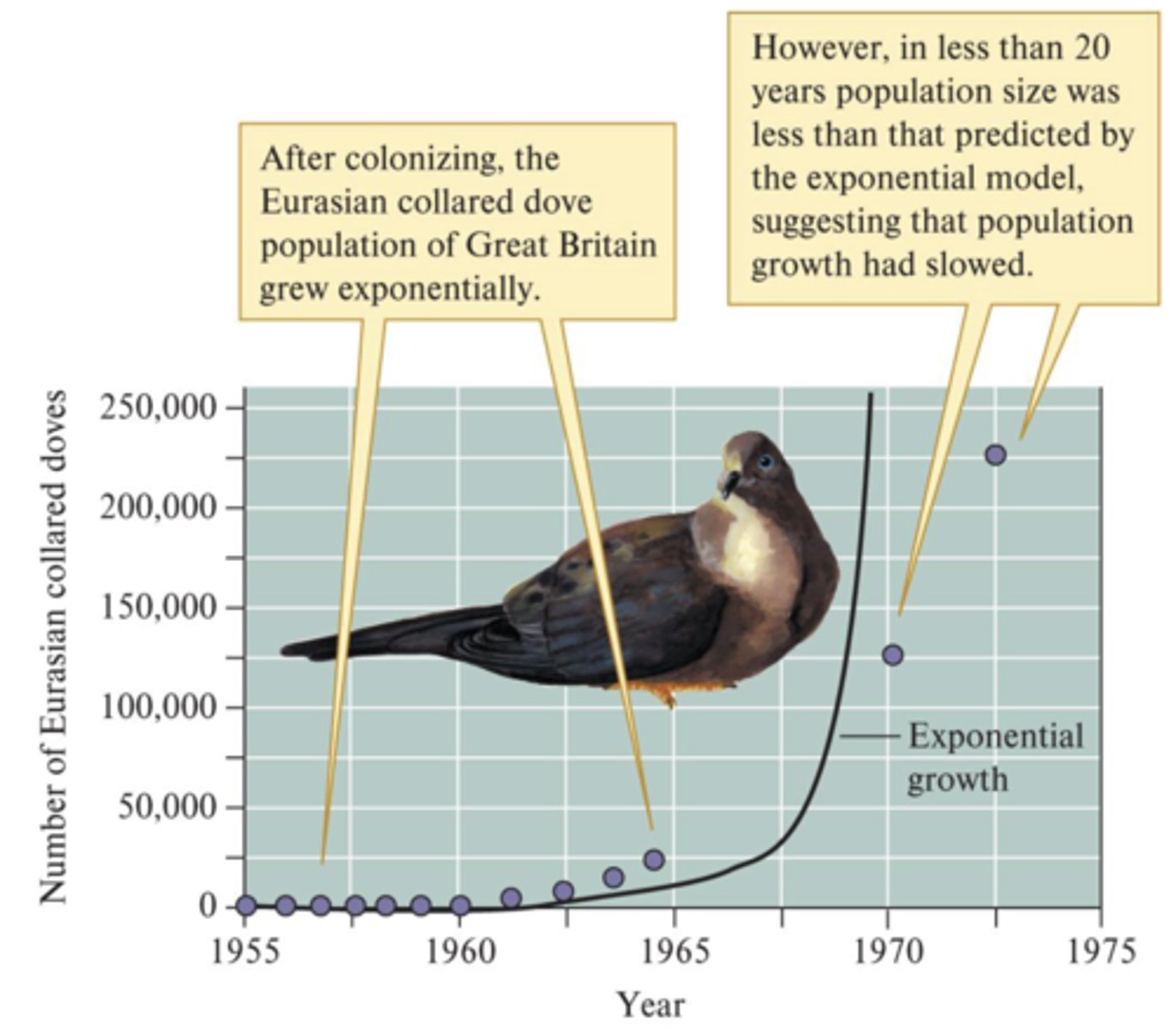
What is the second stage of exponential growth?

Eurasian collared dove expanded into Western Europe in the 20th century. Population grew exponentially for a decade or more, then rate of population growth began to slow

- Suggests that population was approaching environmental limits (i.e. running out of resources, nesting sites)

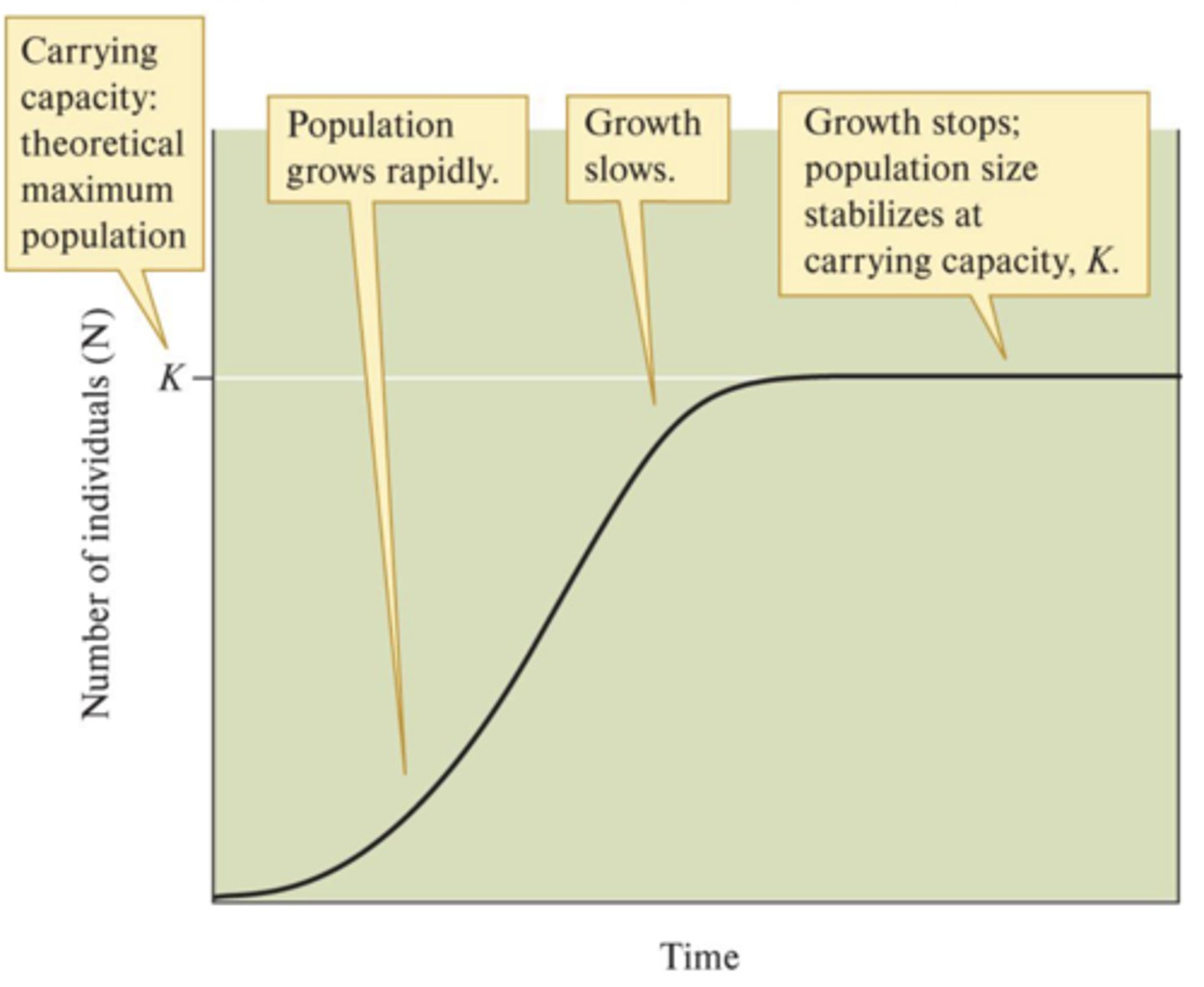
Logistic Population Growth

As resources are depleted, population growth rate slows and eventually stops (exponential growth cannot continue). Growth rate slows, then population size levels off (sigmoidal population growth curve)

Finite amount of resources can only support a finite number of individuals

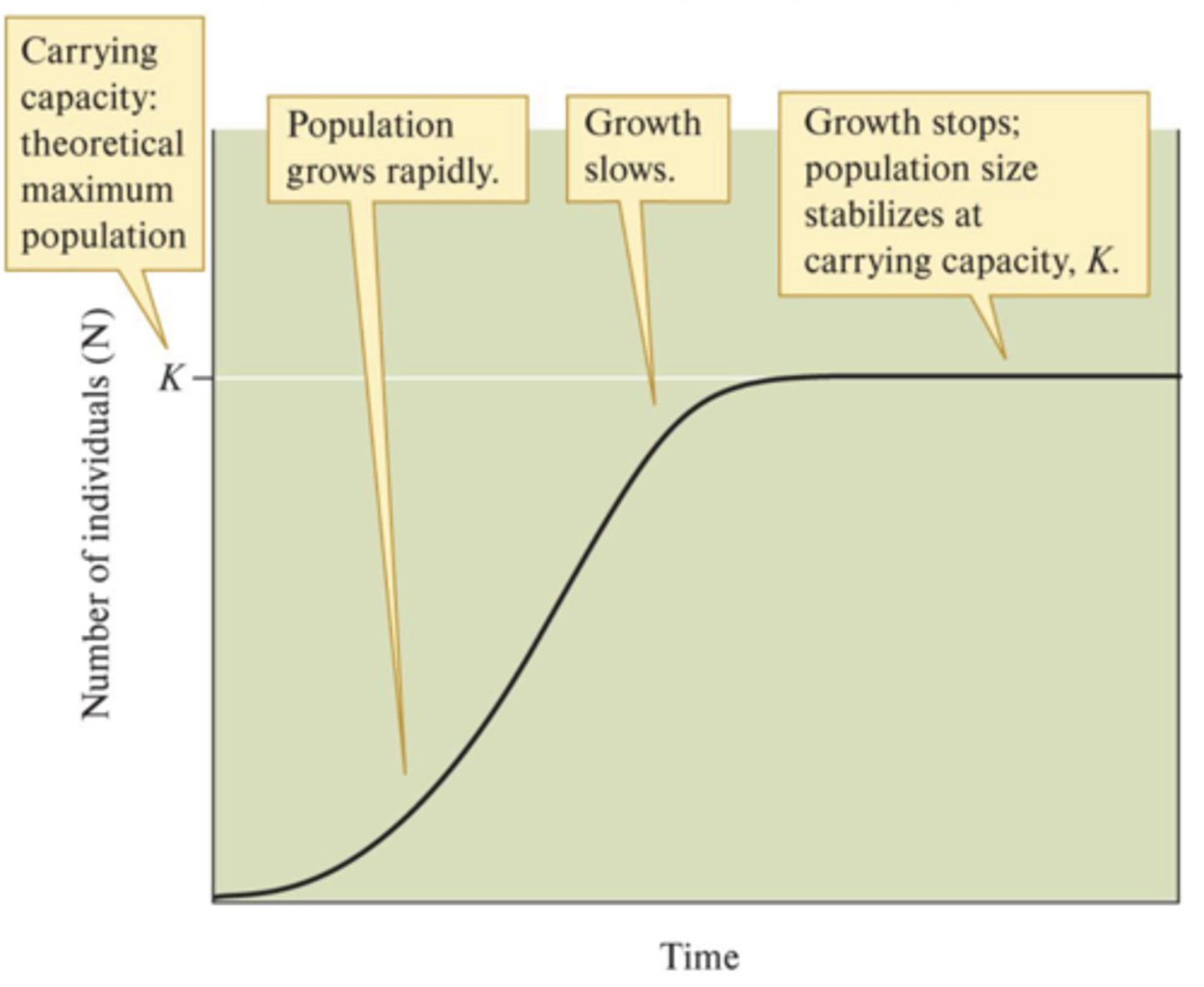
Carrying Capacity (K)

Population size that a particular environment can support (demonstrated in logistic population growth)

Logistic growth rate (slope) is the highest when N = K/2. Why not when N is close to 0? Why not when N is close to K?

- When N is close to 0, there are abundant resources and slow initial growth

- As N approaches K, the fraction of unused resources becomes very small, approaching 0. Resources become limiting, and population begins to level off

- At N = K/2, population is large enough to have a high number of reproductive individuals, but there are still substantial unused resources to allow for rapid expansion

The logistic growth formula is derived from the modification of the exponential growth formula.

How can we calculate logistic population growth?

- Exponential growth with the "braking" term that slows the growth; the higher the population size is, the more "braking"

- As population size increases, logistic growth rate becomes a small fraction of the growth rate (i.e. growth slows)

When N = K, population growth ceases. What happens when N overshoots K?

The environment can no longer support the population size, and the population declines (negative growth rate)

Density-Dependent Factors

- Affected by population density

- Often are biotic factors

- Disease, competition, predation

Environment influences population growth by affecting birth and death rates

Density-Independent Factors

- Not affected by population density

- Often are abiotic factors

- Floods, extreme temps