Damped Oscillation [Part-II]

b^2 < 4mk

(1)

b^2 = 4mk

(2)

b^2 > 4mk

(3)

The term ((k/m) - (b/(2m))^2) becomes negative, making the angular frequency imaginary, which means no oscillations occur. The system only decays exponentially toward rest.

What happens when the damping constant becomes very large?

Because damping opposes motion. If it’s too strong, it slows the system so much that it cannot oscillate, it will just slowly move toward equilibrium instead of swinging back and forth.

Why must damping be small for oscillations to occur?

angular frequency, ((k/m) - (b/(2m))^2)^1/2

As the damping increases, the _________________,decreases since damping weakens the effective restoring force. The motion becomes slower as b increases in……………

The damping constant must be less than the critical value

What condition must be met for a system to oscillate?

b < (4mk)^1/2

Mathematical representation of the damping value being less than the critical value.

((k/m) - (b/(2m))^2)^1/2

Formula for the angular frequency in a damped oscillator

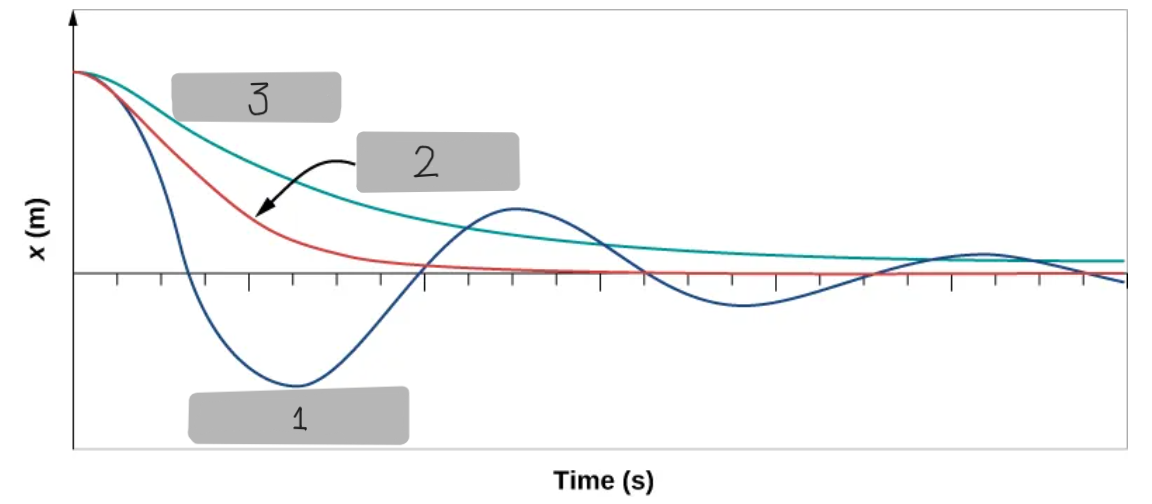
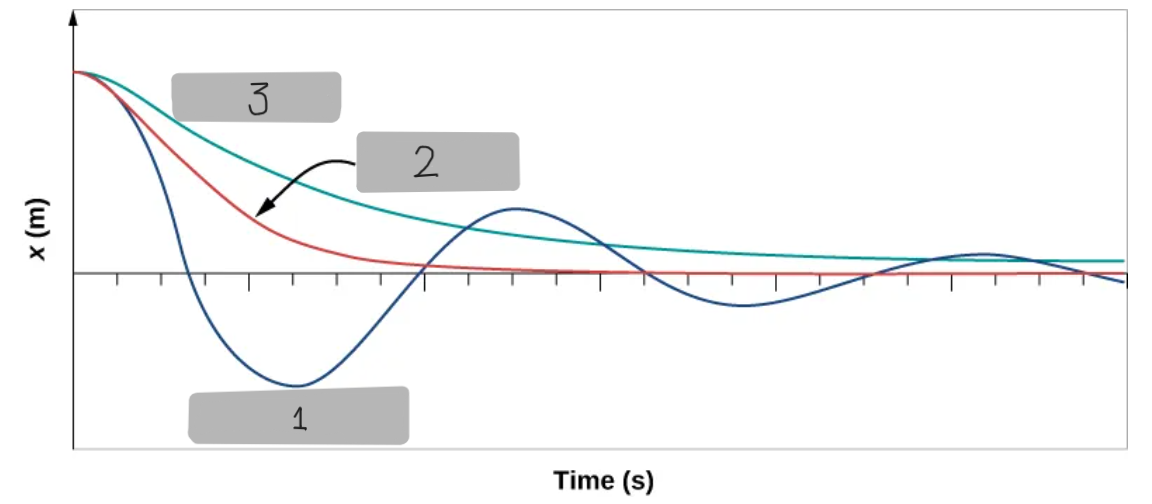
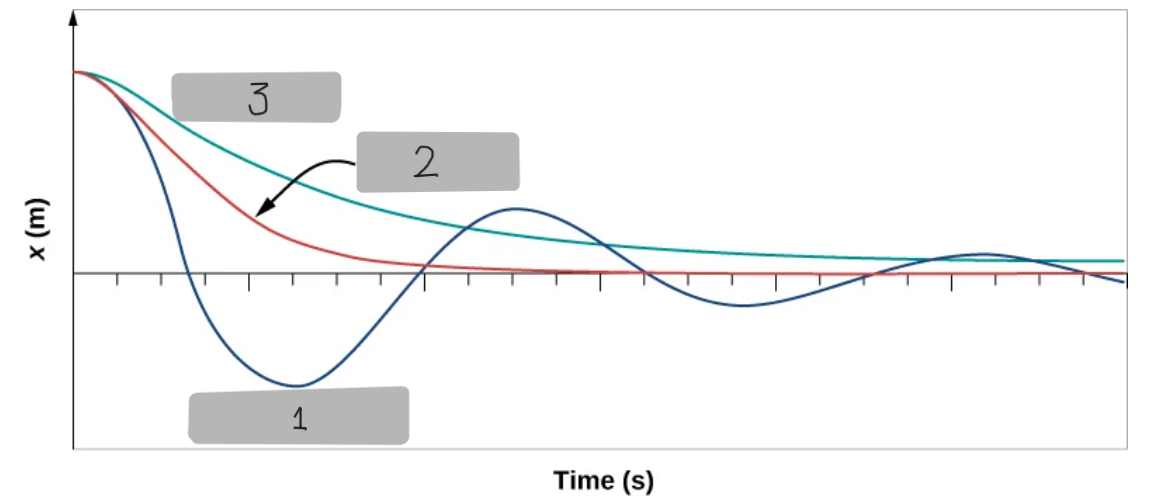
Underdamped Motion

• When damping is small

• b < (4mk)^1/2

• the system oscillates with gradually decreasing amplitude

• Most real systems, such as a mass on a spring in air, follow this motion

Critically Damped Motion

• Occurs when b = (4mk)^1/2

• The system returns to equilibrium as quickly as possible without oscillating

• This is desirable in systems like shock absorbers in vehicles

Overdamped Motion

• Occurs when b > (4mk)^1/2

• The system does not oscillate and returns to equilibrium slowly,

• taking longer than in the critically damped case.