Week 5: Pearson's Chi Square

Pearson’s chi square

-relationship between variables

• IV → categorical

• DV → categorical

-there is no non-parametric version

characteristics of chi square test

• only uses categorical variables

• variables are measured as frequency

• makes inferences about likelihood

• numbers in each cell should be independent

inferences about likelihood (characteristics)

-it matters whether you are part of one specific category in the first variable for how it affects your likelihood to be part of a specific category in the second variable

numbers in each cell should be independent (characteristics)

-one observation/participant can only be in one cell

-categories should be mutually exclusive

frequency table

-called crosstabs in SPSS

-shows us the frequency of observations or participants that belong in each cell

p value

-probability of finding a relationship in the sample if there is no relationship in the population

chi square analysis

-compare the observed values in the sample to the expected values if there was no relationship between the variables → if the values were equally divided amongst the cells in the table

observed values

-what actually happens in the sample

expected values

-the values we would expect if the null hypothesis is true

are the differences between observed and expected values significant?

-use Pearson’s Chi Square Test

-compares observed values from within the sample to our expected values

null hypothesis testing (chi square)

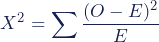
-for each cell, calculate the difference between observed values (O) and expected values (E)

-the bigger the difference is between the expected and observed values → the larger the chi square value will be

-the larger the chi square value is, the more likely it is that you can reject the null hypothesis

count (results table)

-observed values

expected count (results table)

-expected values

assumptions to use Pearson’s Chi Square

• no more than 25% of the cells should have expected value less than 5

• no individual cell should have expected value less than one

-if these assumptions are not met → report Fisher’s Exact test results → but only for 2×2 test

interpreting Chi Square test

-does not say anything about the direction of the relationship → can only conclude that there is a relationship

-bar graph and descriptive statistics can give you an idea of the direction of the relationship

degrees of freedom

-within Chi Square test we do not calculate the degrees of freedom based on the number of people in our sample

-do it on the basis of the number of categories within each variable

-calculated by taking the number of categories within one variable and subtracting one from that

-then do the same with the number of categories on the other variable

degrees of freedom equation

(number of rows - 1) x (number of rows - 1)

descriptive statistics (reporting results)

-specify which variables we compared

-overview of percentages, appropriate for the research question

inferential statistics (reporting results)

-relationship significant or not

-x²(df, N = [sample size]) = [x² value], p = [p value]

interpretation of results (reporting results)

-make sure to link it back to the terms in the research question

Cramer’s V

-measure of effect for the Chi Square test

interpretation of Cramer’s V value

• less than 0.10 = trivial effect

• 0.10 - 0.30 = small effect

• 0.30 - 0.50 = medium effect

• more than 0.50 = large effect

-larger the value, indicated more important/pronounced relationship

shared variance of Cramer’s V

-calculate the shared variance by squaring the Cramer’s V value