PSY2750 Quiz 1

Summation notation (∑)

Total sum of values

∑X² vs (∑X)²

Because squaring is applied before summation in ∑X²

Nominal scale measurement

Blood type (A, B, O)

Scale of measurement with true zero

Ratio

Experimental vs non-experimental study

Experimental studies manipulate variables; non-experimental studies do not

Population parameter notation

μ (population mean)

Purpose of a frequency distribution

To organize data into categories with corresponding frequencies

Formula for the sum of frequencies

N = ∑fX

Graphical representation for continuous data

Histogram

Cumulative frequency

A running total of frequencies up to a certain point

Measure of central tendency affected by extreme values

Mean

Best measure of central tendency for ordinal data

Median

Variability in a data distribution

The differences between scores and how spread out they are

Formula for the range in a dataset

Xmax - Xmin

Standard deviation measures

How scores are distributed around the mean

Difference between variance and standard deviation

Variance is the square of the standard deviation

What a z-score represents

The distance of a score from the mean in standard deviation units

z-score for X = 90 with mean 80 and SD 5

2.0

True about z-scores

The shape of the z-score distribution is the same as the original distribution

Meaning of a z-score of -2.00

The score is 2 standard deviations below the mean

σ

population standard deviation

s

sample standard deviation

∑

summation (sum of all numbers)

N

population (total number)

n-1

sample (total number)

SS

sum of squares

formula:

- find deviations (X - μ)

- square

- sum them up

ex. Data: 2, 4, 6

1. Mean: μ= 2 + 4 + 6 / 3 = 4

2. Find each deviation from the mean: (2−4),(4−4),(6−4) = −2, 0, 2

3. Square each deviation: (−2)^2, (0)^2, (2)^2 = 4, 0, 4

4. Sum the squared deviations: 4+0+4=8

So, SS = 8

SS formula

SS=∑X^2−(∑X)^2/N

ex. ∑X = 1 + 3 + 5 = 9

∑X² = 1² + 3² + 5² = 1 + 9 + 25 = 35

SS = 35 - 27 = 8

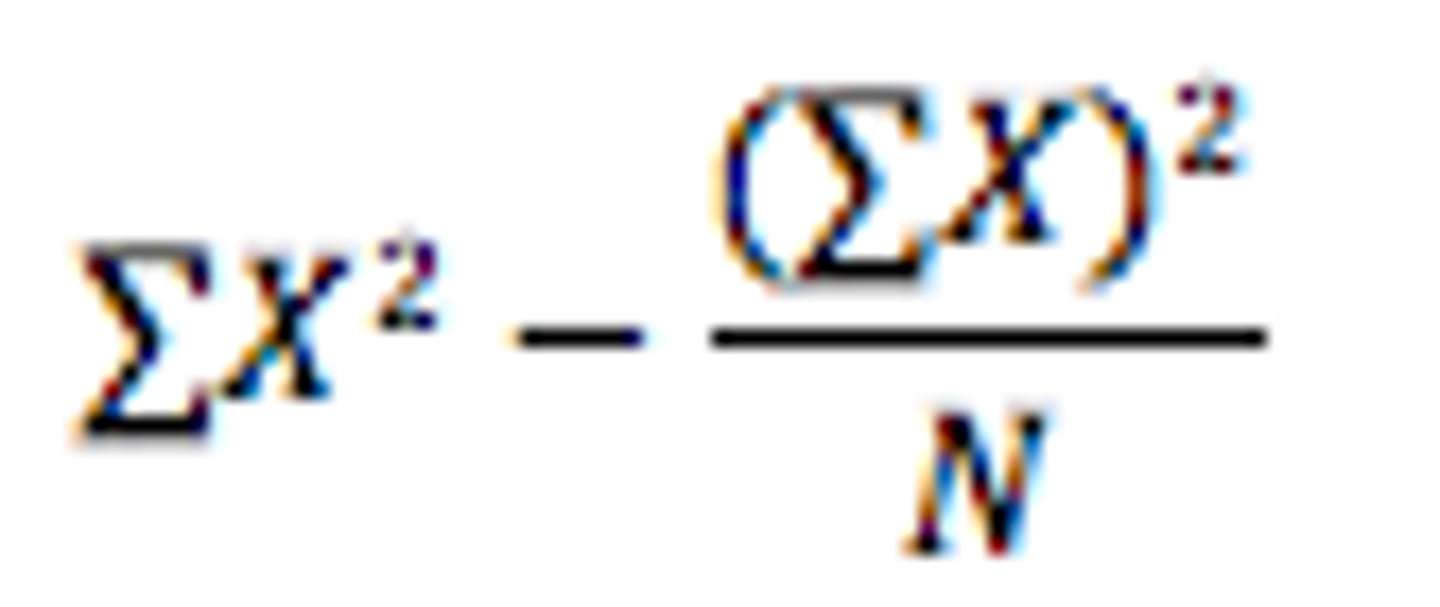
weighted mean

- accounts for the contribution of different sample sizes

- calculates the overall mean by summing the values from different groups and dividing by the total number of observations

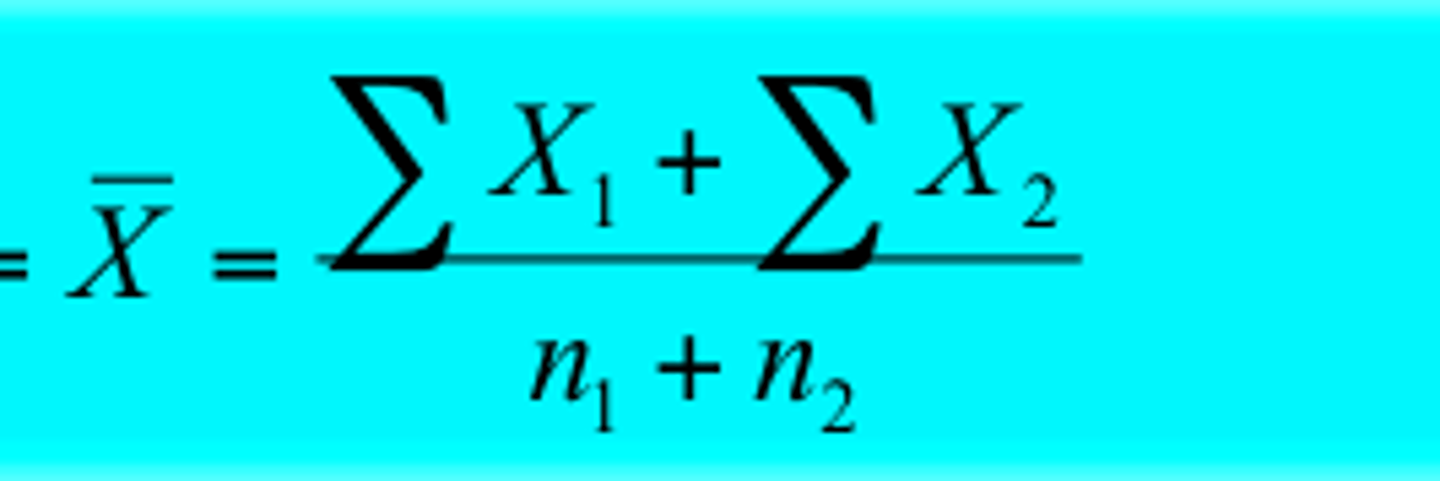
σ²

population variance

s²

sample variance

variance

squared measure of spread

standard deviation

- measures the average distance of data points from the mean

- square root of variance

Z-score

- represented by 'z'

- measures how many standard deviations a data point is from the mean

- positive Z-score = value is above the mean

- negative Z-score = value below the mean

ex. Z-score of 2 means the value is 2 standard deviations above the mean.

μ

mean of population

Z-score formula

z = (X- μ)/σ

z=(x-mean)/standard deviation

M

mean of sample

descriptive statistics

summarizing data from one group with one or more variables

correlational methods

examining the relationship between two variables in one group

comparative methods

comparing two or more groups across one or more variables

experimental methods

manipulating variables to establish cause-and-effect relationships between them

non-experimental methods

observing relationship between variables without manipulation

frequency distribution

a way to organize and summarize data by grouping it into categories or intervals and showing how often each category or interval occurs

frequencies

number of times a value or range of values appears in the dataset

class interval

a range of values used to group data in a frequency distribution

histogram

used for continuous data

smooth curve

used for large datasets

bar graph

used for categorical data

cumulative frequency

add each frequency to the sum of previous frequencies