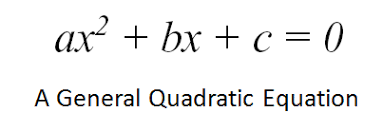B1 Dual Credit College Algebra

Quadratic Formula

The Quadratic Formula is used to find the solutions to a quadratic equation in the form ax² + bx + c = 0. It is expressed as x = (-b ± √(b² - 4ac)) / (2a).

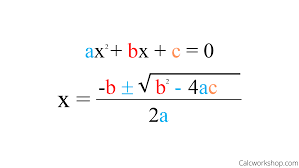
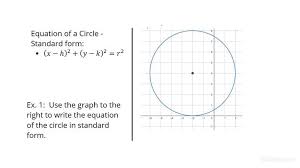
Standard Form Equation of a Circle

An equation that represents a circle in the Cartesian plane, expressed as (x - h)² + (y - k)² = r², where (h, k) is the center and r is the radius.

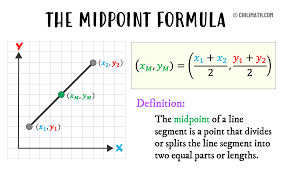
Midpoint

The Midpoint of a line segment is the point that divides the segment into two equal parts, calculated as M = ((x₁ + x₂)/2, (y₁ + y₂)/2) for endpoints (x₁, y₁) and (x₂, y₂).

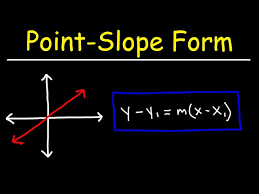
Point-Slope Equation of a Line

An equation that expresses the relationship between the coordinates of a point on a line and its slope, typically written as y - y₁ = m(x - x₁), where m is the slope and (x₁, y₁) is a point on the line.

Distance Formula

The Distance Formula calculates the length between two points in the Cartesian plane, given as d = √((x₂ - x₁)² + (y₂ - y₁)²), where (x₁, y₁) and (x₂, y₂) are the coordinates of the points.

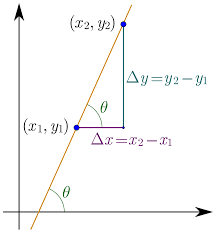
Slope

The Slope of a line is a measure of its steepness, calculated as the ratio of the vertical change to the horizontal change between two points on the line, represented as m = (y₂ - y₁) / (x₂ - x₁).

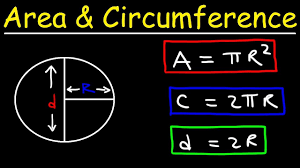
Circumference and Area of a Circle

The Circumference and Area of a Circle are calculated using the formulas C = 2πr and A = πr², where r is the radius of the circle. These formulas relate the distance around the circle to its size.

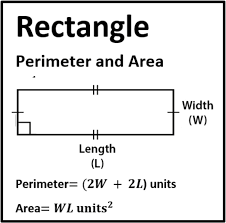
Perimeter and Area of a Rectangle

The Perimeter and Area of a Rectangle are calculated using the formulas P = 2(l + w) and A = lw, where l is the length and w is the width of the rectangle.

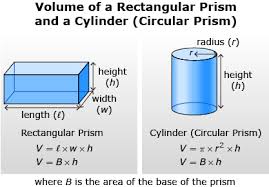
Volume of Cylinder and Rectangular Prism

The Volume of a Cylinder and Rectangular Prism are calculated using the formulas V = πr²h for cylinders and V = lwh for rectangular prisms, where r is the radius, h is the height, l is the length, and w is the width.

Average Rate of Change

The Average Rate of Change is a measure of how a quantity changes over an interval, calculated as the change in the quantity divided by the change in the independent variable. It can be represented as ( \frac{f(b) - f(a)}{b - a} ) for a function ( f ) over the interval ( [a, b] ).

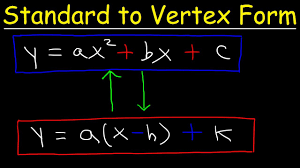
Standard (Vertex) Form Equation of Quadratic

The Standard (Vertex) Form Equation of a Quadratic is represented as y = a(x - h)² + k, where (h, k) is the vertex of the parabola, and a determines the direction and width of the parabola.

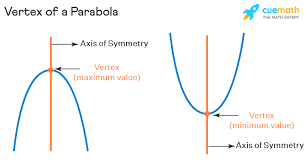
Vertex of a Parabola

The point on a parabola where it changes direction, represented as (h, k) in the standard form equation.

Even and Odd Function Test

The Even and Odd Function Test determines the symmetry of a function. A function is even if f(-x) = f(x) for all x, and odd if f(-x) = -f(x) for all x.

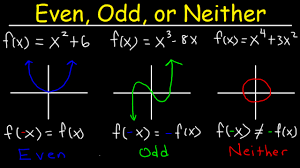
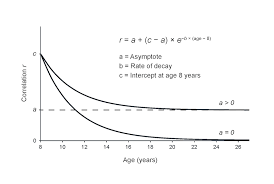
Continuous Rate of Decay Model

A model that describes the decrease of a quantity at a rate proportional to its current value, represented by the formula A = A0 e^{-kt}, where A0 is the initial amount, k is the decay constant, and t is time.

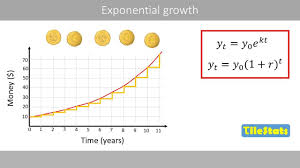
Continuous Rate of Growth Model

A model that describes the increase of a quantity at a rate proportional to its current value, represented by the formula A = A0 e^{kt}, where A0 is the initial amount, k is the growth constant, and t is time.

Product Property of Logs

The Product Property of Logs states that the logarithm of a product is equal to the sum of the logarithms of its factors. In mathematical terms, ( \logb(MN) = \logb(M) + \log_b(N) ).

Quotient Property of Logs

The Quotient Property of Logs states that the logarithm of a quotient is equal to the difference of the logarithms of the numerator and denominator. In mathematical terms, ( \logb\left(\frac{M}{N}\right) = \logb(M) - \log_b(N) ).

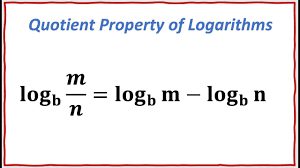
Power Property of Logs

The Power Property of Logs states that the logarithm of a number raised to an exponent is equal to the exponent times the logarithm of the number. In mathematical terms, ( \logb(M^p) = p \cdot \logb(M) ).

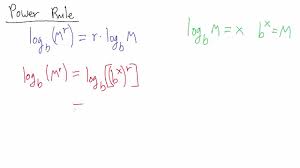
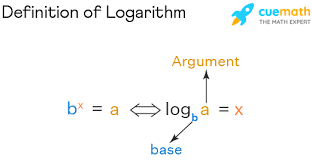
Logarithm Definition

A logarithm is the power to which a number must be raised in order to get some other number (see Section 3 of this Math Review for more about exponents). For example, the base ten logarithm of 100 is 2, because ten raised to the power of two is 100: log 100 = 2.

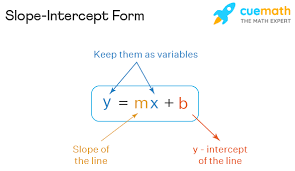
Slope-Intercept Equation of Line

The slope-intercept form is simply the way of writing the equation of a line so that the slope (steepness) and y-intercept (where the line crosses the vertical y-axis) are immediately apparent.

General Form Equation of Quadratic

In math, we define a quadratic equation as an equation of degree 2, meaning that the highest exponent of this function is 2. The standard form of a quadratic is y = ax^2 + bx + c, where a, b, and c are numbers and a cannot be 0. Examples of quadratic equations include all of these: y = x^2 + 3x + 1. y = x^2.