ch8 capacitance L11

surface of a conductor must be equipotential because

positive and negative charges move to cancel out any differences in potential until they are equal

E-field visualized with field lines, so electric potential visualized with

equipotential surface

equipotential surface formed by

the locus of points all of which have the same potential i.e. moving test charge from A to infinity or B to infinity involves the same amount of work

equipotential lines are drawn by

making them perpendicular to E-field lines

if we know V, we can get equipotential surface by

equating V to k q/r, flipping around and solving for r

moving charge from any point on an equipotential surface to another point on same surface involves

zero work

surface of conductors must be equipotential because

any voltage difference would disappear, with + charges moving to lower voltage and - charges moving to higher voltage

if two conducting spheres connected by wire, they are at

equipotential

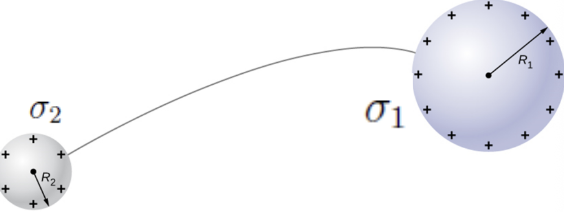
since the two spheres are at equipotential,

σ₁R₁ = σ₂R₂

if radius is smaller, the surface charge density is

greater

as more charge is added to conductor, it is

more difficult to keep adding

capacitance

proportional coefficient that relates Q and C

capacitance equation

Q = CV

value of C depends on

shape, size, and medium around the conductor; intrinsic property

unit of C

coulomb/volt = farads (F)

capacitor

device for storing charge, consisting of two conductors separated by some small distance

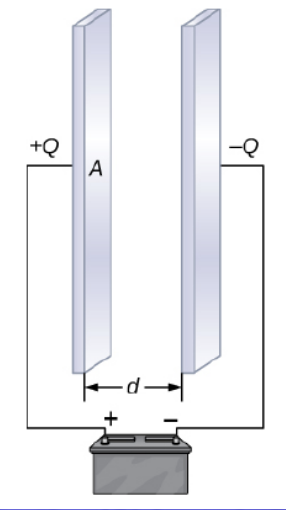
parallel plate capacitance

C = ε₀A/d