Lecture 4: Energy, Linear Momentum, Rotational Motion, Statics

Kinematics

description of motion (how things move)

Dynamics

Causes of motion (why things move)

Strong Nuclear 

One of the four fundamental forces that holds atomic nuclei together, overcoming the repulsive electromagnetic force between protons.

Weak Nuclear 

One of the four fundamental forces that is responsible for radioactive decay and neutrino interactions, playing a crucial role in nuclear reactions.

Electromagnetic

One of the four fundamental forces that gives matter stability, rigidity, etc., and gives em radiation

Gravitation

One of the four fundamental forces that governs large scale structure of the universe, gives orbits, etc.

Is it easy to understand how things behave from the fundamentals?

no

Would a rocket moving upward slow down or speed up (assuming it uses no further propulsion)

slow down

What would happen if a rocket would slow down to a stop before it reaches it’s destination?

It would be dangerous, only safe when it reaches to its destination

Energy

abstract concept; important because it’s conserved (can figure out how systems behave by balancing it before and after)

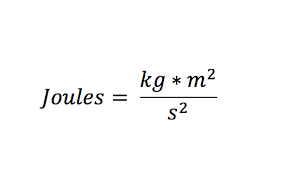
Joule

SI unit of energy

Kinetic energy 

energy due to motion

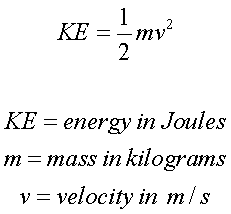
Gravitational Potential Energy (Earth)

energy stored due to an object's height above the ground, calculated as the product of mass, gravity, and height.

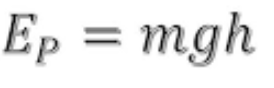
Conservation of Energy

(KE +PE) final = (KE + PE) Initial

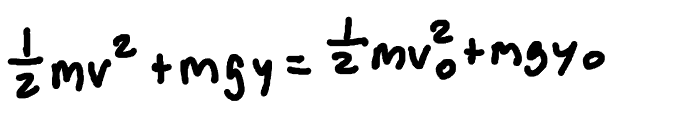
PE between objects of masses m and M (not close to Earth)

The gravitational potential energy between two masses m and M at a distance r apart is given by the formula U = -G(mM/r), where G is the universal gravitational constant.

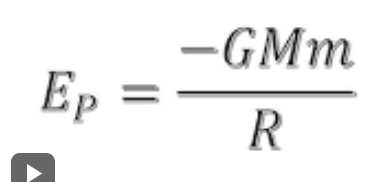
Spring Potential Energy

The energy stored in a compressed or stretched spring, calculated using the formula U = 1/2 kx², where k is the spring constant and x is the displacement from its equilibrium position.

Work

a technical concept, different from the day-to-day sense

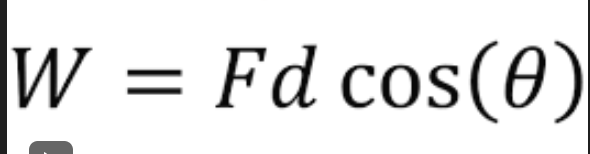
Power

Rate of doing work (unit is Watt (1J/sec); rate of emission or absorption of energy

Momentum

The quantity of motion an object possesses, defined as the product of its mass and velocity (p = mv), and is a vector quantity with both magnitude and direction.

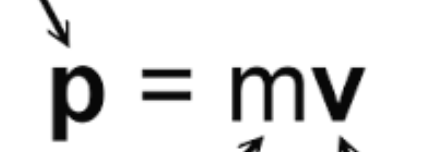
Impulse

A change in momentum resulting from a force applied over time, defined as the product of the force and the time duration during which it is applied (Impulse = Force × Time).

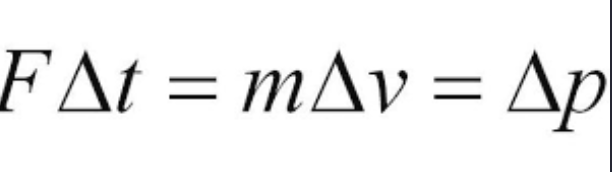
Conservation of Momentum

For an isolated system, momentum cannot change

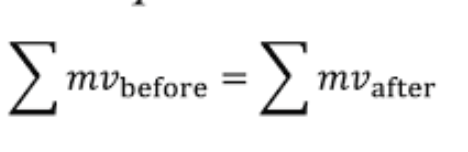
Inelastic collisions

KE is not conserved in the process

Elastic collisions

KE is conserved in the process 

Conservation of Momentum (Elastic)

For elastic collisions, the total momentum and total kinetic energy of the system before and after the collision remain constant.

Conservation of KE + Momentum (Elastic)

In elastic collisions, both kinetic energy and momentum are conserved throughout the process.

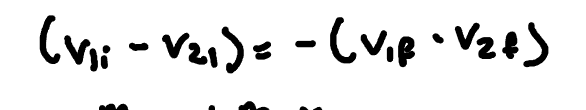
Center of Mass

Captures the concept where the effective mass is

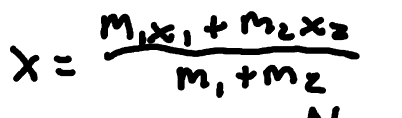
Equilibrium

“staying the same”; not changing 

Static Equilibrium

motionless

Dynamic Equilibrium

Uniform motion (fixed speed and direction)

1st Condition for Equilibrium

For an object to be in equilibrium, the net force acting on it must be zero

2nd Condition for Equilibrium

For an object to be in equilibrium, the net torque acting on it must be zero 

Torque

rotational version of force; a vector that can be clockwise or counterclockwise; greater = “easier” it is to “make rotation”

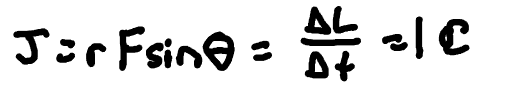
Stable equilibrium

A system is said to be in this type of equilibrium if, when displaced from equilibrium, it experiences a net force or torque in the same direction opposite to the direction of the displacement

Unstable Equilibrium

A system is said to be in this type of equilibrium if, when displaced from equilibrium, it experiences a net force or torque in a direction as the direction as the displacement

Neutral Equilibrium

A system is in this type of equilibrium if its equilibrium is independent of displacements from its original position.

Degrees to radians

is a conversion method used to transform angle measurements from degrees to radians, where one full circle is equal to 360 degrees or 2π radians.

Radians

unitless; ratios of lengths

arc length formula 

s = rθ, where s is the arc length, r is the radius, and θ is the angle in radians.

displacement (rotational motion)

the change in position of an object in a rotational motion, measured as the angle through which the object has rotated.

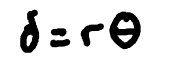
speed/ velocity (rotational motion)

the rate of change of angular displacement of an object; it describes how fast an object rotates around an axis.

Tangential Acceleration

The rate of change of tangential velocity of an object in rotational motion, defined as the linear acceleration along the path of motion.

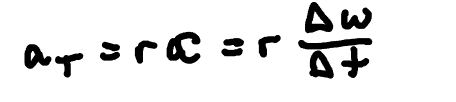
Centripetal Acceleration

the acceleration directed toward the center of a circular path, which keeps an object moving along that path.

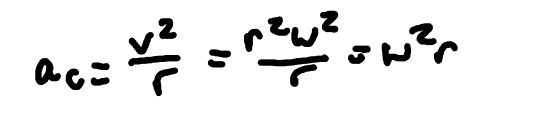
Difference between centripetal acceleration and angular/rotational acceleration

Angular/rotational acceleration is tangent to the direction of motion while centripetal acceleration is radial

Frequency of rotational motion

measured in rev/sec (Hz)

Period of rotational motion

time for one revolution

Kinematic Equation A (Rotational Motion)

Kinematic Equation B (Rotational Motion)

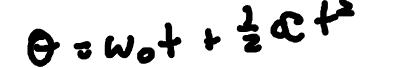
Kinematic Equation C (Rotational Motion)

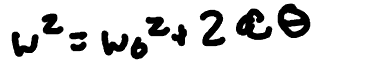
Moment of Inertia 

Rotational version of mass. It is calculated with respect to the axis around which the rotation occurs; measure of a body’s resistance to torque

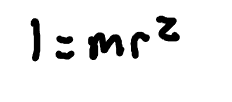
Moment of Inertia Decreases when..

mass is concentrated further from the axis (at larger values of r) 

Total KE of a moving object

sum of linear and rotational KE

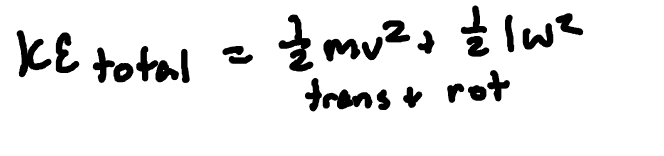
Angular Momentum

the product of an object's moment of inertia and its angular velocity. It represents the rotational analog of linear momentum.