Logic in Modern Mathematics: Propositions, Connectives, and Truth Tables

Logic

science of reasoning

Proposition

(statement) assertion that is true or false, but never both.

Simple proposition

single statement which does not contain other statements as parts.

Compound proposition

contains two or more statements.

Conditional Statement

"If p then q" is a statement called implication, or conditional statement.

Hypothesis

p is hypothesis, premise or antecedent

Conclusion

q is conclusion or consequence

Converse

implicational statement which is the result of reversing its two constituent statements.

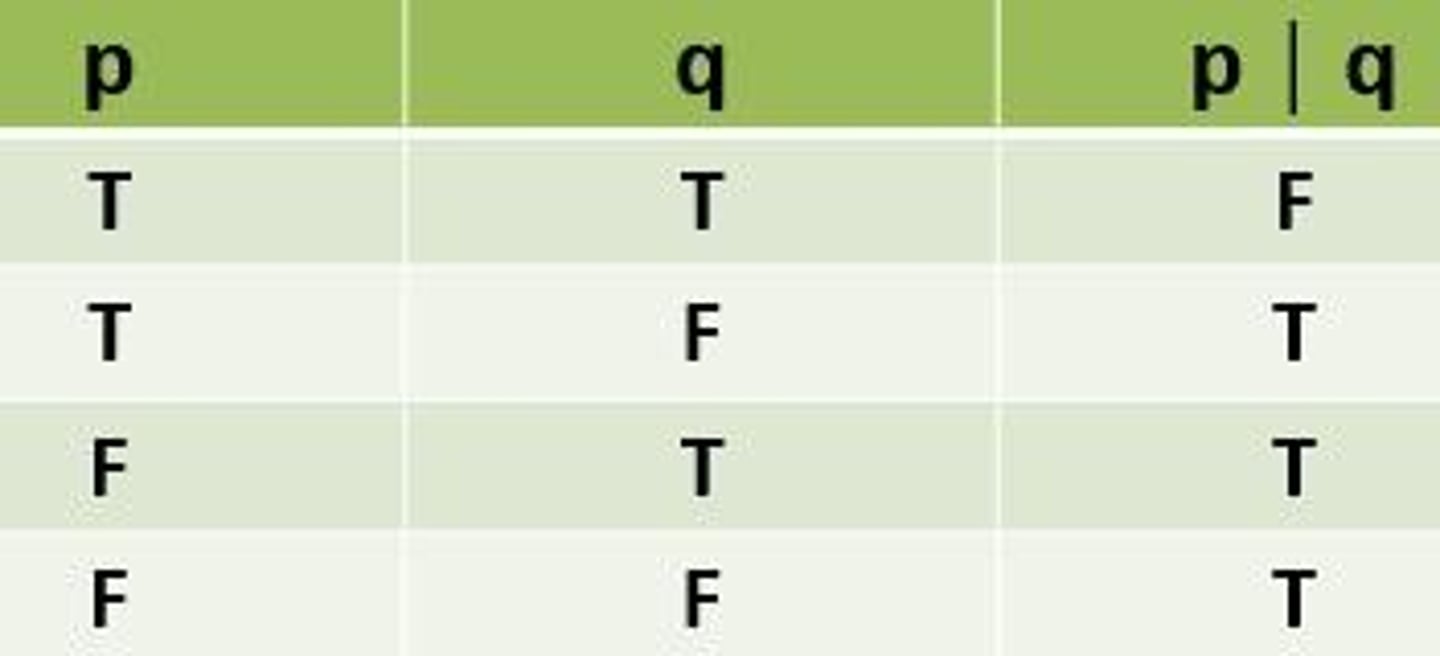
NAND

NAND operator produces a FALSE value only if both values of its two inputs (propositions) are TRUE.

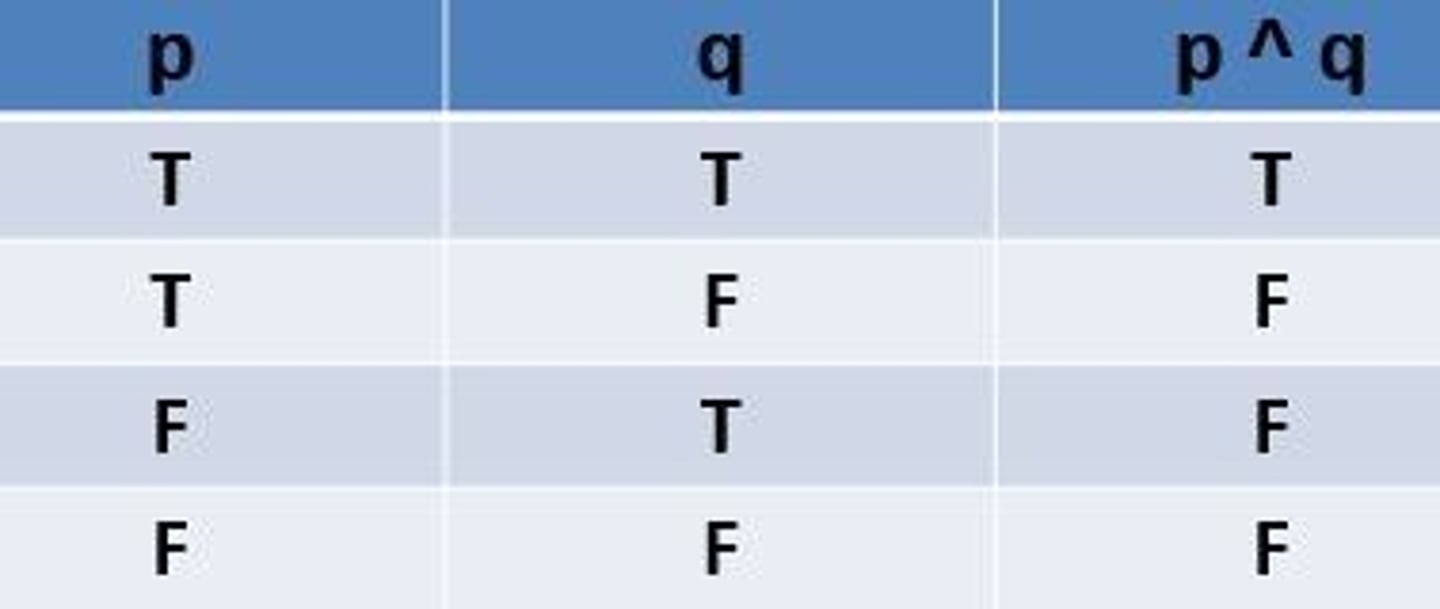
Conjunction

this proposition is TRUE if p and q are both TRUE

Disjunction

this proposition is FALSE only when both p and q are both FALSE.

Exclusive disjunction (XOR, EOR or EXOR)

a proposition that is TRUE when exactly one of p and q is TRUE and is FALSE otherwise.

Symbolic Logic

is the method of representing logical expressions through the use of symbols and variables, rather than in ordinary language.

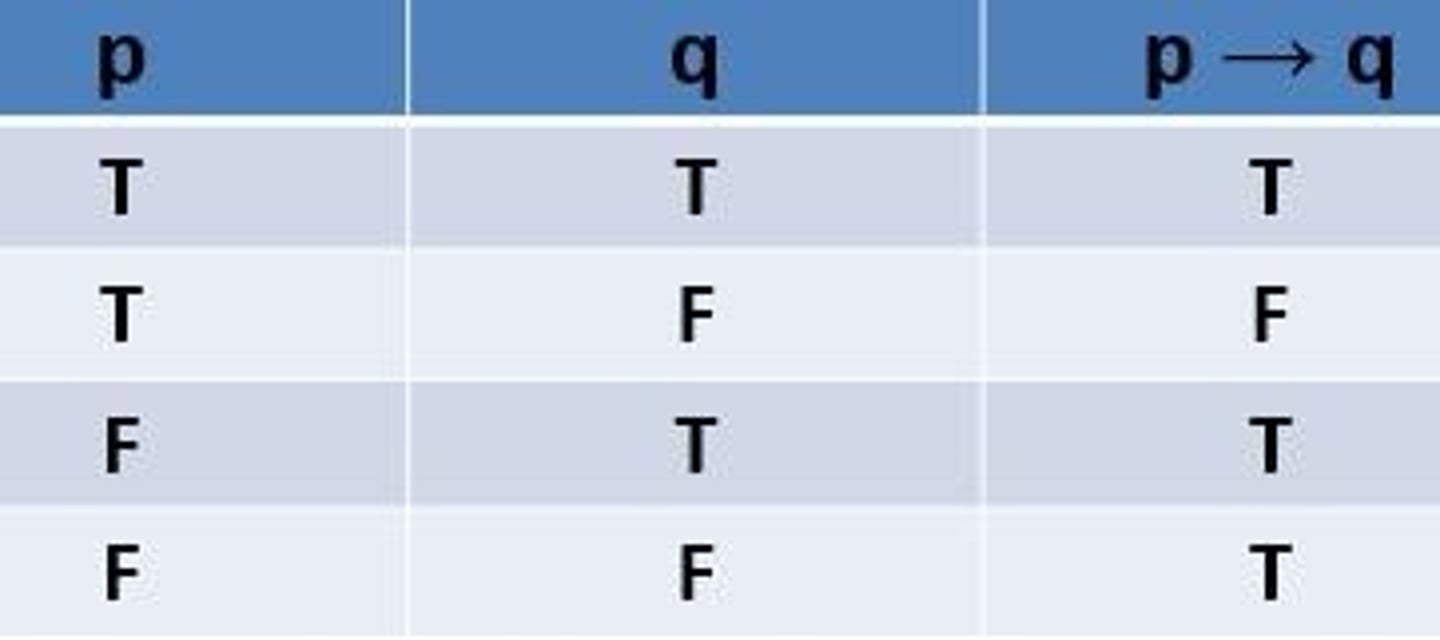
Implication

the statement p → q asserts that q is true on the conditional the p holds.

Inverse

~ p → ~ q

Contrapositive

~ q → ~ p

Declarative statement

declaring facts or mathematical statement.

Underlying principle of proof

Mathematical reasoning and arguments are based on the rules of logic.

Compound proposition example

Today is Monday and Julie is happy.

Conditional example

If it is raining heavily then classes are suspended.

Biconditional Statement

is simply the conjunction, compound statement, or a conditional statement with its converse.

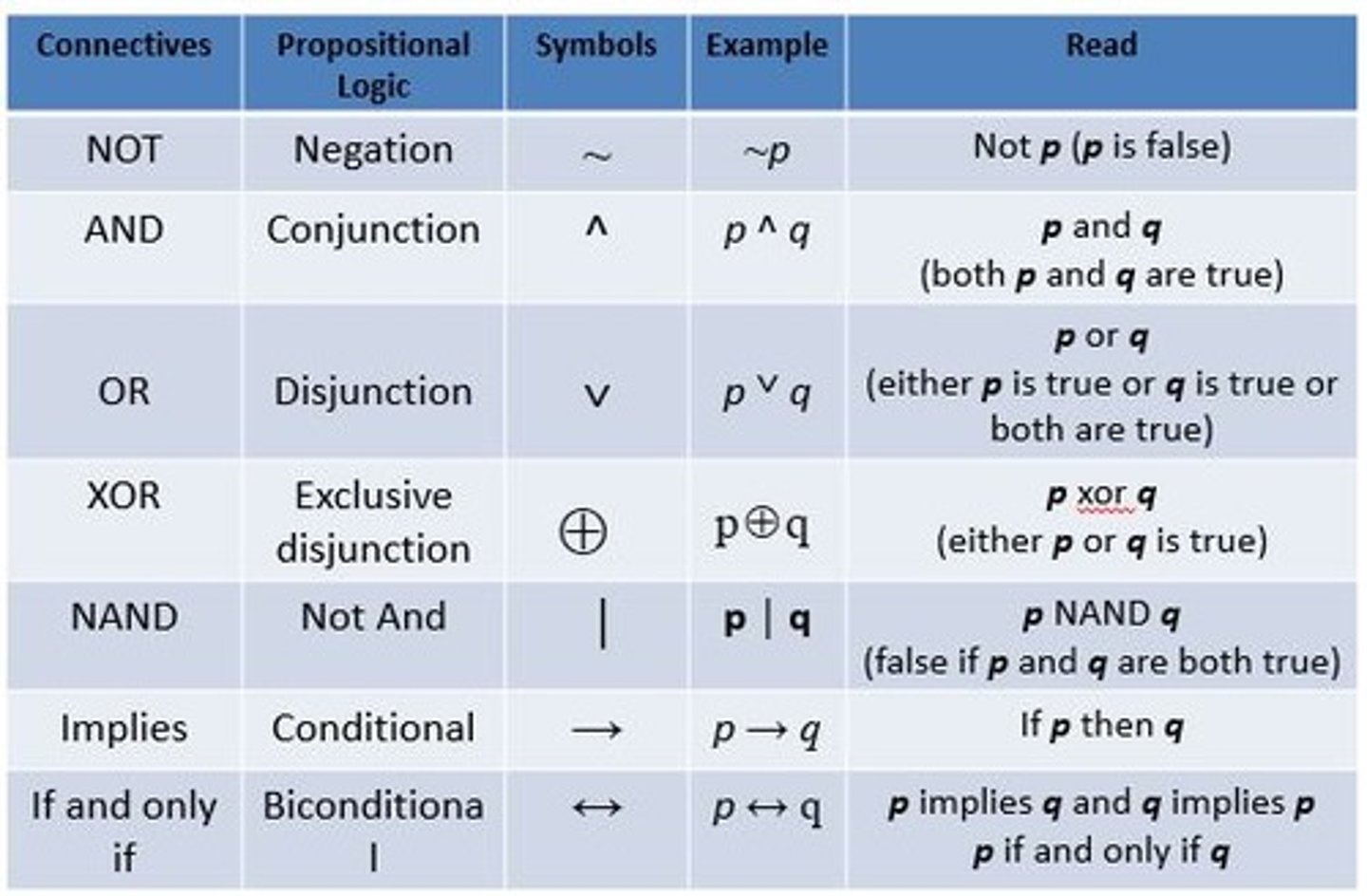
Truth Table

a diagram in rows and columns showing how the truth or falsity of a proposition varies with that of its components.

Assertion

Assumption that something is true.

Negation

an operation on one logical value, typically the value of a proposition, that produces a value.

Logical Equivalence

Two logical expressions are logically equivalent if they have the same truth values.

Biconditional

a relation between two propositions that is true only when both propositions are simultaneously true or false.

Tautology

a compound proposition if it is always true for all possible values of its propositional variables.

Contradiction

(also called absurdity) is a propositional form which is always false for all possible values of its propositional variables.

Contingency

A propositional form which is neither a tautology nor a contradiction.

Statement with k variables

has 2^k possible truth values assignments.

Truth values for variables

[1 variable - 2 truth values, 2 variables - 4 truth values, 3 variables - 8 truth values, 4 variables - 16 truth values, etc.]

p → q

is TRUE when both p and q are TRUE and when p is false, no matter what truth value q has.

Conditional

If it is raining heavily then classes are suspended.

~ p → ~ q

If it is not raining heavily then classes are not suspended.

~ q → ~ p

If classes are not suspended, then it is not raining heavily.

Propositions

p: If the price is right, then I will buy this item.