Interference (Part-V)

Reflection Phase Change (Fixed Boundary)

• ΔΦ = π (180°)

• The reflected wave is inverted

Reflection Phase Change (Free Boundary)

• ΔΦ = 0

• The reflected wave is not inverted

Incident–Reflected Amplitude (Ideal Boundaries)

• A_R = A_I

• For both fixed and free boundaries, the reflected wave has the same amplitude as the incident wave (ideal case).

Principle of Superposition

yR(x, t) = y1(x, t) + y2(x, t)

Linear Wave Equation

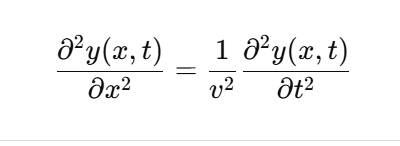
Traveling Wave Solution

• y(x, t) = f(x ± vt)

• Any function of x ± vt satisfies the linear wave equation.

Sinusoidal Wave Function

y(x, t) = Asin(kx - ωt + Φ)

Wave Number

k = (2π)/λ

Wave Speed (Sinusoidal Wave)

v = ω/k = fλ

Two Identical Waves with Phase Difference

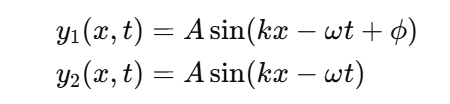
Trigonometric Identity for Superposition

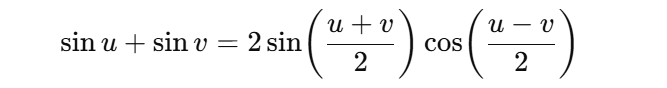
Resultant Wave from Two Identical Sinusoids

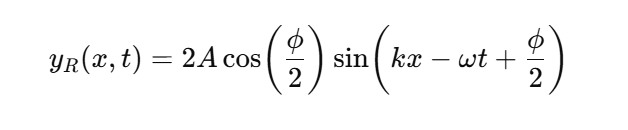
Resultant Amplitude (Phase Dependent)

A_R = 2Acos(Φ/2)

Constructive Interference Condition

If Φ = 0, then A_R = 2A

Destructive Interference Condition

If Φ = π, then A_R = 0

Partial Interference

If 0 < Φ < π
then 0 < A_R < 2A

Phase difference (Φ)

What Determines Interference Type?

λ, f, ω, and k

What Does NOT Change During Interference?

Linear Restoring Force → Linear Wave Equation → Valid Superposition

Why Small Amplitudes Matter?

Angular Frequency

ω = 2πf