AP Physics 2 Ultimate Guide
1/137
Earn XP
Description and Tags
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No analytics yet
Send a link to your students to track their progress
138 Terms
Density
________ is a positive scalar quantity.
Density
Mass per unit volume of a substance is defined as density.
Buoyancy
If a body is fully or partially immersed in a fluid, it experiences an upward force due to the fluid called buoyant force, and the phenomenon is called buoyancy.
The Volume Flow Rate
It is the volume of fluid that passes through a particular point per unit of time.
f = Av
f = volumetric flow rate
A = cross-sectional area
v = flow velocity v
Bernoulli’s Effect
At comparable heights, the pressure is lower where the flow speed is greater.
Air Flow
The air on the bottom has greater pressure and pushes up on the wing giving the airplane lift force
Pressure
Pressure is defined as the magnitude of the normal force acting per unit surface area.
P = F/A
P is pressure
F is force
A is the area
Pressure units
Pascal (Pa) 1 Pa = 1 N/m^2 Practical units: atm, bar, torr
Hydrostatic pressure
It is the pressure due to the liquid.
Continuity equation
The density of the fluid is constant.
A1V1 = A2V2 A1 and A2 (cross-sectional areas)
V1 and V2 (flow velocities)
Bernoulli’s Equation (Conservation of energy in liquids)
fluid is incompressible.
fluid’s viscosity is negligible.
fluid is streamlined.
the equation is very similar to the conservation of energy with total mechanical energy.
Heat
Thermal energy is transmitted from one body to another. Heat is energy in transit.
Temperature
It is a measure of an object’s internal energy.
Kinetic Theory of Gases
It relates to the macroscopic properties of gases such as pressure, temperature, etc.
Every gas consists of small particles known as molecules.
The gas molecules are identical but different from those of another gas.
The volume of molecules is negligible compared to the volume of gas.
The density of a gas is constant at all points.
Consequently, pressure is exerted by gas molecules on the walls of the container.
No attractive or repulsive force exists between the gas molecules.
The Ideal Gas Law
Pv = nRT
P = pressure
V = volume
n = no. of moles
R = Gas constant
T = temperature
Average Kinetic Energy
The pressure exerted by N molecules of gas in a container is related to the average kinetic energy.
K avg = 3/2 kb T
K avg = average kinetic energy
kb = Boltzmann’s constant
T = temperature
Root mean square velocity
It gives us a type of average speed that is easy to calculate from the temperature of the gas.
vrms = √3 kb T/ m
vrms = root mean square velocity
kb = Boltzmann’s constant
T = temperature
m = mass
The Maxell-Boltzmann Distribution
The Kinetic theory of gases applies to a large number of particles.
Some molecules will be moving faster than average and some much slower.
Heat Engines
It is a device which uses heat to produce useful work
Convection
The movement caused within a fluid by the tendency of hotter and therefore less dense material to rise, and colder, denser material to sink under the influence of gravity, which consequently results in transfer of heat
Radiation
Radiation is the emission or transmission of energy in the form of waves or particles through space or through a material medium.
Zeroth law of thermodynamics
If objects 1 and 2 are in thermal equilibrium with Object 3, then Objects 1 and 2 are in thermal equilibrium with each other.
First law of thermodynamics
It is a special case of the law of conservation of energy that describes processes in which only internal energy changes and the only energy transfers are by heat and work.
∆ U = Q + W
Q = heat added
W = work done by the system
∆ U = change in internal energy
work done
it is used to calculate work done.
Isothermal Process
Temperature remains constant.
Adiabatic process
no transfer of heat
Isobaric process
pressure remains constant
Isochoric process
volume remains constant.
Second law of thermodynamics
It describes how systems evolve over time.
Entropy
It is associated with a state of randomness, disorder, or uncertainty.
Conduction
Heat conducts from one point to another only if there is a temperature difference between the two objects.
Electric Charge
In an isolated system, the charge is always conserved.
Protons and electrons have a quality called electric charge.
The charge is invariant in nature.
The charge is quantized.
(Q = n e)e = 1.6 * 10^-19 C
n = no. of electrons
Q = charge
Ionisation
It involves addition or removal of electrons.
Coulomb’s Law
The electric force between two particles with charges q1 and q2 separated by distance r has a magnitude by the equation:
F = Kq1q2/r^2
F = force
K = coulomb’s constant
q1 and q2 = charges
r = distance between the charges
Electric Field
The space is surrounded by a charge in which another charged particle experiences the force.
Electric field due to a point charge
The electric field surrounding the point charge is:
E = 1/4πε0 * Q/r^2
E = electric field
Q = charger = distance between charges
ε0 = permittivity of free space
Three types of electric field
Radial field
It is generated by a collection of point charges.
An infinite sheet of charge.
electric field lines
The electric fields follow the same addition properties as the electric force.The electric field lines never cross.
The uniform electric field
A lot of problems deal with the uniform electric field.The field may be taken as uniform at least in the middle.The uniform field just signifies the constant force.
Conductors
Materials which allow the flow of excess charge without resisting it.
Insulators
Materials that resist the flow of electrons.
Charging by friction
It involves rubbing the insulator against another material, thereby stripping electrons from one to another material.
Charging through conduction
When we connect two conductors charge flows from one to another until the potential of both the conductors becomes the same.
Charging through induction
The process of charging by induction may be used to redistribute charges among a pair of neutrally charged spheres.
If the sphere is an insulator made up of glass
There aren’t any free electrons.The atoms make up the sphere will become polarised.
Electrical Potential Energy
We is the work done by the electric force, then the change in the charge’s electrical potential energy is defined by:
Ue = electrical potential energy
We = work done by electric force
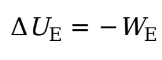
Electrical Potential Energy from a point charge
Electrical potential energy required to move along the field lines surrounding a point charge is given by:
q1 and q2 = charges
e0 = permeability of free space
Ue = electrical potential energy
r = distance
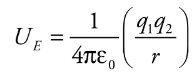
Electric Potential
Electric potential is the electric potential energy per unit of charge at a point in an electric field, measured in volts (V). It's the work done per unit charge in bringing a test charge from infinity to that point. V = U/q
Electric Potential Energy from a point charge
Consider the electric field created by a point source charge Q. If a charge moves from a distance rA to a distance rB from Q, then the change in the potential energy is: Ub and Ua = electrical potential energies for a and bra and rb = distances for a and be0 = permeability of free space
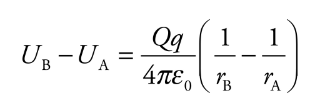
Equipotential Surface
An equipotential surface is a surface in a region of space where every point on the surface is at the same potential. In other words, no work is required to move a charge along an equipotential surface. Equipotential surfaces are perpendicular to electric field lines and can be used to visualize the electric field in a given region.
Addition of electric potential
V = kQ/r V = electric potential energyq = point charger = distance between any point around the charge to the point chargek = Coulomb constant; k = 9.0 × 109 N
Equipotential Curve
Equipotential curves are curves of constant elevation. If you walk along any of the contour lines and you neither ascend nor descend, then the curve is known as the equipotential curve.
Equipotential Map
A drawing of several equipotential curves at various values of the potential for a charge distribution is called an equipotential map.
Capacitor
Two conductors, separated by some distance carry equal but opposite charges +Q and -Q. The pair comprises a system called a capacitor.
Parallel-Plate Capacitor
The capacitor is in the form of parallel metal plates or sheets.
Capacitance
The capacitance measures the capacity for holding charge.
Fringing fields
Fringing fields extend beyond conductor or magnetic material edges. They weaken as the distance from the edge increases. They're important in device design but can cause interference and affect performance.
energy stored in capacitor
The energy stored in a capacitor can be calculated using the formula U = 1/2 * C * V^2 where U is the energy stored in joules, C is the capacitance of the capacitor in farads and V is the voltage across the capacitor in volts.
Dielectric
To keep the plates of the capacitor apart they are filled with dielectric which increases the capacitance of the capacitor.
Current
The continuous flow of charge
Average current
Iavg = change in charge/ change in time
Battery
A battery is a device that maintains an electric potential difference between the two terminals.
Direct current
The flow is from higher potential to lower potential. The electricity also flows in that direction called direct current.
Resistance
It is the impedance to the flow of electricity through a material. Asa charge moves through a material, it eventually hits a non-moving nucleus in the material.
Resistivity
It can be thought of as the density of nuclei the electrons may strike. R = ρ l / A R = resistance of the circuitρ = resistivityl = lengthA = cross-sectional area
low resistivity
conductors
high resistivity
insulators
resistors in series
R eq = R1 + R2
resistors in parallel
1/Req = 1/R1 + 1/R2
Ammeter
An ammeter is a device with a very low resistance that measures the current.
Voltmeter
It measures the electric potential called potential drop.
Ohm’s Law
V = IR R is the resistance in the circuit.V is the potential difference in the circuitI is the electric current
Power dissipation
P = VIP = I^2 RP = V^2 IRP is the powerV is the potential difference in the circuit.I is the electric current.
Kirchhoff’s rules
The loop rule states that the voltage drop across any complete loop in the circuit is 0V. This statement follows from the conservation of energy when applied to circuits.The junction rule states that the sum of all current flowing into any junction is equal to the current flowing out of the junction. This statement follows from the conservation of charge.
Capacitance
C = QV C = refers to the capacitance that we measure in faradsQ = refers to the equal charge that we measure in coulombsV = refers to the voltage that we measure in volts Besides, there is another formula that appears like this: C = kε0Ad C = refers to the capacitanceK = refers to the relative permittivityε0 = refers to the permittivity of free spaceA = refers to the surface area of the platesd = refers to the distance between places measured
Capacitors in parallel
Cp = C1 + C2
Capacitors in series
1/Cs = 1/C1 + 1/C2
Altering the capacitance of capacitor
Magnetic Field
The space surrounding a magnet is called a magnetic field.
Notation of magnetic field
We use (x) when the magnetic field goes into the plane.We use (.) when the magnetic field goes out of the plane.
Bar Magnet
A permanent bar magnet creates a magnetic field that closely resembles the magnetic field produced by a circular loop of current-carrying wire.
Magnetic Force
F = qv x B with magnitude: F = qv B sin theta F = forceq = chargev = velocityB = magnetic field
Right-Hand Rule
Whenever you use the right-hand rule, follow these steps: Orient your hand so that your thumb points in the direction of the velocity v. If the charge is negative, turn your thumb by 180 degrees.Point your fingers in the direction of B.The direction of FB will then be perpendicular to your palm.
Magnetic force on a current carrying wire
F = ILB with magnitude: F = BIL sin theta F = forceB = magnetic fieldI = currentL = length of conductor
Magnetic field created by current-carrying wire
B= μo I / 2πr B = magnetic fieldI = applied currentμo = permeability of free spacer = the distance from the wire where the magnetic field is calculated
Lenz’s Law
The induced current will always flow in the direction that opposes the change in magnetic flux that produced it. Emf = -N (ΔΦ/ Δt) ‘Emf’ = Induced voltage or electromotive force.‘N’ = The number of loops.‘Δϕ’ = Change within magnetic flux.‘Δt’ = Change in time
Faraday’s Law of electromagnetic induction
Whenever a conductor is placed in a varying magnetic field, an electromotive force is induced. If the conductor circuit is closed, a current is induced, which is called induced current.The induced emf in a coil is equal to the rate of change of flux linkage. emf = − dΦ/ dtemf = electromotive forcedΦ = change in magnetic fluxdt = change in time
Induced current
It is created in three ways: Changing the area of the loop of wire in a stationary magnetic field.Changing the magnetic field strength through a stationary circuit.Changing the angle between the magnetic field and the wire loop.
Motional Emf
Motional emf is the electromotive force generated by the motion of a conductor through a magnetic field.It is given by the equation emf = Blv, where B is the magnetic field strength, l is the length of the conductor, and v is the velocity of the conductor.This phenomenon is used in various applications, such as electric generators and motors.
Solenoid
Solenoid is a device that is constructed by a series of coaxial wires through which a continuous current flow.
Electromagnetic waves
Electromagnetic waves are a type of wave that consists of oscillating electric and magnetic fields that travel through space at the speed of light. They are produced by the acceleration of charged particles and include radio waves, microwaves, infrared radiation, visible light, ultraviolet radiation, X-rays, and gamma rays. Electromagnetic waves have a wide range of applications, including communication, medical imaging, and energy production.
Electromagnetic Spectrum
It can be categorized by its frequency. The full range of waves is called the electromagnetic spectrum.
Interference
The phenomenon of superimposition of two or more waves having the same frequency emitted by two coherent sources.
Diffraction
It is defined as the interference or bending of waves around the corners of an obstacle or through an aperture into the region of the geometrical shadow of the obstacle/aperture.
Single-Slit Experiment
A diffraction pattern will also form on the screen if the barrier contains only one slit.
Young’s Double Slit Experiment
The incident light on a barrier that contains two narrow slits, separated by distance d. On the right there is a screen whose distance from barrier L, is much greater than d.
Constructive and Destructive Interference
constructive interference: d sinθ = m λ destructive interference: d sinθ = (m+1/2) λ where, m = 0, 1, 2, 3, etc.λ = wavelength of lightd = distance
Angle of incidence
The angle that the incident beam makes with the normal is called the angle of incidence.
Angle of reflection
The angle that the reflection makes with the normal is called the angle of reflection.
Angle of refraction
The angle that the transmitted beam makes with the normal is called the angle of refraction.