Inferential statistics

Significance:

• means probably true (not due to chance) 

Power:

• increase chances of rejecting a false null hypothesis 

What is probability:

• Likelihood of something occurring 

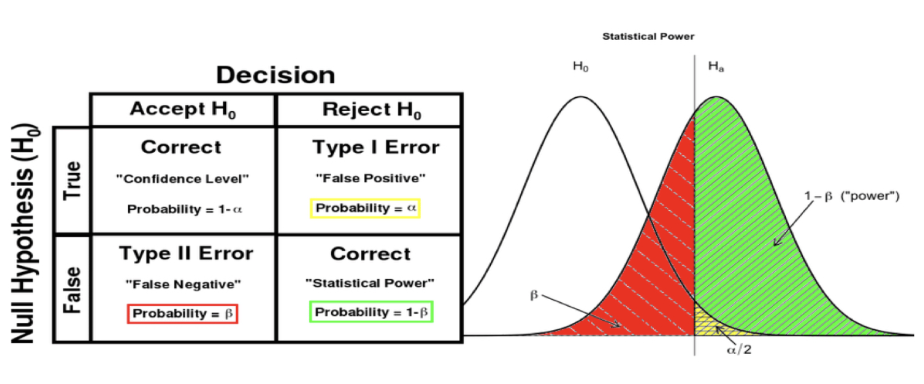
Type I error:

• we reject the null hypothesis in our sample, even though the null hypothesis is true for the population 

• By reducing risk of type I error, we increase chance of type II error 

Type II error:

• we retain the null hypothesis in our sample, even through the null hypothesis is false for the population (worse) 

• Decrease type II error by: increasing treatment effects, decreasing measurement error, using a more sensitive design 

P<.05:

• we are making a type I error less than 5 times out of 100 

What is done to control error:

• Reduce type I error by reducing significance level 

• Trade off is increasing risk of type II error and losing power 

General Linear Model : basis for most statistical analyses in social research:

• A system of equations that is used as the mathematical framework for most the statistical analyses used in applied social research 

T-test:

• good statistical procedure to see if means of two groups are significantly different 

**How to test for significance: 

1. Statement of the null hypothesis: assumption is there is nothing going on

2. Establishing the level of risk associated with the null hypothesis 

3. Selection of the appropriate statistical test 

4. Computation of the test statistic value

5. Determination of the value needed for rejection of the null hypothesis using the appropriate table of critical values for the particular statistic 

6. Comparison of the obtained value to the critical value

7. If the obtained value is more extreme than the critical value, the null hypothesis cannot be accepted 

8. If the obtained value does not exceed the critical value, the null hypothesis is the most attractive explanation 

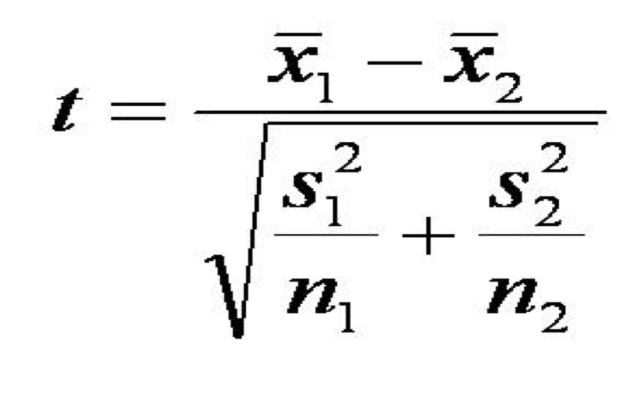
Explain how to increase the power of a t-test:

• Power: increasing probability of rejecting null hypothesis when null hypothesis is actually false 

**Increasing power in a t-test: 

1. Show a greater difference in the means of the two groups by using a better and stronger treatment

2. Reduce variance in groups by applying treatments and using control variables to reduce difference between participants 

3. Increase number of subjects in study 

• When T is found to be significant, we are saying that the true variance exceeds the error variance

Check to see if a correlation is significant:

• Choose desired significance level .05 or .01

• Determine degrees of freedom (number of subjects corrected for sample bias) N-2

**10 subjects at significance of .05 level and you find a correlation of .54

• Now check Critical value table: Df(8)= .6319

**Since correlation is less than critical value, your correlation is not significant

Factors in using correlations to infer (sample size, p level, coefficient of determination):

• Sample size – Larger samples provide more stable and reliable correlation estimates.

• p-level (statistical significance) – Indicates whether the correlation is likely due to chance.

• Coefficient of determination (r²) – Shows how much variance in one variable is explained by the other.

ANOVA:

• analysis of variance (the ANOVA helps keep the significance level) 

• A large treatment effect + within group variability = > 1.0

F values and rejecting the null:

• If the null hypothesis is true, we expect an F value of 1.0 

• If the null hypothesis is rejected, it is because the F value is significantly larger than 1.0

Do a Chi-square calculation and determine significance of the research:

Restrictions in using the Chi-Square test:

Requirement / Restriction	Explanation
Data must be frequencies	Cannot use means or percentages
Independent observations	No one counted twice; no paired samples
Minimum expected cell size	≥ 1 for all cells; ≥ 5 for most cells
Sufficiently large sample	Needed to approximate Chi-Square distribution
Mutually exclusive categories	Each observation belongs to only one category
Cannot infer strength or direction	Only tests association or difference

Concept of significance versus meaningfulness:

1. Statistical significance in and of itself is not very meaningful unless the study has a sound conceptual base that lends some meaning to the significance of the outcome

2. Statistical significance cannot be interpreted independently of the context within which it occurs 

3. While statistical significance is important as a concept, it is not the end-all. This is why we test hypotheses, not try to prove them

Explain concept of why we use .05 significance level:

• A Type I error = rejecting the null hypothesis when it is actually true.

Setting α = .05 means:

• We accept a 5% chance of falsely concluding that there is an effect or difference when there really isn’t.

• In the long run, if we repeated the study many times, only 5% of tests would incorrectly show significance when H₀ is true.

So α = .05 is a balance between being too strict and too lenient.

Explain concept of degrees of freedom:

• Total participants in investigation minus number of groups in study

• N-2

Explain what we can and cannot conclude from a significance test:

A significance test CAN tell us…	A significance test CANNOT tell us…
Whether to reject H₀	Whether H₀ is true
Whether the result is unlikely by chance	If the effect is large or meaningful
If evidence supports an effect/relationship	If the result proves causation
Direction of the effect (one-tailed)	The probability H₁ is true
	Conclusions beyond the sampled population