Math ISCI 1A24 - Midyear Exam Definitions

What is a Function?

• A function f:x → y is a method for assigning values in Y to values in X. Typically, X and Y will be sets of real numbers.

  • Terminology: X is called the domain of f

  • Terminology Y is called the codomain of f

Definition of Range

range f(x)={y\in\mathbb{R}:\forall x\in\mathbb{R}}

Definition of Injectivity

Suppose that I is a set of real numbers and f:I → R, then we can say that f is injective/one-to-one iff.
\forall x_1,x_2,\in I(x_1\neq x_2\rightarrow f(x_1)\neq f(x_2)) injectivity implies that there is a unique inverse.

A Function is Decreasing If

\forall x_1,x_2,\in I\left(x_1<x_2\to f\left(x_1\right)>f\left(x_2\right)\right)

A function is increasing if

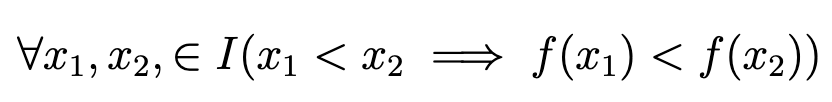
Definition of an Inverse

Suppose f: I → R is a function on an interval I. Then we can say that “f is invertible (on I)” if there is a unique function, g, such that:

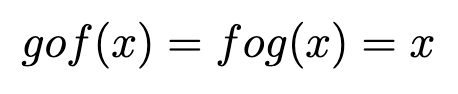
Definition of Log Function

For b>0, b≠1, we define log_b(x) to be the unique inverse of b^x

Word Definition of Epsilon-Delta Definition of a Limit

If you choose any small neighborhood around L (i.e. (L-ε, L+ε)) one can find a small enough neighborhood around c (i.e. (c-δ, c+δ)) such that if we we pick any x ∈ (c-δ, c+δ), x≠c, we get f(x) ∈ (L-ε, L+ε).

Epsilon-Delta Definition of a Limit

Assume f(x) is defined at least in a neighbourhood around a point c. We will say: lim_x→c f(x) = L iff

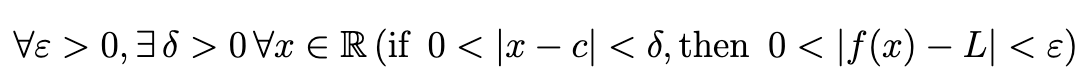
One-sided Definition of Limit (from Right)

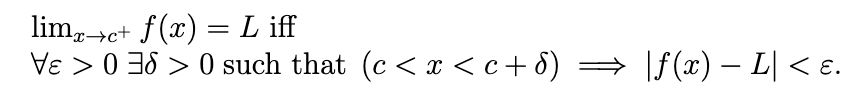
One-sided Definition of Limit (from Left)

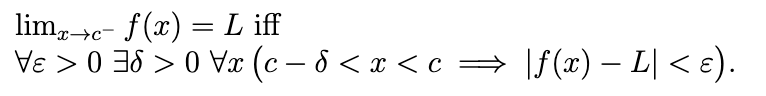
Definition of Continuity

Let f: I → ℝ, where I is some subset of ℝ. Assume that f is defined at least on some neighbourhood of a point c. Then we say that f(x) is continuous at the point x=c iff f(c) is defined and lim_x→c f(x) = f(c)

Intermediate Value Theorem

Suppose f(x) is continuous on a closed interval [a,b]:
for any d ∈ ℝ if either

1. f(a) ≤ d ≤ f(b) OR

2. f(a)≥ d ≥ f(b)

then there exists some c∈[a,b] such that f(c)=d.

Definition of a Derivative

Suppose f(x) is defined at least on a neighborhood around a point x=c. Then we can say that the derivative of f(x) at the point c (if it exists) is the limit:

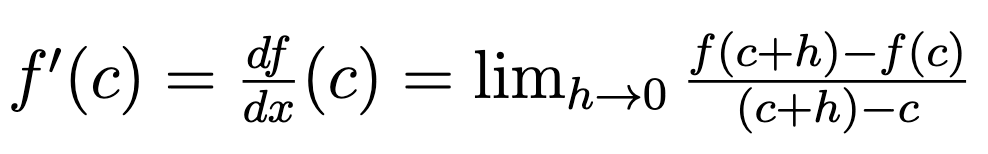
Definition of Parametric Curve

A parametric curve on ℝⁿ is described by functions x₁(t), … , x_n(t) of some parameter t. It is given by C: ℝ → ℝⁿ

C(t) = (x(t), y(t))

• Translates to a position in the x-y plane (in the case of ℝ → ℝ²) at time t.

Definitions of Absolute Extrema

Definition of Local Extrema

At least on some small neighbourhood surrounding c, f has a maximum or minimum restricted to that neighborhood

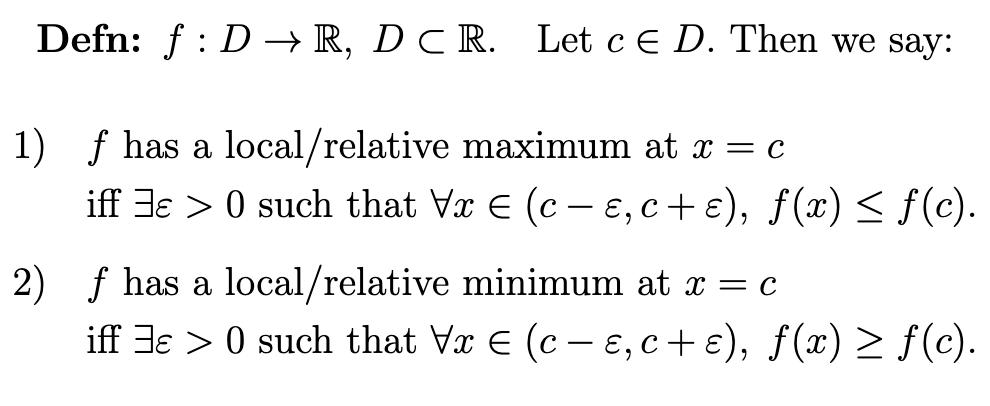
Fermat’s Theorem (local max and min)

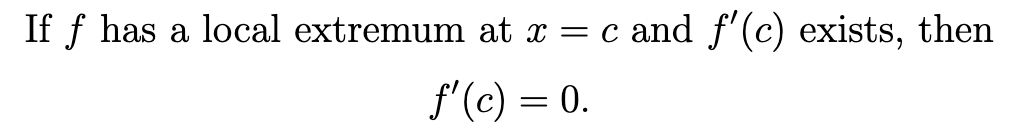
Extreme Value Theorem

Textbook defn: If f is continuous on a closed interval [a,b], then f attains an absolute maximum value f(c) and an absolute minimum value f(d) at some numbers c and d in [a,b].

Greg defn: If f: [a,b] → \mathbb{R} is continuous then an absolute max and an absolute min exist for f on [a,b] and they must occur at a critical value (either f’(c)=0, f’(c) DNE, or c=a or c=b)

Criteria for a critical point

Mean Value Theorem

Suppose f(x) is differentiable on [a,b] then \exists c \in [a,b] with f’(c)=\frac{f(b)-f(a)}{b-a}.

Definition of Inflexion Point

For a function f(x), we say that c is an inflection point if f(x) changes concavity at x=c. If f’(x) is differentiable and f(x). has an inflection point at x=c, then f’’(c)=0.

Concave Upwards

If the graph of F lies above all of its tangents on an interval I, then F is concave upward on I.

Concave Down

If the graph of f lies below all of its tangents on I then f is called concave downward on I.

Concavity Test

• if f’’(x)>0 on an interval I, then the graph of f is concave upward.

• if f’’(x)<0 on an interval I, then the graph of f is concave downward.

Second Derivative Test

Suppose f’’ is continuous near c.

• If f’(c)=0 and f’’(c)>0, then f has a local minimum at c.

• If f’(c)=0 and f’’(c)<0, then f has a local maximum at c.

Definition of a Differential Equation

A differential equation (in one variable x) is an equation of the form F(y⁽ⁿ⁾, y^(n-1), …, y, x) = 0.

• Note the highest derivative that appears is called the “order”. For instance, the derivative of x² is first order with respect to x.

Definition of an Initial Value Problem (IVP)

L’hôpital’s Rule

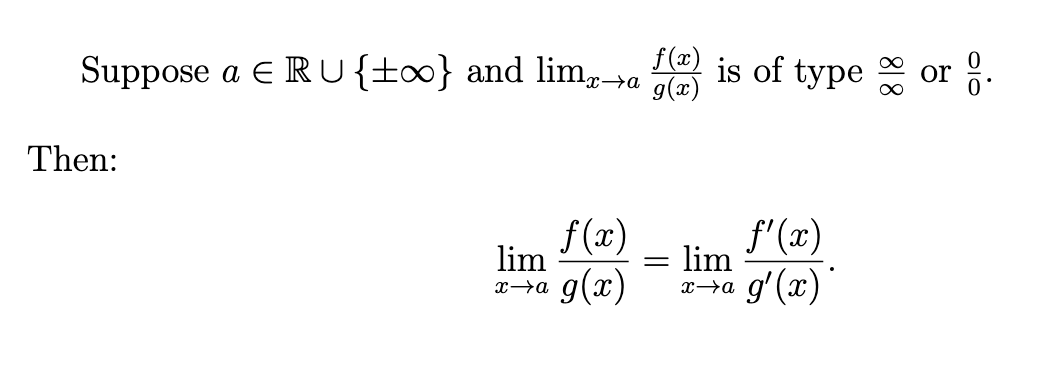
Euler’s Method

Approximates values for the solution of the initial-value problem y’ = F(x,y), y(x₀) = y₀, with step size h, at x_n = x_n-1 + h, are
y_n=y_n-1 + hF(x_n-1, y_n-1) n= 1, 2, 3,…

Definition of an Antiderivative

Suppose we have a function f(x) we say that F(x) is an antiderivative (an because there may be multiple suitable antiderivatives) of f(x) if y=F(x) is a solution to the differential equation:

y’=F(x)\Leftrightarrow\frac{d}{dx}F\left(x\right)=f\left(x\right)

In other words, F(x) is an anti-derivative of f(x) if (see image) the derivative of F(x) is f(x) .

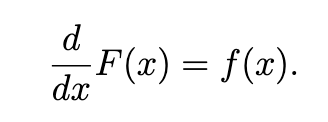
Fundamental Theorem of Calculus (part 2)

Suppose f(x) is such that an antiderivative F(x) exists on [a,b].

Let x_1=a,\Delta x=\frac{b-a}{n},x_{i}=a+i\Delta x for 1\leq i \leq n

Then

A=\lim_{n\to\infty}\sum_{i=1}^{n}f(x_{i})\,\Delta x=F(b)-F(a)=\int_{a}^{b}\!f\left(x\right)\,dx

In other words: we can find the area under f(x) on an interval [a,b] by computing F(b)-F(a) for any antiderivative F(x).

Other definition Greg gave that is easier to remember:

If F’(x) = f(x)" on [a,b], then we can evaluate \int_{a}^{b}\!f\left(x\right)\,dx as

\int_{a}^{b}\!f\left(x\right)\,dx=F\left(b\right)-F\left(a\right)

Fundamental Theorem of Calculus (part 1)

If f(x) is integrable on [a,b] then the function
F(x)=\int_{a}^{b}\!f\left(x\right)\,dx is an antiderivative of f(x).

Rolle’s Theorem

Let f be a function that satisfies the following three hypotheses.

1. f is continuous on the closed interval [a,b].

2. f is differentiable on the open interval (a,b).

3. f(a)=f(b)

Then there is a number c in (a,b) such that f’(c)=0.

State the First Derivative Test

if f(x) is differentiable at c and f’(c)=0, then if

1. f’(x)>0 on some interval (c-\epsilon,c) and f’(x)<0 on some interval (c, c+\epsilon) then f(c) is a local max.

2. f’(x)<0 some interval (c-\epsilon,c) and f’(x)>0 some interval (c, c+\epsilon) then f(c) is a local min.

State the Second Derivative Test

if f’’(c) exists and f’(c)=0 then:

1. if f’’(c)<0 then f(c) is a local min.

2. if f’’(c)>0 then f(c) is a local max.

3. if f’’(c)=0 the test is inconclusive.

State L’hôpitals Rule

For a limit of the form \lim_{x\to c}\frac{f(x)}{g(x)} if \lim_{x\to c}f(x)=0=\lim_{x\to c}g(x) or \lim_{x\to c}|f(x)|=\infty=\lim_{x\to c}|g(x)| , then \lim_{x\to c}\frac{f(x)}{g(x)}=\lim_{x\to c}\frac{f^{\prime}\left(x\right)}{g^{\prime}\left(x\right)} .