Time Series Analysis and Forecasting: Components, Models, and Smoothing Techniques

What is a time series?

A sequence of data points collected or recorded at regular time intervals.

Give a business example of a monthly time series.

Car sales numbers each month.

Give a business example of a quarterly time series.

Smartphone sales worldwide each quarter.

Give a business example of a weekly time series.

Orders on Amazon every week.

Give an economic example of a monthly time series.

Inflation rate every month.

Give an economic example of a quarterly time series.

Country's GDP growth rate every quarter.

Give an economic example of an annual time series.

Unemployment rate every year.

What are the main components of a time series?

Trend, Seasonality, Cycle, Residual/Noise.

What is a trend in a time series?

Long-term upward or downward movement.

What is seasonality in a time series?

Repeating patterns over fixed periods.

What is a cycle in a time series?

Patterns that repeat but not on a strict schedule.

What does residual/noise refer to in a time series?

Random fluctuations.

How do trend, seasonality, and noise differ?

Trend shows long-term progression, seasonality captures repeated short-term cycles, and residual reflects random noise.

Why is stationarity important in time-series modeling?

Most time series models assume stationarity.

How do you visually detect non-stationarity in a time plot?

Look for trends, changing variance, or seasonality.

Define mean in statistics.

Mean is the sum of values divided by the number of values.

What is variance?

Variance measures how spread out data is.

What is standard deviation?

Standard deviation is the square root of variance.

What does correlation measure?

The relationship between two variables.

Give an example of positive correlation.

Ice cream sales increase as temperatures rise.

What is the rule for the union of two events?

The union of events A and B is when either A or B or both occur.

How do you compute the complement of an event?

The complement consists of all outcomes that do not result in event A.

When are two events mutually exclusive?

When they cannot happen at the same time.

Why do we apply smoothing to time series?

To reduce random variation, highlight trends, and make forecasting easier.

What is a simple moving average (SMA)?

Average of past n periods.

What happens when the length of the moving-average window increases?

The data series becomes smoother but introduces greater lag.

What is exponential smoothing?

A method that gives exponentially higher weight to recent data.

How does exponential smoothing differ from SMA?

SMA gives equal weight to all data points, while exponential smoothing gives more weight to recent data.

What is the role of α (alpha) in Simple Exponential Smoothing?

It controls the weight given to recent observations.

When should median smoothing be used?

When data has outliers.

Why is Lowess smoothing useful?

It fits a smooth curve to local subsets of data.

What is an m-moving average?

A type of moving average calculated as the average of the last 'm' data points.

Why can't moving averages be computed at the endpoints?

They require data points outside the bounds of the dataset.

How does a centered moving average work?

It averages values from a window of data points around the central point.

Why is a 2×12 moving average used for monthly data?

To eliminate the seasonal component and produce a centered estimate of the trend.

What are the components of the ETS framework?

Error, Trend, Seasonal.

What model corresponds to simple exponential smoothing (SES)?

ETS(A,N,N).

How do we interpret a large α (close to 1)?

More weight is given to recent observations.

What does Holt's linear trend method capture that SES cannot?

A linear trend component.

Why do we use a damping parameter in the damped trend model?

To gradually reduce the strength of the trend in future forecasts.

What is the difference between additive and multiplicative seasonality in Holt-Winters?

Additive seasonality adds seasonal effects, while multiplicative seasonality multiplies them.

What is additive seasonality in Holt-Winters?

Additive seasonality adds fixed seasonal amounts to the trend.

What is multiplicative seasonality in Holt-Winters?

Multiplicative seasonality multiplies the trend by seasonal factors.

How do you check whether a series is stationary?

A stationary series is roughly horizontal, has constant variance, and shows no long-term predictable patterns.

How does the ACF of a non-stationary series typically look?

The ACF of non-stationary data decreases slowly.

What does first differencing remove?

First differencing removes linear trends and unit-specific effects from time series.

What does seasonal differencing remove?

Seasonal differencing removes recurring, predictable patterns from a time series.

What is over-differencing, and why is it harmful?

Over-differencing applies differencing more times than necessary, causing loss of valuable information and increased variance.

What is the purpose of the KPSS test?

The KPSS test determines if a time series is stationary or has a unit root.

How does the ndiffs() function help in ARIMA modeling?

It automatically determines the optimal number of differences needed to make a time series stationary.

What is an AR(p) model?

An AR(p) model predicts future values based on a linear combination of its own past values.

What is an MA(q) model?

An MA(q) model is a time series model where the current value is a linear combination of past random shocks.

What does the 'd' in ARIMA(p,d,q) represent?

The degree of differencing.

How do you interpret a seasonal ARIMA model notation like (P,D,Q)m?

It captures non-seasonal patterns with (p,d,q) and seasonal dynamics with (P,D,Q) over a m-period cycle.

When is seasonal differencing required?

When a time series exhibits a strong, repeating seasonal pattern.

What criteria are used to select between ARIMA models?

Criteria include AIC, AICc, BIC for model selection, and RMSE, MAPE for performance evaluation.

Why does a lower AICc indicate a better model fit?

It balances good fit with model simplicity, penalizing complexity to prevent overfitting.

Why might a model with lower RMSE be preferred for forecasting?

It indicates higher accuracy and more reliable predictions.

What is time-series decomposition?

A method to break down a time-dependent dataset into Trend, Seasonality, and Residuals.

What is the additive decomposition equation?

Not provided.

What is the multiplicative decomposition equation?

Not provided.

When should additive vs multiplicative decomposition be used?

Additive is used for constant seasonal swings; multiplicative for varying seasonal effects.

What is STL decomposition and why is it preferred over classical decomposition?

STL decomposition is robust to outliers and allows for seasonal changes.

What is a TSLM model used for?

Time Series Linear Model used for forecasting with trend and seasonality.

How do time trend and seasonal dummies help in forecasting?

They capture trends and seasonal effects in the data.

How do you interpret a regression coefficient in a time-series context?

It indicates the change in the dependent variable for a one-unit change in the predictor.

How do you check whether regression residuals look like white noise?

By analyzing the ACF and checking for randomness.

What is a point forecast?

A single value prediction for a future observation.

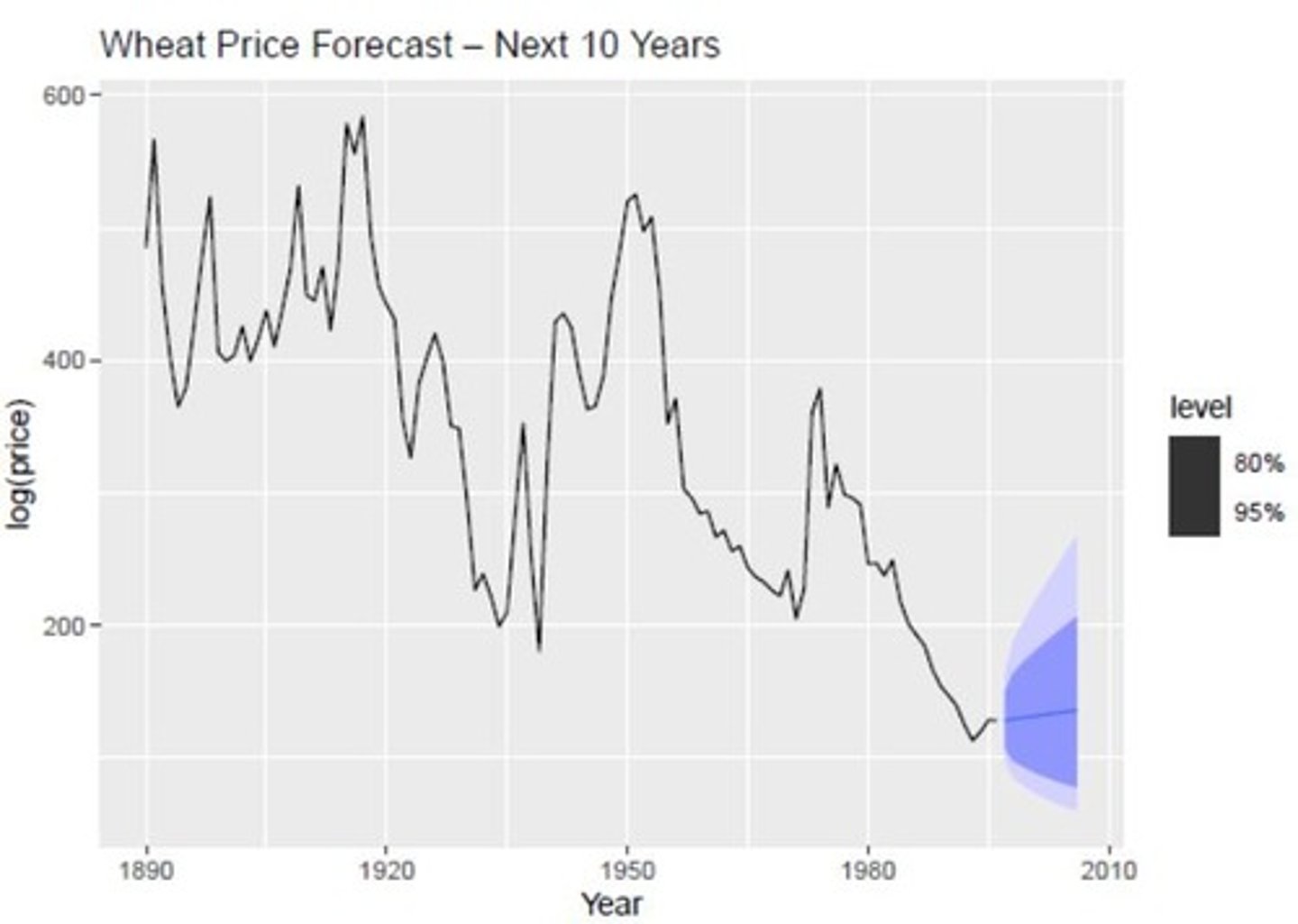
What happens to prediction intervals as the forecast horizon increases?

Forecast intervals widen over time.

What are 'random futures' and why are they useful?

They represent possible future outcomes, useful for risk assessment.

Why do forecast intervals widen over time?

Uncertainty increases with the forecast horizon.

What model type is needed when the seasonal pattern grows with the level?

A multiplicative model.

Which model should you choose if RMSE of ETS is lower but AICc of ARIMA is lower?

Choose based on the context; lower RMSE indicates better accuracy, while lower AICc suggests better model fit.

Why might a model have good in-sample fit but poor forecasting performance?

It may be overfitting the training data.

What does slow decay in ACF imply?

It suggests non-stationarity in the time series.

What does a strong spike at lag 4 in ACF suggest?

It indicates a significant relationship with a lag of 4 periods.

What does α = 0.90 in SES tell you about the model?

It indicates a strong emphasis on recent observations.

What does β* = 0.30 in Holt's model mean?

It indicates a moderate level of smoothing for the trend.