Circular Motion; Work & Energy; Linear Momentum

Centripetal (Radial) Acceleration

an object moving in a circle of radius r at constant speed v has an acceleration whose direction is toward the center of the circle

acceleration is dependent on v and r- the greater the speed, the faster the velocity changes direction; the larger the radius, the less rapidly velocity changes directio

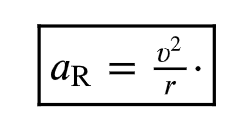
Period

the time required for an object revolving in a circle to make one complete revolution; represented by a T

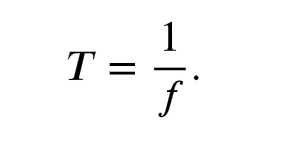
Velocity of Object Revolving in Circle

velocity is the change in position over some time interval T; use circumference of circle to find distance (2πr)

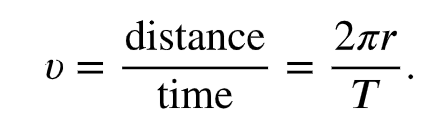
Forces on Object in Circular Motion

use Newton’s second law for the radial component

since the acceleration is directed toward the center of the circle at all times; the net force must also be directed toward the center 

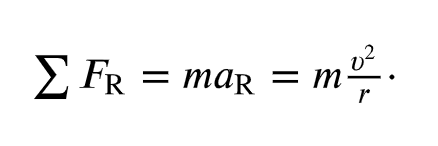
Centripetal Force

describes the direction of the net force needed to provide a circular path; always directed toward the center of the circle and applied by other objects

NOT a new kind of force or a force that exists in nature on its own

ex: tension (like a ball on a string), static friction (like a car going into a turn); gravity (like the earth’s attraction to the sun)

Free-Body Diagram for Circular Motion

force points toward inside of circle; weight (mg) always points downward regardless of position of object

Speed Where No Friction Is Required

FN sin theta = m v²/r

Magnitude of Gravitational Force

F_G = G (m₁m₂ / r²)

m_1 and m_2 are the masses of two particles, r is the distance between them, and G is a universal constant which must be measured experimentally

Force of Gravity Near Earth’s Surface

F_G = G (mm_e / r_e²)

G Constant

6.667 × 10^-11 N . m²/kg²

Acceleration of Gravity at Earth’s Surface

g_e = G (m_e/r_e²) = 10.0 m/s²

Acceleration of Gravity at Planet’s Surface

g_p = G (m_p/r_p²)

Earth’s Mass and Radius

5.98 × 10²⁴ kg

6378 km (use 6400 km?)

Potential & Kinetic Energy Formulas

PE = (mg)y

KE = ½ mv²

Work

product of the magnitude of the displacement and the force

force and displacement must be going in the same direction to be valid

W = F times x

Friction Work

W= Ffr x dfr

W= (mu FN) dfr

Spring Work Formula

Wspring = ½ kx²

where k is spring constant in N/m and x is compression in m

Power

power is equal to energy or work over time = J / s = watt

1 horse-power = 750 watts

P = work/t = F x x/t = FxV

Linear Momentum

product of its mass and its velocity

the more momentum an object has, the harder it is to stop it

P = mv

Newton’s 2nd Law Rewritten for Momentum

the rate of change of momentum of an object is equal to the net force applied to it

ΣF = Δp / Δt = mv_f-m₀ / Δt

Conservation of Momentum

the total momentum of an isolated system of objects remains constant; i.e., momentum before = momentum after

m_A1v_A1 + m_B1v_{B1 =} m_A2v_{A2 +} m_B2v_B2 

ΣF_net = 0 (if equal to 0, then Δp must be equal to 0)

Impulse Momentum

impulse = F_net x Δt

Elastic Collision

K_E is conserved, P (momentum) is conserved

in one dimension:

Inelastic Collision

when no outside forces are acting on system

P (momentum) is conserved if K_E is not conserved

Collisions in Two Dimensions

Momentum Conservation & Collisions Steps

1.) choose system

2.) consider whether significant net forces act on chosen system

3.) draw a diagram

4.) choose coordinate system and assign positive and negative

5.) apply momentum conservations equations

6.) if elastic, you can alos write down a conservations of kinetic energy equation

7.) solve for unknowns

8.) check work, check units, ask if results make sense/are reasonable