Lecture 3 - Discrete-Time Solow Growth Model

What is the basic setup of the discrete-time Solow model, and what question is it designed to answer?

model how capital accumulation (ΔK) affects output and whether this growth is sustainable

4 → 3 equations

4 → 1 equations

Solow Model Alternative notation

CRS & DRS

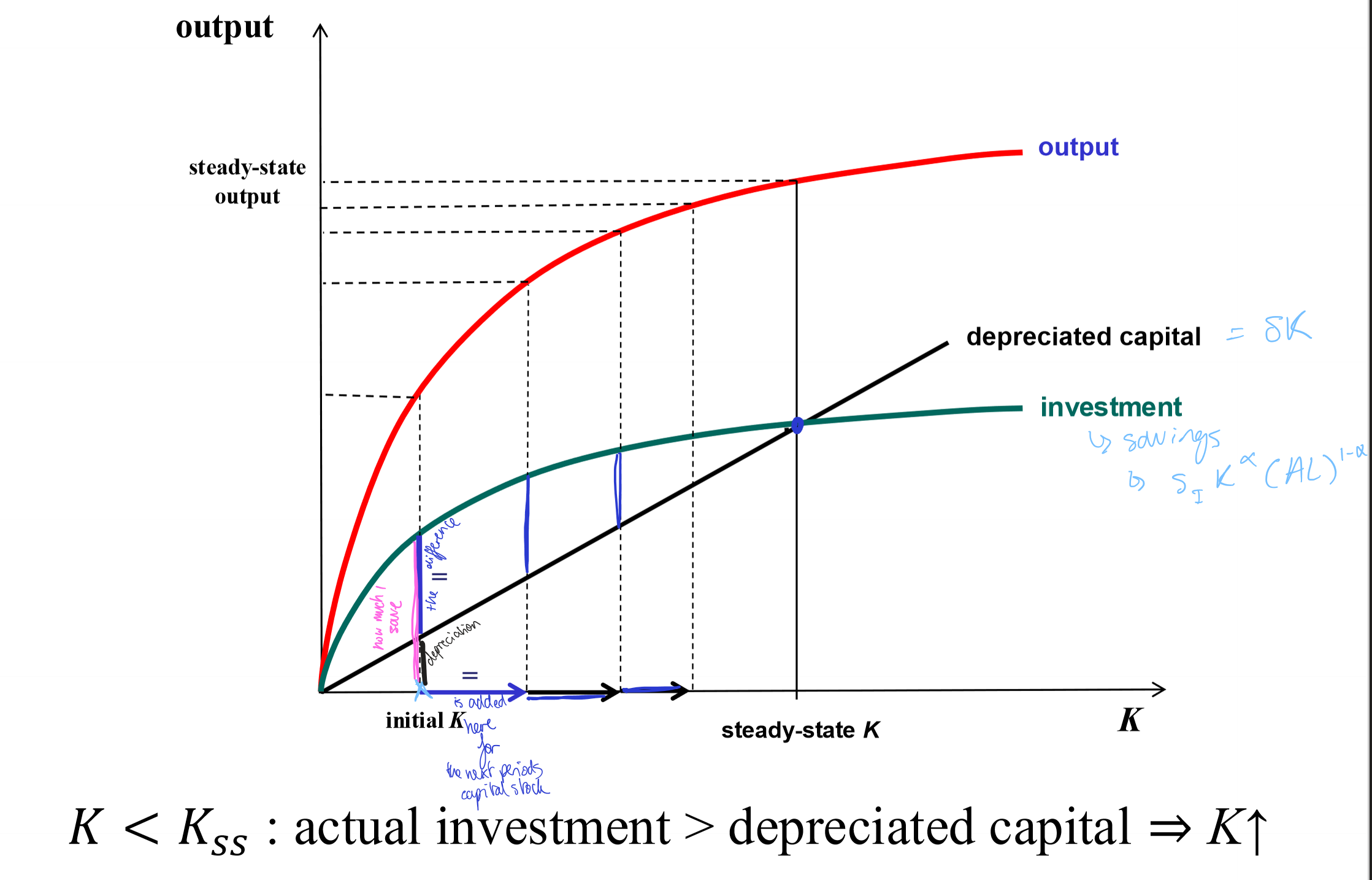
How does capital evolve in the Solow model, and what defines the steady state?

Change in the capital stock = next period’s capital minus today’s capital (investment minus depreciation)

Starting below steady state

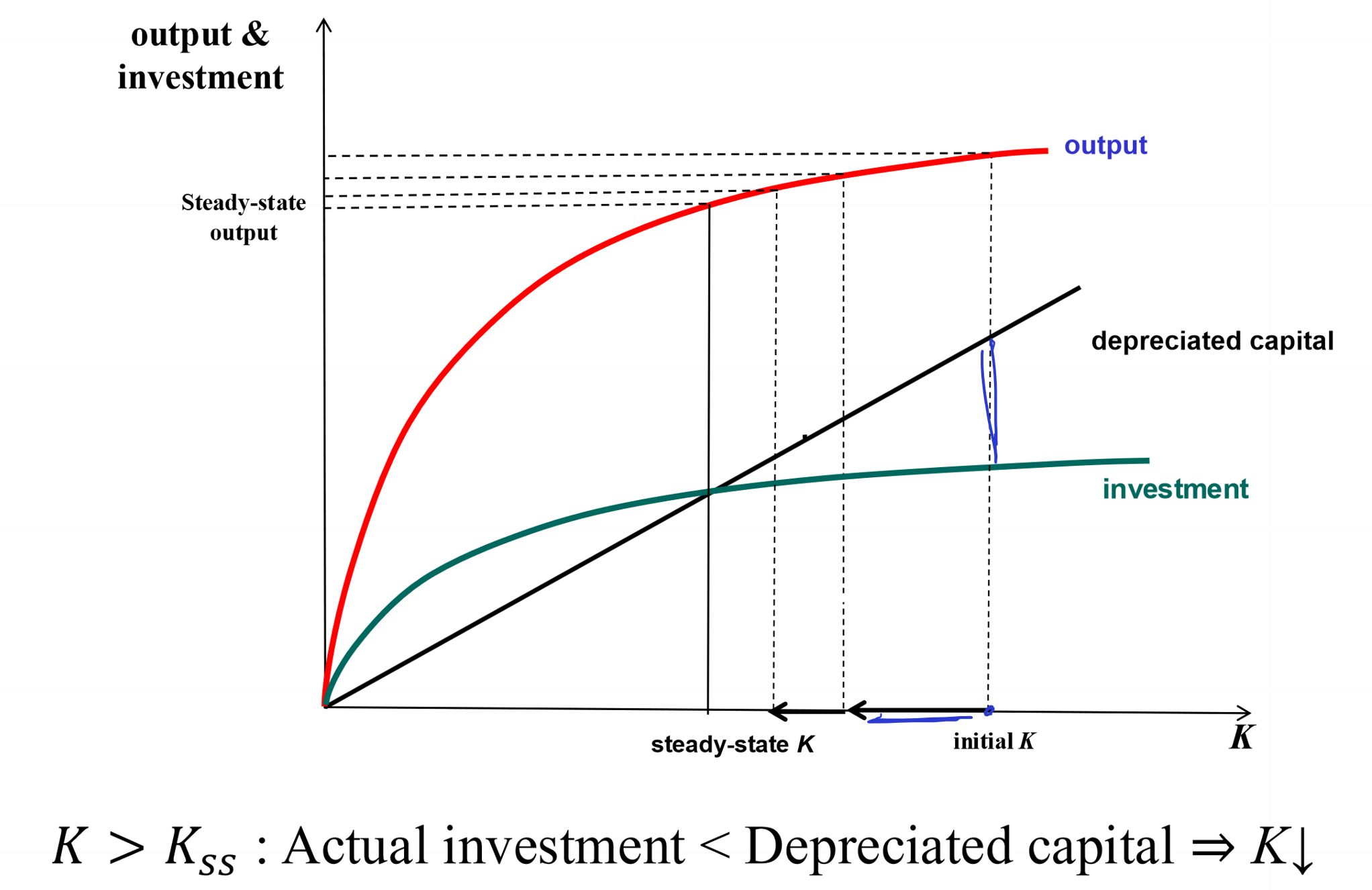
Starting above steady state

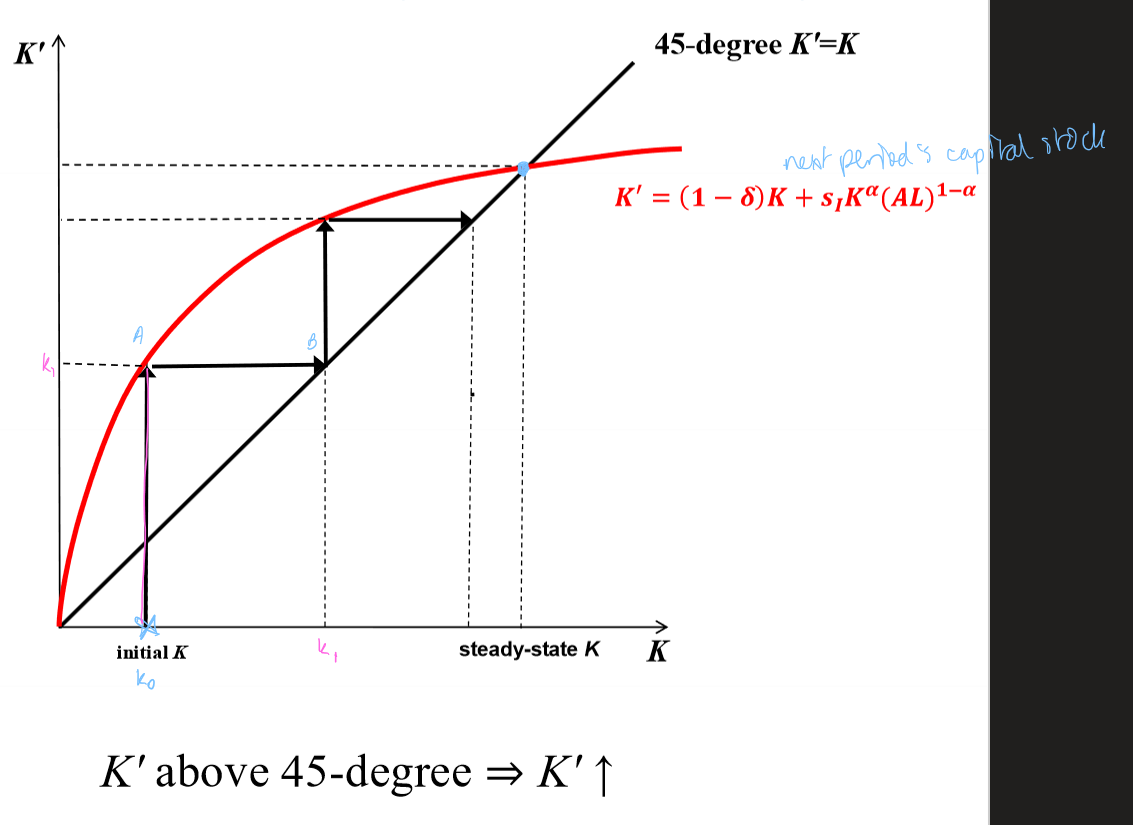
K,K’ space, when economy starts below steady state

Only works in discrete time

Key Implications Solow Model #1

Eventually no growth bc

• A is constant

• and diminishing returns

Growth higher for poor (ie low K) countries (conditional on having same A, sI , 𝛿)

Permanent Increase in sI - will they grow faster

If a country starts saving more permanently - will they grow faster

• in the end the growth is not higher because growth rate in the steady state is equal (rn it’s 0)

  • when add TFP growth and population growth, growth rate won’t be 0 but will still be 0 but will still be equal in two steady states

• during transition there is a temporary higher growth rate

  • dies out bc of diminishing returns to scale

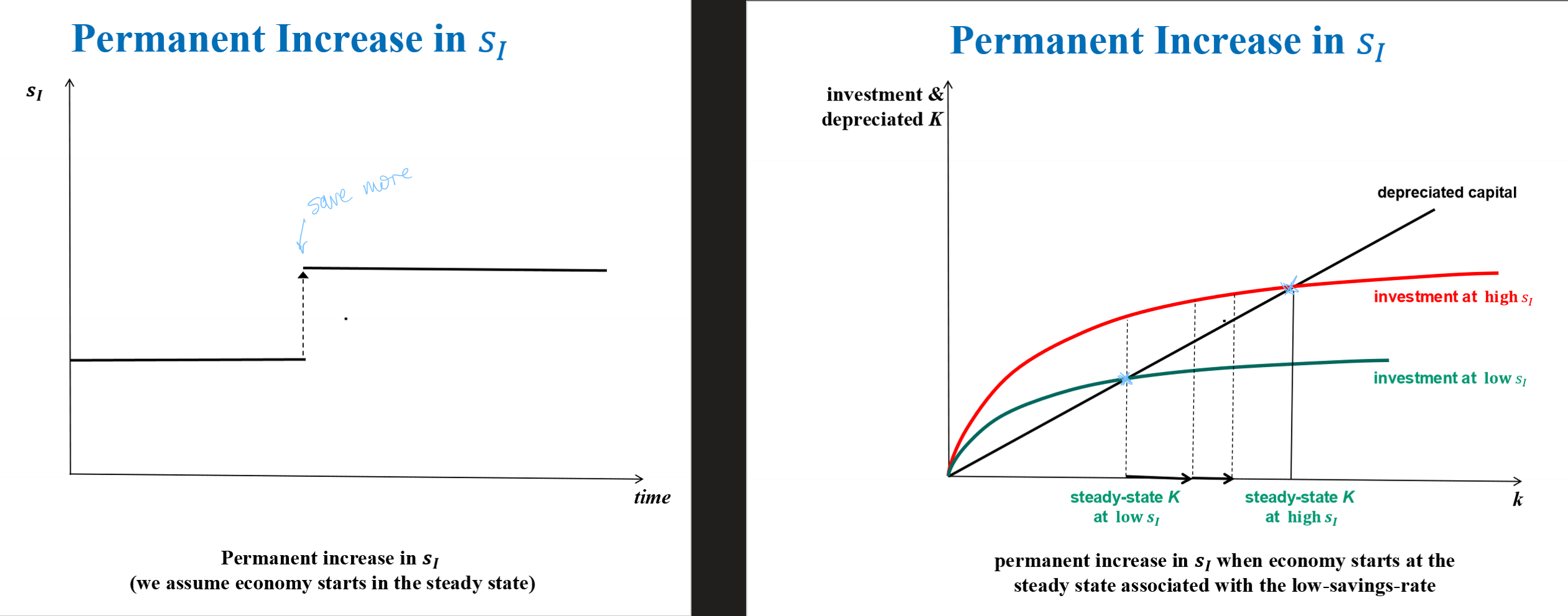
Key Implications Solow Model #2

Permanent increase in savings rate ⇒

• Higher steady-state per capita output level,

• Faster growth during transition,

• No permanent effect on growth

How does the Solow model and growth accounting explain China’s rapid growth, and what limits does it imply for future growth?

• China had a very high growth rate

• Growth was reinforced by structural transformation, with labour shifting from low-productivity agriculture to higher-productivity manufacturing.

• Very high savings rate

• Reforms expanded property rates

• Increased foreign investment

• Part of observed growth may be “recovery” because earlier events (e.g., the Cultural Revolution) temporarily destroyed/undermined the economy, so later growth partly reflects catching back up

• The Solow model implies that China cannot sustain high growth indefinitely through higher savings alone; as diminishing returns to capital set in, future growth increasingly depends on TFP growth.

Solow Growth Model: Successes

1. It can explain growth bursts after large destructions of capital/infrastructure,

   • e.g. in Germany and Japan after WWII.

2. It can at least partially explain growth bursts after countries increase savings rate:

   • fast growth of communist countries after WWII.

   • China’s growth and “growth miracle” of Asian Tigers (Hong Kong, Singapore, South-Korea and Taiwan).

3. It can explain GDP convergence for similar countries.

Solow Growth Model: Failures

4. It says nothing about TFP growth which we know is important.

• That is, it can only handle exogenous TFP growth.

5. It cannot explain the lack of GDP convergence that we also see in the data.

Is there convergence?

Yes if countries are similar

If Solow model is correct, then

• Low initial K (and Y) imply faster growth

• As Y increases, then subsequent growth should slow down

Poverty trap

• Solow Assumption: amount saved is a constant fraction of output.

• But saving rates are likely to be lower when income is low. (i.e., for poor countries).

• Model predictions can be quite different.

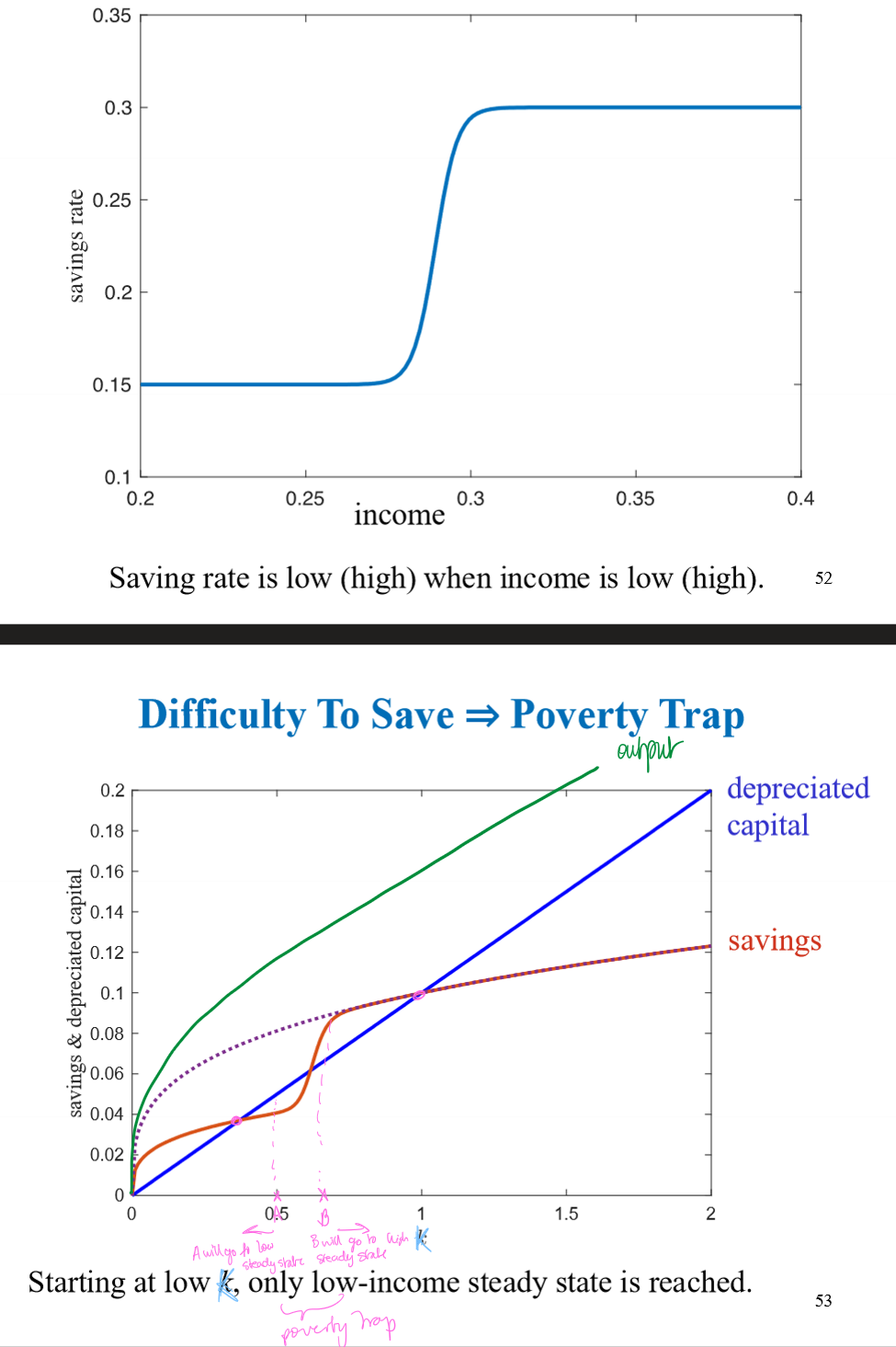
Poverty trap + Foreign Aid

The poverty trap model provides an explanation for why foreign aid has not been successful, namely foreign aid has simply not been large enough to push the country out of the bad steady state.

So, economists like Jeffrey Sachs have argued for a “Big Push” in terms of foreign aid

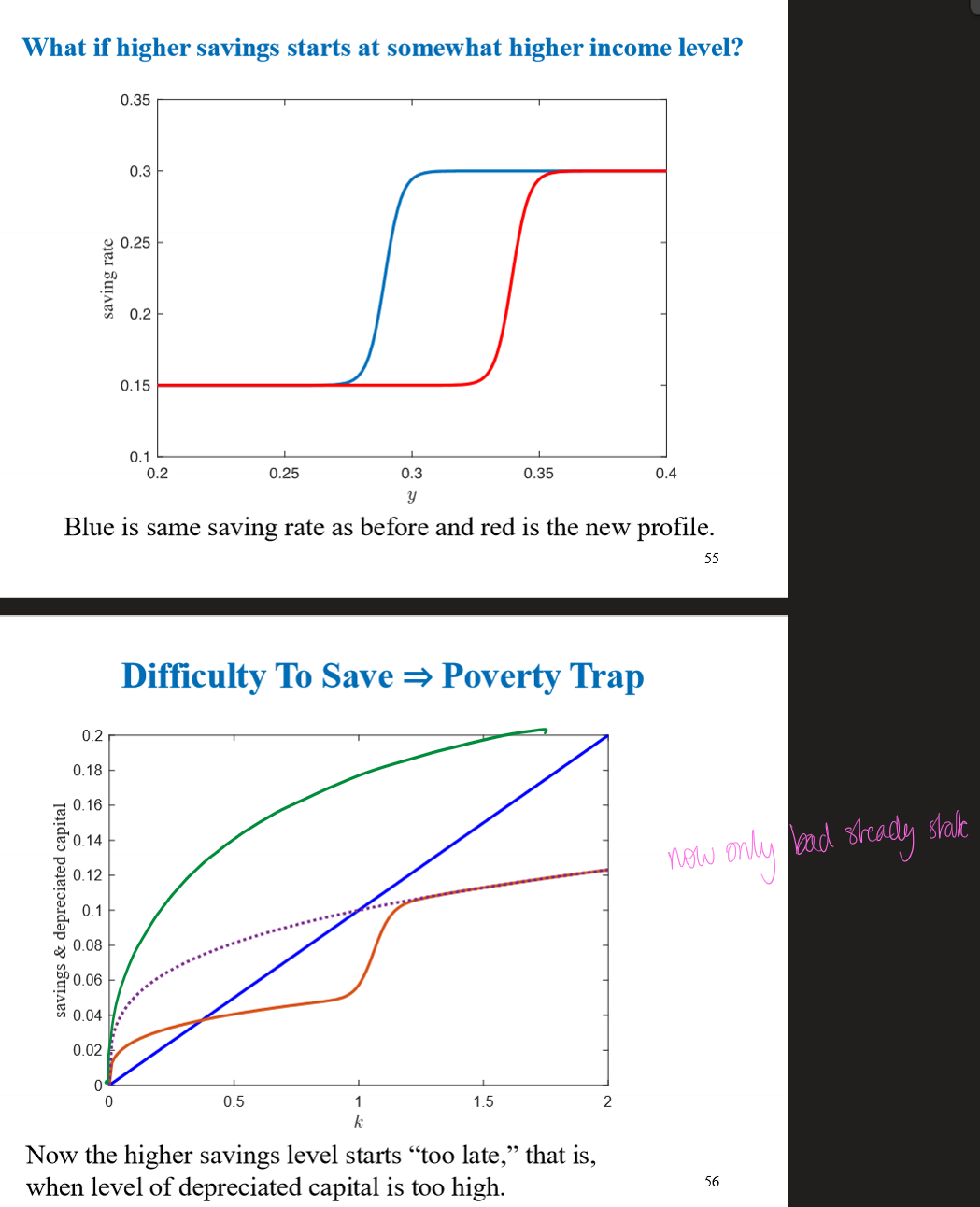
What if higher savings start at somewhat higher income level

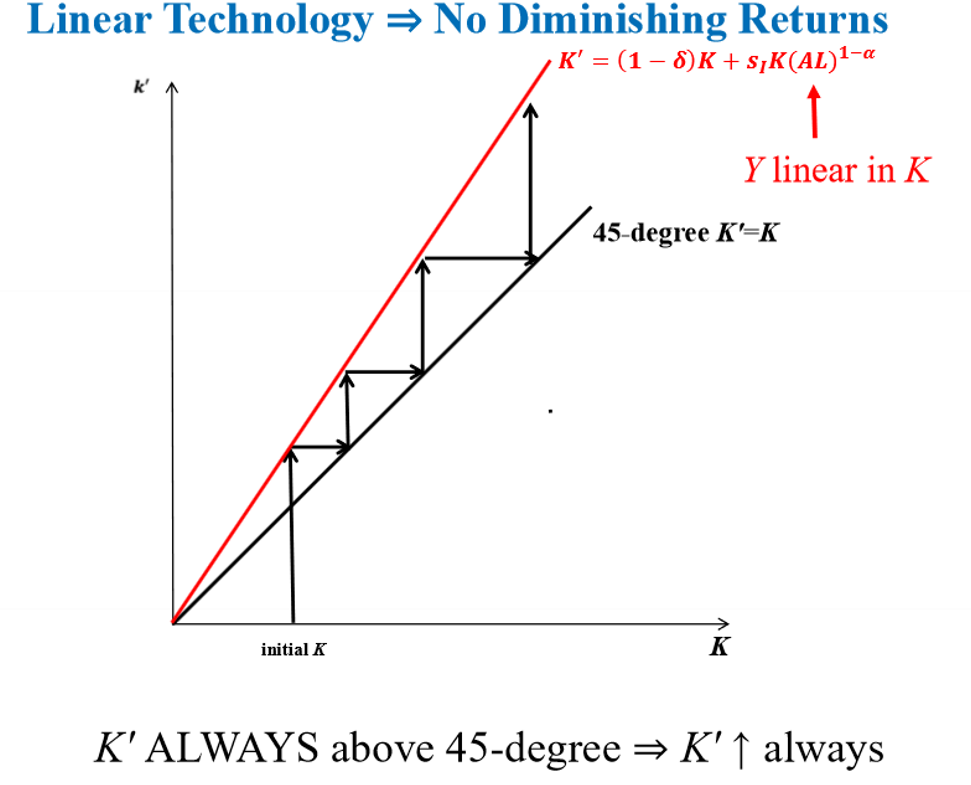
Why is decreasing returns to scale crucial in the Solow model, and what happens if technology is linear in capital?

• The assumption of decreasing returns to scale in capital is key for the Solow result that savings cannot generate long-run growth.

• If technology is linear in capital (no diminishing returns), output is linear in K.

• In this case, the capital accumulation equation implies K′ is always above the 45-degree line.

• Capital keeps increasing forever, so long-run growth through saving is possible.

• Therefore, diminishing returns are what prevent perpetual growth via capital accumulation in the standard Solow model.

What fundamental question does the Solow model raise, and how does the Romer model answer it?

• The Solow model raises the question: how does the real world overcome decreasing returns to scale?

• Without overcoming diminishing returns, sustained growth is impossible in Solow.

• The Romer model answers this by introducing permanent TFP growth.

• In the Romer model, TFP growth is endogenous, not exogenous.

Summary

• Growth accounting shows that both capital accumulation and TFP matter for economic growth.

• The Solow model implies:

  • Continued growth is not possible through high savings alone.

  • Sustained growth requires TFP increases.

  • A poverty trap can arise if the savings rate depends on income.

• The data show that:

  • The Solow model can explain specific growth episodes and countries.

  • Similar countries display convergence.

  • Many poor countries do not catch up