HGE Formulas 01

Hydraulics

Density

ρ = mass / volume

Density of Water

ρ_w = 1000 kg/m³ = 1.94 slugs/ft³

Specific Volume

ν = 1 / ρ = volume / mass

Weight

w = mg

Unit Weight

γ = w/v = mg / v

Unit Weight of Water and Air

γ_w = 9810 N/m³ = 62.4 lbs/ft³

γ_air = 12 N/m³

Specific Gravity

sg = γ / γ_w = ρ / ρ_w

Specific Gravity of Common Fluids

Freshwater: 1.00

Seawater: 1.03

Oil: 0.80

Mercury: 13.6

Glycerin: 1.25

Surface Tension: Pressure inside a Droplet

p = 4σ / d

p = gage pressure

σ = surface tension

d = diameter of droplet

Surface Tension: Capillary Rise

h = 4σ cosθ / γd

h = capillary rise or depression

θ = contact angle from vertical

d = diameter of tube

Viscosity

µ = τ / (dV / dy)

µ = viscosity

τ = shear stress

dV / dy = change in velocity wrt distance

Kinematic Viscosity

ν = µ / ρ

Compressibility

ß = (- dV / V) / dp = 1 / E_B

dV / V = change in volume

dp = change in pressure

E_B = bulk modulus of elasticity

Pressure

p = γh

p_B = p_A + γh

Pressure Head

h = p / γ

h_B = sg_A / sg_B × h_A

Absolute Pressure

p_abs = p_atm = p_gage

p_atm = 101.325 kPa = 1 atm = 760 mmHg = 760 torr = 14.7 psi

Gas Pressure (Absolute)

p = ρRT ; R = 287.4 Nm / kg K

p = γRT ; R = 29.3 m / K

T = Temperature in Kelvin (°C + 273 K)

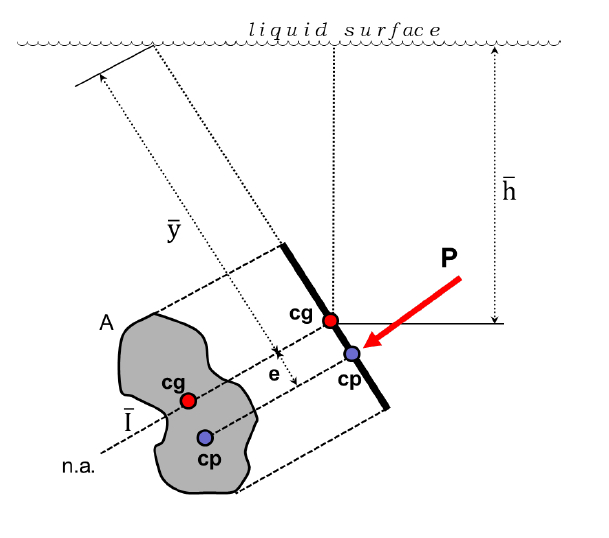
Hydrostatic Pressure: Plane Surface

P = γ × h-bar × A

e = I / Ay-bar

Location of Force: y-bar + e

h-bar = distance of the cg below the liquid surface “l.s.”, on the vertical

A = submerged area

e = distance of cp below the cg along the body

I = moment of inertia of A wrt centroidal axis

y-bar = distance of the cg below the liquid surface “l.s.”, on the vertical

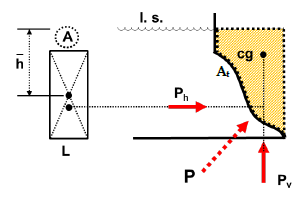
Hydrostatic Pressure: Curved Surface

Force = √(P_h² + P_v²)

P_h = γ × h-bar × A → Location same as plane surface

P_v = γ × A_t × L = γ × Volume → Location at the c.g. of volume

P_h = Horizontal Component

P_v = Vertical Component

A_t = Area traced above the curved projection until the liquid surface

Archimedes’ Principle

BF = γ_f × V_d

BF = buoyant force

γ_f = unit weight of displaced fluid

V_d = volume of fluid displaced (body immersed)

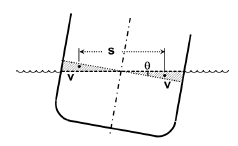
Distance of MB_o

Rectangular Sections: MB_o = B² / 12D × [1 + 0.5 tan² θ]

Other Sections (exact): MB_o = v s / (V sinθ)

Approximate: MB_o = I / V

θ = angle of tilting

v = volume of the wedge of immersion/emersion

s = horizontal distance between the centroids of v’s

I = moment of inertia of an area which is the top view of the body at the level of the liquid surface with respect to the axis of tilting

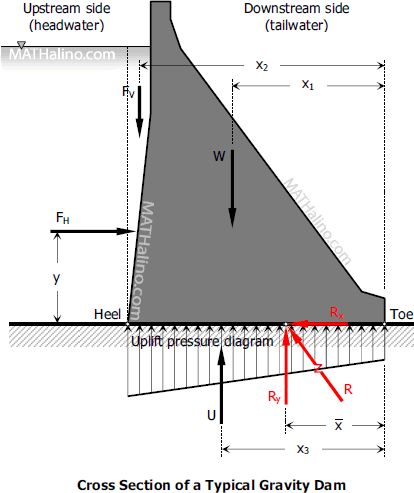
Dams: Factor of Safety against Overturning

FS_O = RM / OM

RM = Righting Moment

OM = Overturning Moment

Note: Take moments at toe

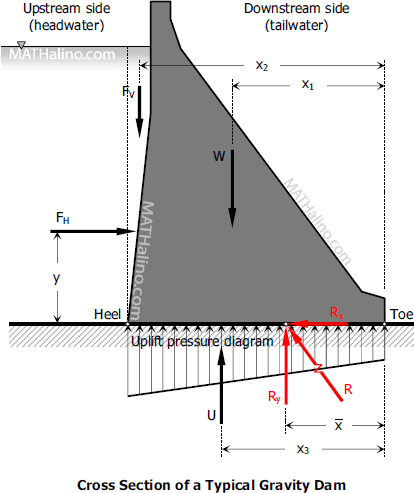
Dams: Factor of Safety against Sliding

FS_S = µR_y / R_x

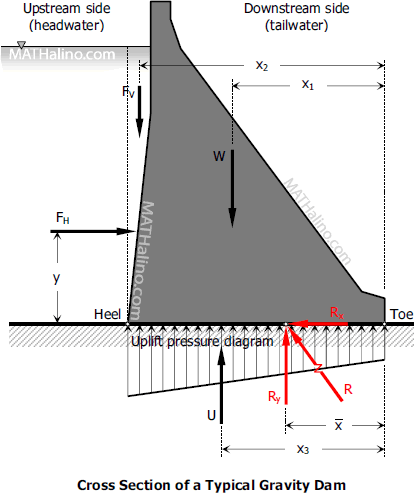
Dams: Location of R_y and e

x-bar = (RM - OM) / R_y

e = | B/2 - x-bar |

Dams: Foundation Pressure

If e ≤ B/6: q = R_y / B × (1 ± 6e / B)

If e > B/6: q_max = 2R_y / (3 × x-bar); q_min = 0

Hoop and Circumferential Stresses: Walls Carrying Stress in Pipes and Tanks

t = pD / 2S_t (eff)

t = thickness of the wall

D = inside diameter

p = unit pressure of fluid

St = actual or allowable tensile stress in the wall

eff = efficiency of the connections

Hoop and Circumferential Stresses: Hoops Carrying Stress in Pipes and Cylindrical Tanks

S = 2T / pD

S = center to center spacing of the hoops

T = tensile force in one hoop

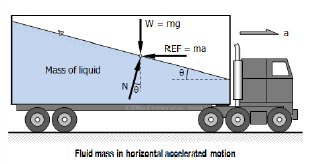
Moving Vessel: Horizontal Motion

tan𝜃 = a / g

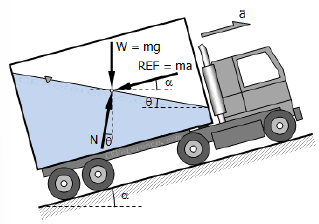
Moving Vessel: Inclined Motion

tan𝜃 = a_h / (g ± a_v)

Note: (+) = upward motion, (-) = downward motion

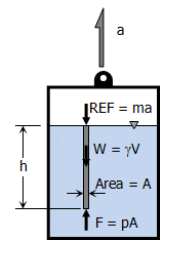
Moving Vessel: Vertical Motion

p = γh (1 ± a / g)

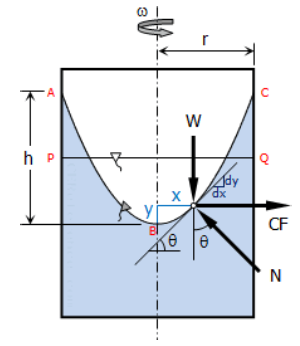
Rotating Vessel

tan𝜃 = ω² x / g

y = ω² x² / 2g

r² / h = x² / y

Note: 1 rpm = π/30 rad/sec

Fluid Flow: Discharge

Q = AV

A = cross-sectional area of flow

V = velocity of flow

Total Head/Energy

E = v² / 2g + p / 𝛾 + z

Velocity Head: v² / 2g

Pressure Head: P / 𝛾

Elevation Head: z

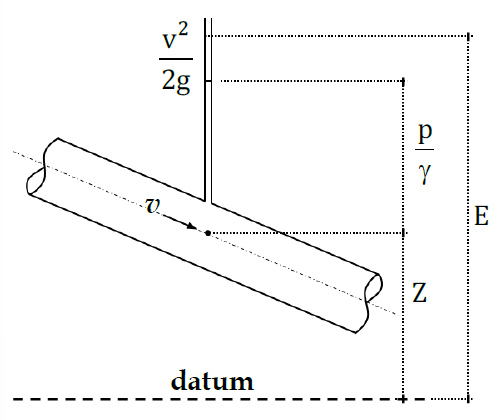
Bernoulli’s Principle of Fluid Flow

Theoretical: v₁² / 2g + p₁ / 𝛾 + z₁ = v₂² / 2g + p₂ / 𝛾 + z₂

Actual: v₁² / 2g + p₁ / 𝛾 + z₁ = v₂² / 2g + p₂ / 𝛾 + z₂ + HL

w/ Pump or Turbine: v₁² / 2g + p₁ / 𝛾 + z₁ + HA = v₂² / 2g + p₂ / 𝛾 + z₂ + HL + HE

HL = head loss

HA = head added by pump

HE = head extracted by turbine

Slope of EGL

S = HL / L

Power of Pump or Turbine

P = Q 𝛾 E

E = HA (pumps) or HE (turbines)

Efficiency of Pump/Turbine

Eff = Output / Input

HA - Output

HE - Input

Head Loss: Darcy-Weisbach

General Formula: h_f = fL / D × v² / 2g

Circular Pipes: h_f = 0.0826fL Q² / D⁵

Head Loss: Manning Formula

General Formula: h_f = 6.35 n²L v² / D^4/3

Circular Pipes: h_f = 10.29 n²L Q² / D^16/3

Head Loss: Hazen-Williams Formula

General Formula: v = 0.8492 C R^0.63 S^0.54

Circular Pipes: h_f = 10.67LQ^1.85 / (C^1.85D^4.87)

Hydraulic Radius for non-circular pipe

R = A / P

D = 4R

Note: P = wetted perimeter

Minor Head Loss

h_m = k_m v² / 2g

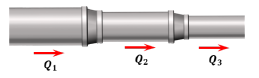
Pipes in Series

Q₁ = Q₂ = Q₃

HL = h_f1 + h_f2 + h_f3

h_f = Δp / γ

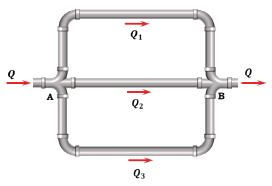
Pipes in Parallel

Q = Q₁ + Q₂ + Q₃

h_f1 = h_f2 = h_f3

Celerity for rigid pipes

c = √(E_B / ρ)

Celerity for Non-Rigid Pipes

c = √(E_C / ρ)

1/E_C = 1/E_B + d/Et

d = internal diameter of pipe

E = modulus of elasticity of pipe material

t = pipe thickness

Water Hammer: Time required for the pressure wave to travel from the

valve to the reservoir and back to the valve is:

T = 2L / c

Water Hammer Pressure

Rapid Closure (t_c < 2L/c): P_h = ρcv

Slow Closure (t_c > 2L/c): P_h’ = 2Lρv/t_c

Reynold’s Number

N_R = VD / ν

V = velocity of flow

D = diameter of pipe

ν = kinematic viscosity

Friction Factor given Reynold’s Number

N_R < 2000: f = 64 / N_R

N_R > 2000: 1 / √f = -2log(ε / 3.7D + 2.51 / N_R√f)

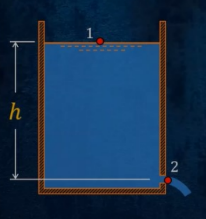
Torricelli’s Formula for Orifice

Theoretical: v₂ = √2gh

Actual: v = C_v√2gh

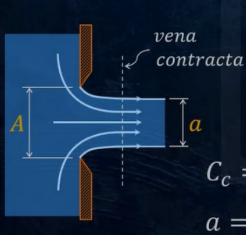
Orifice: Vena Contracta

Cc = a/A

C = C_c C_v

Q = av = C_cC_vA√2gh = CA√2gh

HL = v² / 2g × (1 / C_v² - 1)

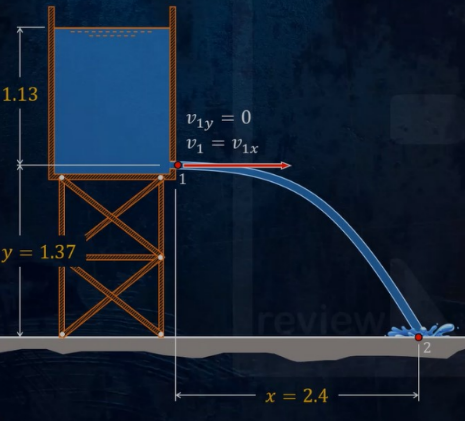
Projectile of Orifice

x = v_1x t

y = v_1y t - ½ gt²

v_2y² = v_1y² - 2gy

y = xtanθ - gx² / (2v₁² cos²θ)

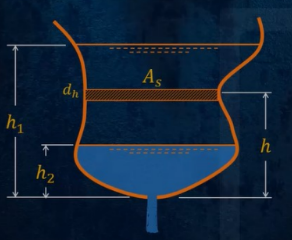
Falling Head: Orifice

General Formula: t = ∫ A_sdh / CA√(2gh) from h₂ to h₁

Constant A_s: t = 2A_s / (CA√2g) × (√h₁ - √h₂)

Open Channel: Discharge and Velocity

Q = Av

v = C√RS (Chezy Formula)

Chezy Coefficient

Theoretical: C = √(8g / f)

Manning: C = 1/n × R^1/6

Bazin: C = 87 / (1 + m/√R)

Note: m and n are roughness coefficients

Kutter’s Formula

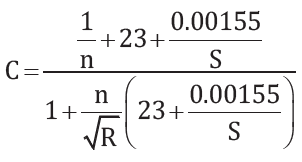
Chezy-Manning Formula

v = 1/n × R^2/3 × S^1/2

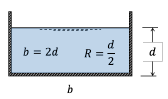
Open Channel: Most Efficient Rectangular Section

b = 2d

R = d/2

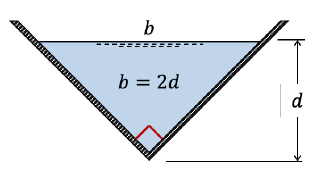
Open Channel: Most Efficient Triangular Section

b = 2d

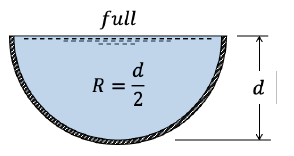
Open Channel: Most Efficient Semicircular Section

channel is full; R = d/2

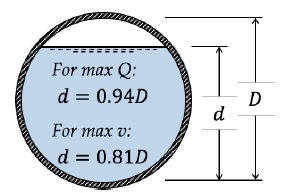
Open Channel: Most Efficient Circular Section

Max Q: d = 0.94D

Max v: d = 0.81D

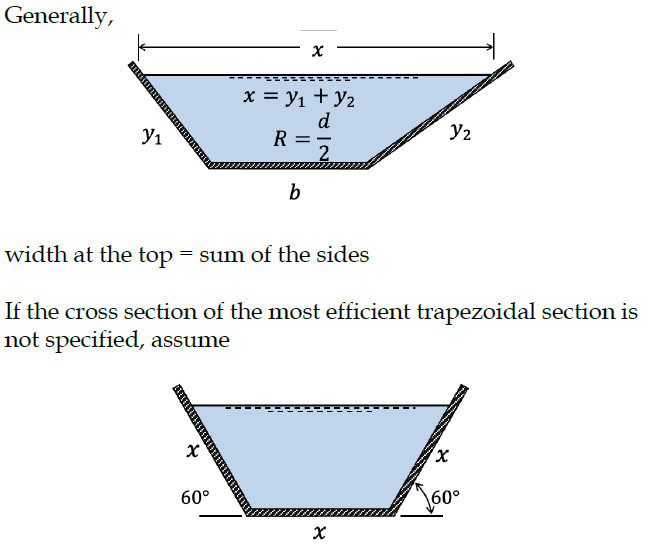
Open Channel: Most Efficient Trapezoidal Section

For given cross-section: x = y₁ + y₂ and R = d/2

For cross-section not specified: x = y₁ = y₂ (half regular hexagon)

Froude Number

N_F = v / √gd_m

d_m = average depth = A/B

B = width of liquid surface

Critical Depth

Q² / g = A_c³ / B_c ; q = discharge per meter width

Rectangular Sections:

• d_c = ³√q² / g

• d_c = 2/3 × E_c; E_c = v_c² / 2g + d_c

Critical vs. Subcritical vs. Supercritical Flow

Critical: N_F = 1

Subcritical: N_F < 1

Supercritical: N_F > 1

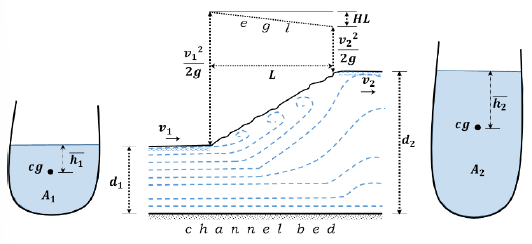
Hydraulic Jump

Power lost = Qγ(HL)

P₂ - P₁ = Qγ/g (v₁ - v₂)

Rectangular Section: q² / g = d₁ d₂ (d₁ + d₂) / 2

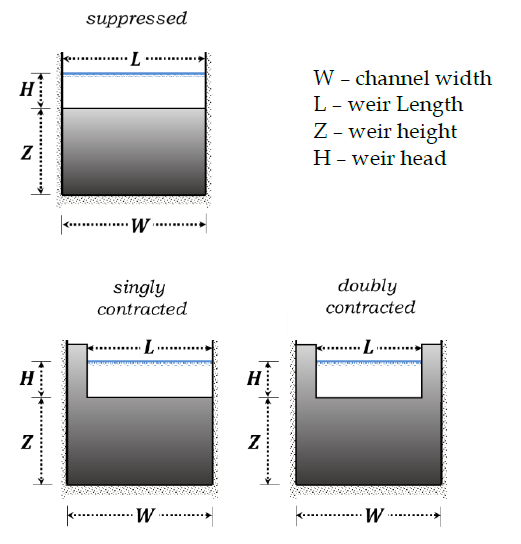
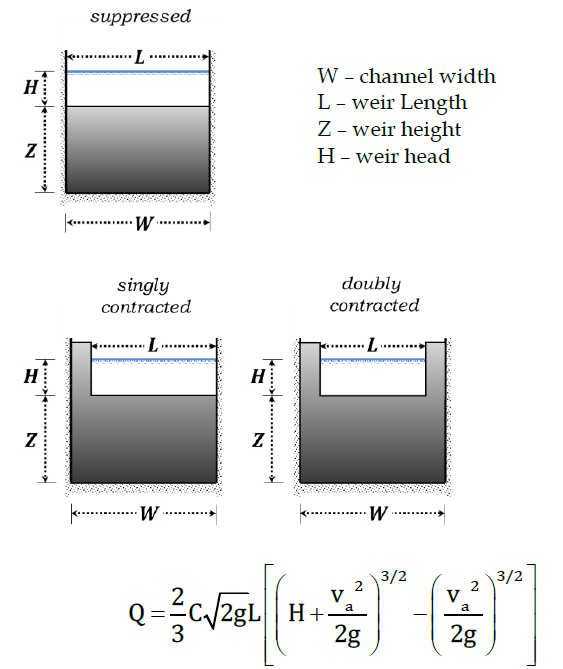
Rectangular Weir

Q = mLH^3/2 or Q = 1.84LH^3/2 (Francis formula)

For contracted sections:

L’ = L - 0.1H (singly contracted)

L’ = L - 0.2H (doubly contracted)

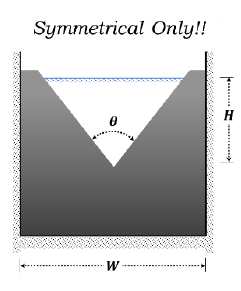
Triangular Weir

Q = 8/15 × C√2g × tan(θ/2) × H^5/2

Q = 1.4H^5/2 for θ = 90°

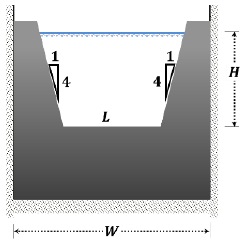
Cipolletti Weir

Q = 1.86LH^3/2

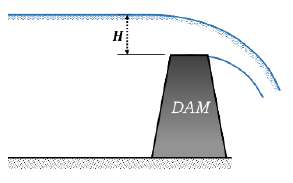
Broad-Crested Weirs (Dams)

Q = 1.71LH^3/2

L = length of dam

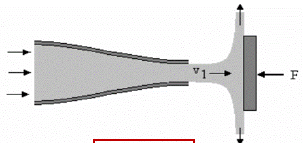
Impact of a Jet on a Plane/ Force on the Jet

F = ρQv

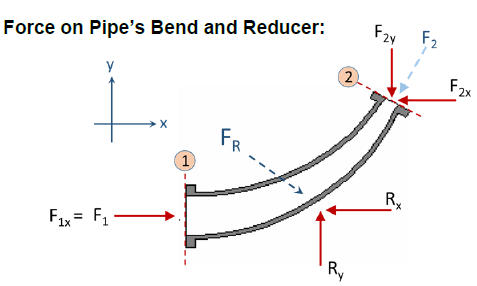
Force on Pipe’s Bend and Reducer

ΣF_x = ρQ (v_2x - v_1x)

ΣF_y = ρQ (v_2y - v_1y)

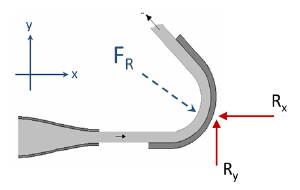
Force on a Curved Vane/Blade

ΣF_x = ρQ (v_2x - v_1x)

ΣF_y = ρQ (v_2y - v_1y)