Calculus AB Golden Notes
4.6(10)
4.6(10)
Card Sorting
1/101
Earn XP
Description and Tags
Everything you need to know & understand for the AB calculus exam
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
102 Terms
1
New cards
Derivative Power Rule
If f
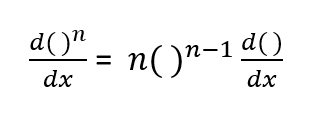
2
New cards
Derivative exponential rule
\
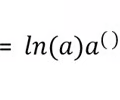
3
New cards
Derivative e Rule
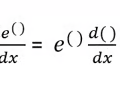
4
New cards
Derivative Ln Rule
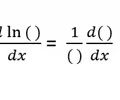
5
New cards
Derivative Square Root Rule
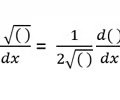
6
New cards
Derivative Tangent Rule
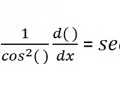
7
New cards
Derivative Sine Rule
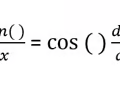
8
New cards
Derivative Cosine Rule
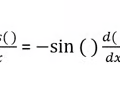
9
New cards
Derivative Inverse Sine Rule
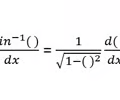
10
New cards
Derivative Inverse cos rule
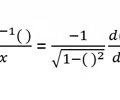
11
New cards
Derivative Inverse tan rule
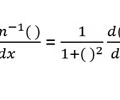
12
New cards
Derivative constant Rule
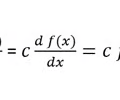
13
New cards
Derivative Chain Rule
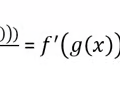
14
New cards
Derivative Product Rule
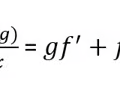
15
New cards
Derivative Quotient Rule
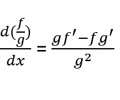
16
New cards
Derivative Addition Rule
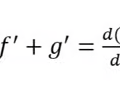
17
New cards
Anti-derivative power rule
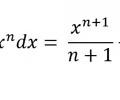
18
New cards
Anti-derivative expanded power rule
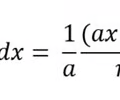
19
New cards
Anti-derivative exponential rule
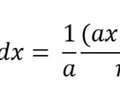
20
New cards
Anti-derivative expanded exponential rule
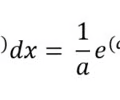
21
New cards
Anti-derivative Ln Rule
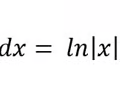
22
New cards
Anti-derivative Ln expanded rule
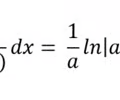
23
New cards
Anti-derivative sine rule
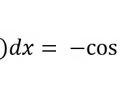
24
New cards
Anti-derivative expanded sin rule
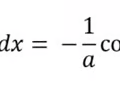
25
New cards
Anti-derivative cos rule
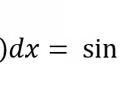
26
New cards
Anti-derivative expanded cos rule
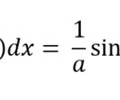
27
New cards
Derivative of inverse f(x)
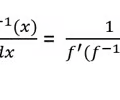
28
New cards
Displacement
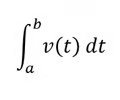
29
New cards
Total Distance
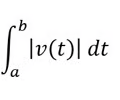
30
New cards
Derivative of an integral
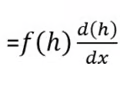
31
New cards
Differentiable if
continuous, no corner or vertical tangent
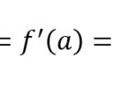
32
New cards
Continuous if
No removable discontinuity, jumps, or vertical asymptotes.
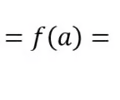
33
New cards
Limits if x-\>∞ then
1. compare terms that add
2. Factor & divide
3. Left & Right
4. L'hopital's rule
2. Factor & divide
3. Left & Right
4. L'hopital's rule
34
New cards
Place in order of growing fastest as x -\>∞:
x^99, e^x, lnx
x^99, e^x, lnx
lnx, x^99, e^x
35
New cards
Find the average value of f(x)
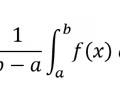
36
New cards
Find the average rate of change
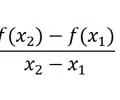
37
New cards
v(t) is the
rate at which x is changing; tangent slope; instantaneous rate of change
38
New cards
Average value of f'(x) is the same as
average rate of change
39
New cards
secant slope is the
average rate of change
40
New cards
Find the secant slope
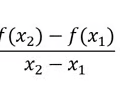
41
New cards
e^(lnA)
A
42
New cards
lne^A
A
43
New cards
e^(A+B)
e^Ae^B
44
New cards
ln12-ln4
ln(12/4)
45
New cards
f(x) has a critical point when
f'(x)\=0 or f'(x)\=undefined
46
New cards
Min-Max Theorem
The absolute Max/Min of f(x) is at the beginning of f(x) at the end of f(x) or at a critical point on f(x)
47
New cards
f(x) has an inflection point when
f(x) changes concavity, OR f'(x) changes I to D or D to I or when f"(x) changes sign
48
New cards
L'Hopitals Rule
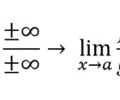
49
New cards
The limit exists if
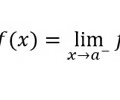
50
New cards
Area of a semicircle
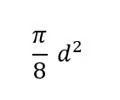
51
New cards
Solve an Equation
Find value which makes equation true OR graph both halves of equation & find intersection
52
New cards
The particular solution y\=B(t) of a differential equation dB/dt\=1/5(100-B) with initial condition B(0)\=20 what would you use?
Use SACI
53
New cards
SACI
Separate, Anti Differentiate, Constant-tate, Isolate
54
New cards
Speed is increasing when
v(t) and a(t) are the same sign
55
New cards
Approximate the instant rate of change by:
calculating the average rate of change
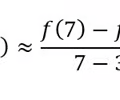
56
New cards
Approximate the tangent slope by:
calculating the nearest secant slope
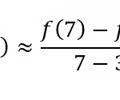
57
New cards
When the in rate is E(t) and the out rate is L(t) what is the equation for the rate?
A'(t)\=E(t)-L(t)
58
New cards
Solve an anti-derivative
1. Rule 2. u substitution 3. Algebra trick
59
New cards
Average rate of change of velocity is the same as
average acceleration
60
New cards
average rate of change of position is the same as
average velocity
61
New cards
secant slope is the same as
average rate of change of f(x)
62
New cards
secant slope or average roc or f(x)
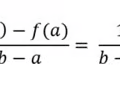
63
New cards
average roc of x(t) or average velocity
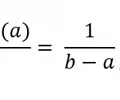
64
New cards
average roc of v(t) or average acceleration
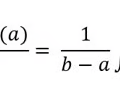
65
New cards
speed
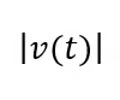
66
New cards
F'(x)\=
f(x)
67
New cards
anti-derivative of f(x)
F(x)
68
New cards
anti-derivative of f'(x)
f(x)
69
New cards
integral from a to b of a(t) equals
v(b)-v(a)
70
New cards
integral from a to b of v(t) equals
x(b)-x(a)
71
New cards
integral from a to b of f(x) equals
F(b)-F(a)
72
New cards
integral from a to b of f'(x) equals
f(b)-f(a)
73
New cards
integral of a rate equals
change in amount
74
New cards
Mean Value Theorem
If f(x) is continuous and differentiable the "tangent slope at c" \= secant slope
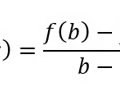
75
New cards
Tangent line formula
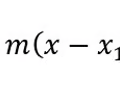
76
New cards
If f(x) is concave down the tangent line is
an OVER approximation
77
New cards
If f(x) is concave up the tangent line is
an UNDER approximation
78
New cards
Trapezoidal riemann sum formula
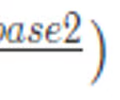
79
New cards
f'(x)\=dy/dx\= Formula to find:
1. Instantaneous rate of change of f(x)
2. Slope of line tangent to f(x)
3. Slope of f(x) at a point
4. Instant rate at which f(x) is changing
2. Slope of line tangent to f(x)
3. Slope of f(x) at a point
4. Instant rate at which f(x) is changing
80
New cards
f(x) has relative/local max when
f'(x) changes + to - or when f"(x) changes I to D
81
New cards
lne^2
2
82
New cards
lne
1
83
New cards
lne^0
0
84
New cards
ln1
0
85
New cards
ln(1/e)
-1
86
New cards
lne^(-1)
-1
87
New cards
ln(1/e^-2)
-2
88
New cards
rate of change of position
x'(t) or v(t)
89
New cards
rate of change of velocity
v'(t) or a(t)
90
New cards
Vertical Tangent when
number/0
91
New cards
Jump discontinuity when
the left limit is different from the right limit
92
New cards
Removable discontinuity when
the value is different than the limits on the left and right. Limits must be the same on left and right.
93
New cards
Horizontal asymptote
the value of the limit as x-\>infinity
94
New cards
When given a rate and then asked to find the amount use
Fundamental Theorem
95
New cards
When given a rate that includes the output variable and then asked to find the amount use
SACI
96
New cards
f has an inflection point when
f changes concavity
97
New cards
f has a relative or local max when
f changes from increasing to decreasing
98
New cards
f has a relative extrema when
f changes from I to D or D to I or when f' changes + to - or - to +
99
New cards
f has a critical point when
the slope of f is 0 or undefined or when f' has a y-coord. of 0 or und
100
New cards
tangent slope means
instantaneous rate of change