Standardization

Bias:

systematic error in design or conduct of study that leads to incorrect estimate of association

• can be caused by investigator or study participants during design or conduct of study

• can occur in experimental, cohort, case-control, and other studies

• few studies have no bias or errors

What are the effects of bias?

creates appearance of an association when there is none, or mask an association that really exists

• selecting and information bias cannot be fixed in the analysis; confounding can be fixed…to a point

Crude rate:

total # of events divided by total # in population

• unstandardized

Standardized (adjusted) rate:

rate that is adjusted for a characteristic (e.g. age-standardized rates) and is used to indicate how overall rates would have compared if the populations had the same distribution of characteristics

• direct and indirect standardization

Crude data:

rate/risk is based on raw data

Crude All-Cause Mortality Rate:

total number of deaths from all causes per 100,000 population

• over specified time period

Crude Morbidity Rate for a Specific Disease:

number of cases of a disease per 100,000 population

• over specified time period

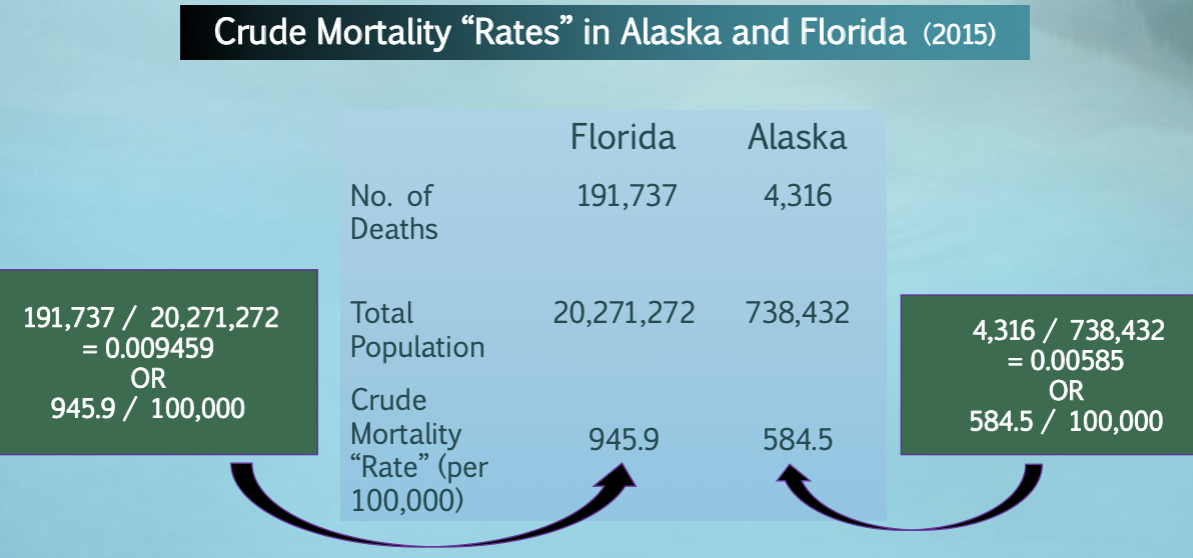
What if we wanted to compare crude rates?

we can conclude that crude mortality “rate” in Florida is much higher than the crude mortality “rate” in Alaska

• but does that mean that the risk of death is truly higher in Florida?

• the state populations differ with respect to underlying characteristics that affect overall death rate, and so we may be making an unfair comparison

Standardizing is a way to what?

is a way to control for confounding factors

What is the problem with comparing specific rates?

its cumbersome to compare five pairs of numbers and its not entirely clear which state has higher mortality

• one age-specific “rate” is higher in Florida

• four age-specific “rates” are higher in Alaska

What is the solution when comparing specific rates?

create a single number for each state that adjusts for age differences

• age-adjusted rates

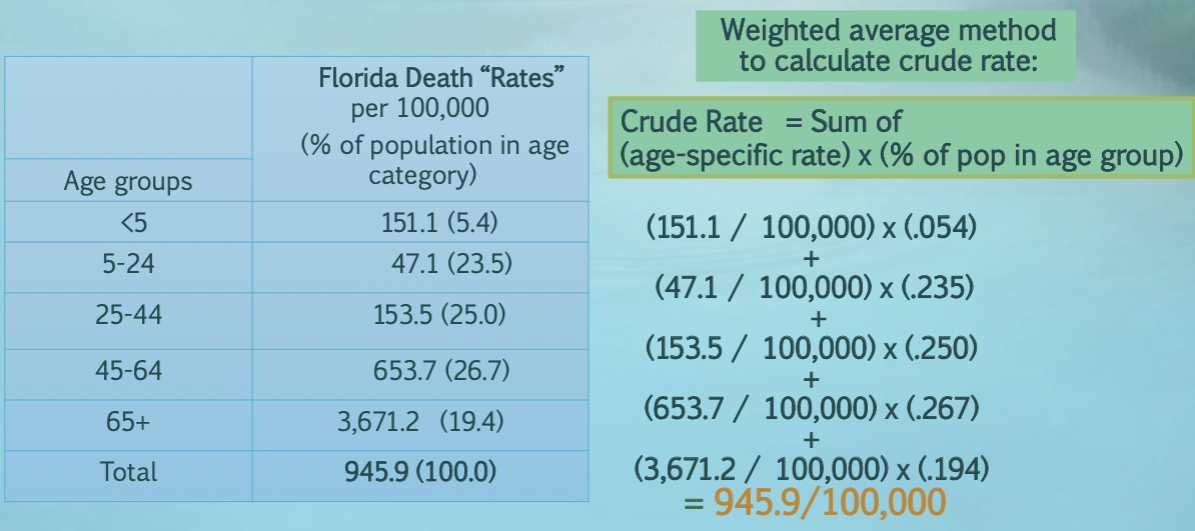
What is another way to calculate crude rates?

take the weighted average of age-specific rates, with weights equal to the proportion of the population in each category

How do we interpret age-adjusted rates?

adjusted rates are good only for comparison -- alone they are meaningless

• the remaining difference between the two adjusted rates is not due to age

• actual numbers will depend on the standard that is used

Direct standardization:

use when factor specific rates are known for both populations and calculate using population rate of disease and a standard distribution

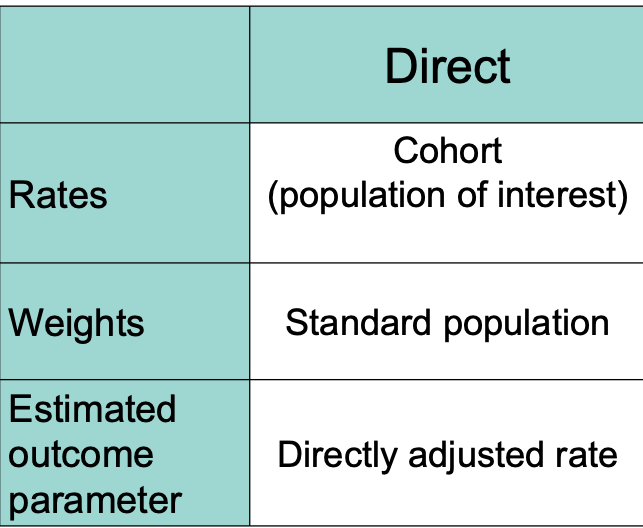
Summary of direct standardization:

provides summary rate that removes unwanted (usually age) differences between populations

• less cumbersome than comparing many specific rates

• however, adjusted rates are not real...their numeric value depends on the standard

• thus, they are only good for comparison