Computational thinking, algorithms and data representation

Computational thinking refers to a way of approaching problems that is particularly useful in computing. It can also be useful for tackling many other kinds of problems

What is computational thinking

Abstraction refers to the process of finding similarities or common aspects between problems and identifying differences and details that don't matter for the task at hand.

What is abstraction

strategies for simplifying a problem or for guiding an investigation

What are heuristics?

A sequence of steps required to solve a problem

What is an algorithm?

Abstraction refers to the process of finding similarities or common aspects between problems, and identifying differences and details that don't matter for the task at hand

What is abstraction?

Decomposition involves breaking down a large task into a set of smaller tasks

What is decomposition?

It can save time, and lead to more elegant solutions

What are two ways in which identifying patterns can help us to solve problems in computing.

Elegance refers to how desirable the algorithm is. Specifically how fast, and accurate it is. For example if an algorithm could produce a correct answer, extremely quickly, 99% of the time, it would be extremely elegant.

In relation to algorithms, what does 'elegance' refer to

Computers are so complex, that it is impossible for the average person to understand every single detail of how they work.

Why is abstraction necessary in computing?

When defining functions

When can we use abstraction when designing programs?

You don't need to know exactly how an argument operates, e.g., print(), as long as you understand how it works

Explain how functions can be used to achieve abstraction

A sequence of steps required to solve a problem

What is an algorithm

Be unambiguous

Consist of a finite number of steps

Have a clear flow of control from the beginning of the algorithm to the end

Algorithms for computers must meet additional criteria than non-computational computer works, what are they?

A mix of programming language and normal/everyday language used to describe instructions in a program less formally than using a programming language alone

What is pseudocode?

To represent the instructions in an algorithm in such a way that they can be executed by a computer

What is the purpose of a computer program in relation to an algorithm

Best case: When there is the least amount of work

Worst case: When there is the most amount of work

What is the difference between worst-case scenarios and best-case scenarios in an algorithm, with respect to the work done?

This is the option that requires the most time and is therefore the most conservative

Why do computer scientists tend to base estimates of work done by an algorithm on the worst-case scenarios?

Algorithmic time complexity is a measure of how long an algorithm would take to complete, given input n

What does algorithmic time complexity mean?

Time

What is the only factor that computer scientists consider when looking at algorithmic complexity?

When the amount of work done is linearly proportional to the input size n

What is meant by 'Linear complexity'

The special notation for describing algorithmic time complexity

What is meant by Big O notation

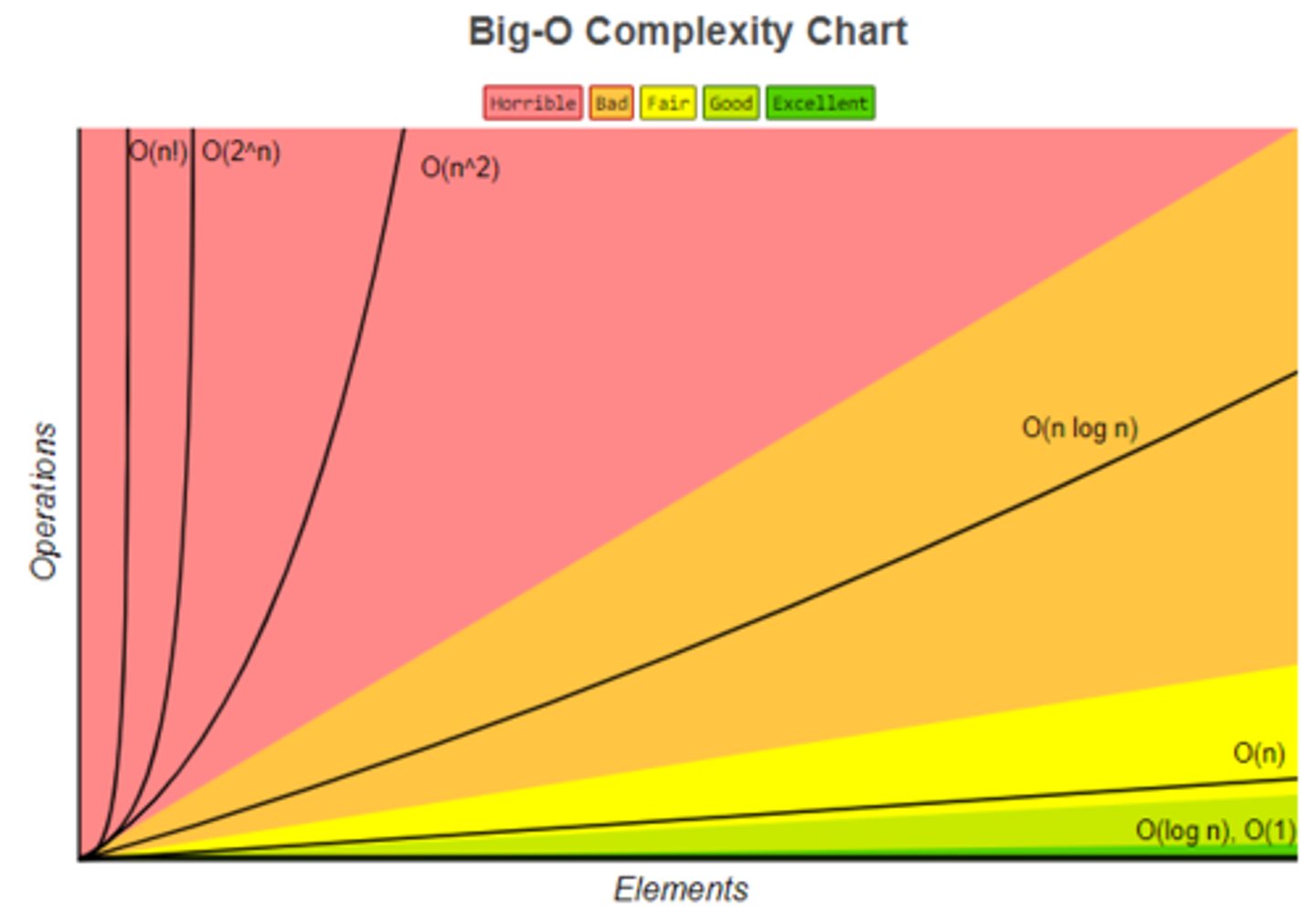
Equivalence classes group algorithms that have an equivalent (more or less) complexity.

What are equivalence classes of algorithms?

A linear search, which runs in 0(n) time

What does 0(n) class represent?

An algorithm that only looks at the first item in a data set

What does 0(1) class represent?

A quadratic algorithmic complexity, one that grows in proportion to the square of the input size. So if n=8 then the output = 64

What does 0(n^2) class represent?

They allow us to see which algorithms are in the same class

They allow us to quantify the difference in complexity

Equivalence classes can prevent computer scientists from wasting time looking for better algorithms that don't exist, as they can often be proven mathematically.

Why are equivalence classes are so important?

Linear search algorithm

Give an example of an algorithm that belongs to the 0(n) class

The highest order of 'n'

In relation to algorithmic complexity, what is considered to be a 'dominant term'.

Problems that no algorithm can solve in a reasonable amount of time, for example the travelling salesman

Explain what is meant by 'intractable' problems

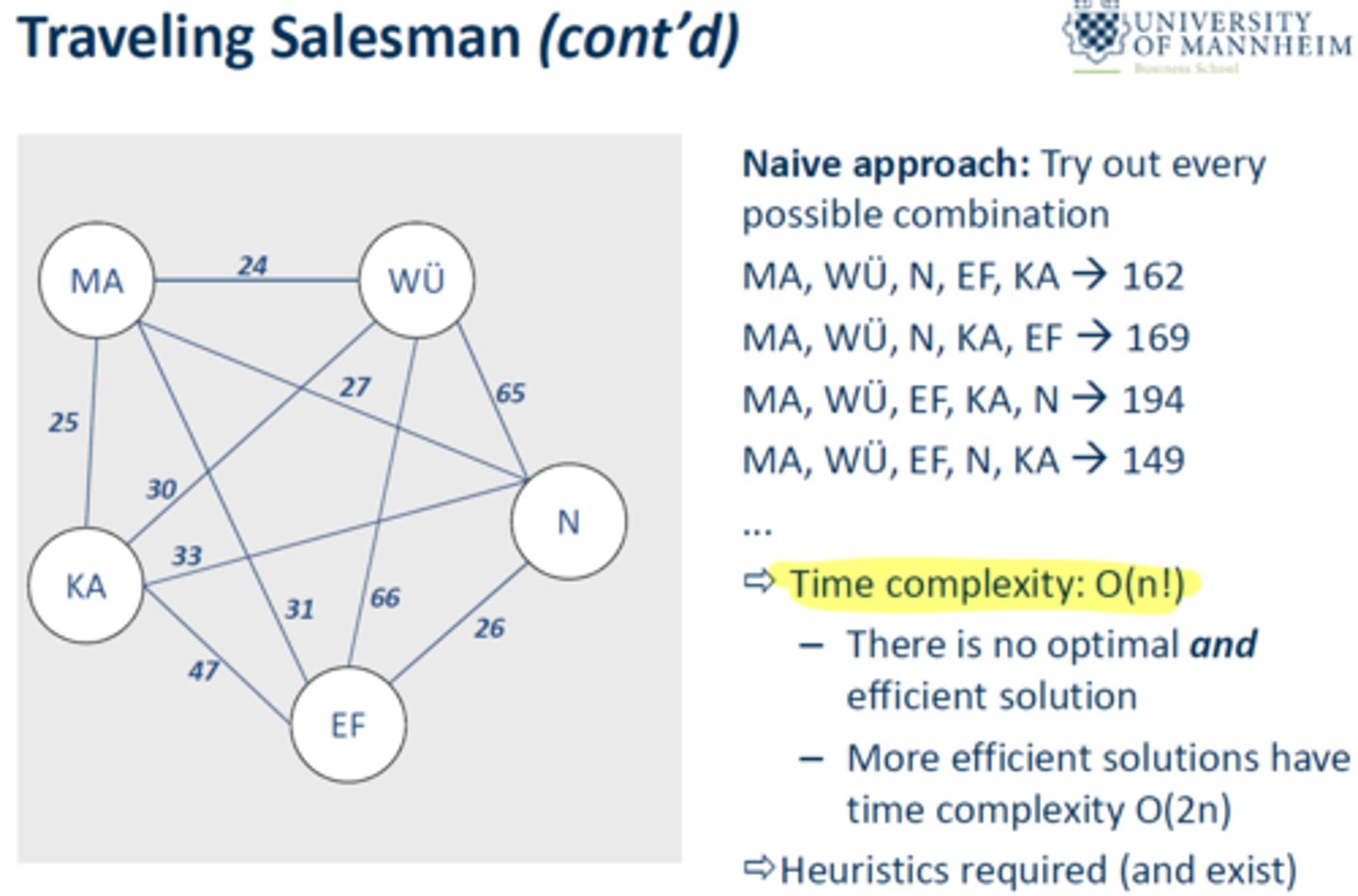
A rule of thumb which allows us to produce an approximate, yet usable solution to a problem

What is heuristic, in the non-computer sense?

When one needs a solution to an intractable problem?

When are heuristics useful?

The accuracy of a solution ma not always be known

Some heuristics may make assumptions about the original problems that may not be fair or appropriate.

What are two problems associated with solutions based on heuristic algorithms

When the problem is fully understood, and the consequences of any assumptions can be known and preferably quantified.

Under what circumstances are heuristics best applied?

Analog data, in other terms, data that has more than two values (0 and 1), e.g, the amount of numbers between 0 and 1 (infinite)

What is a continuous signal?

Digital data, in other terms, data that has only two values, 1 or 0 (ON/OFF)

What is a discrete signal?

The selecting of a subset of data, from the a larger data set/population

What does sampling refer to?

Some information is lost, as a digital signal can only form approximations from a continuous signal, for example 4.4 becomes 4

What is the 'trade-off' in sampling?

It is much easier to transport, store and copy than the analog alternative.

What are the advantages of storing information in digital format?

8

How many bits are in a byte?

1111 1111 or 255

What is the largest value that can be stored by a byte in binary and decimal?

256 different characters (2^8)

How many characters total can be stored in a byte?

1024 (1024 is the holy number in units of storage, only bits and bytes are the exception)

How many megabytes are there in a gigabite?

a) (2^40)

b) (2^50)

How many bytes are there in a terabyte (a), and a petabyte (b)

1000 0001 the 1's respectively from left to right are: Most important, and least important

Using an example of a binary, label the most and least important bit

2^0, or 1

What is the first place value in a binary number?

It's place value

What does the position of each bit in a byte represent?

Simplicity, can be carried out quickly by a computer

State two benefits of using binary numbers in computers

NOT

&

AND

What are the names of the two logic circuits used for binary addition?

16

What base is used for Hexadecimal numbers? (0x)

16^0, or 1

What is the least significant digit in hexadecimal

1F

0b1110 to Hex = ?

They provide a way of representing binary values using fewer digits, in hex only two hex digits are needed to represent one byte as 1111 = 15

Give one reason why programmers find Hex useful?

A half-adder circuit uses only 2 inputs, A and B, whereas a full adder, is more complicated and uses 3 inputs, A,B and C

What is the difference between a half-adder and a full adder circuit?

A collection of characters, that are used for a specific purpose, such as a language. E.g., in English we use the roman character set

What is meant by the term character set?

128

How many characters could the original 7-bit ASCII code represent?

256

How many characters can be represented by the 8-bit ASCII

Unicode, or the universal character set, allows for non-roman character sets.

What is Unicode?

t allows us to represent a great variety of characters including those from major languages and many other symbols, such as emoji

What does Unicode allow us to do?

Unicode, as it contains significantly more characters.

Which requires more storage space ASCII or Unicode, and why?

Unicode-Transformation-Format, 8 bit. The 8 means that it uses 8-bit blocks to represent a character.

What does UTF-8 stand for, and what is the relevance of the 8

Meaning all encodings in ASCII are the same in UTF-8

The UTF-8 method is backward compatible with ASCII. What does this mean?

UTF-8

What is the main encoding method used on the Internet?

The character set is encoded with codes of different lengths

UTF-8 is a variable-width encoding method, explain this meaning.

The unique binary code that represents each character

What is meant by a code-point in UTF-8

U+0080

Give an example of how a UTF-8 code point is written

They provide standard ways for computers to represent characters that are readable by other computers.

State why ASCII and Unicode are important