math postulates and theorems

addition property

if a=b and c=d, then a+c+b+d

transitive property

if a=b and b=c then a=c

symmetric property of equality

if a = b then b = a

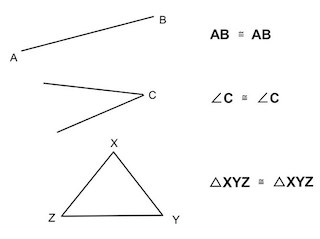
reflexive property

𝐴𝐵≅𝐴𝐵

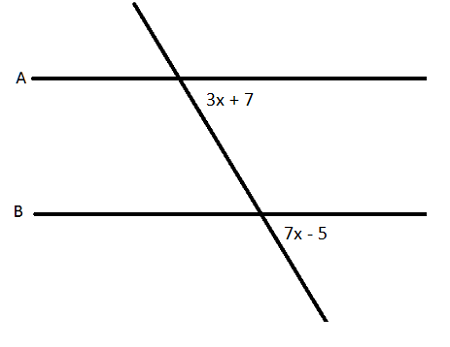
corresponding angles postulate

if two parallel lines are cut by a transversal, then the corresponding angles are congruent

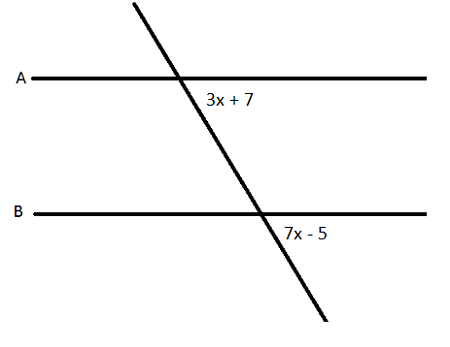
converse of corresponding angles postulate

if two parallel lines are cut by a transversal and corresponding angles are congruent, then the lines are parallel

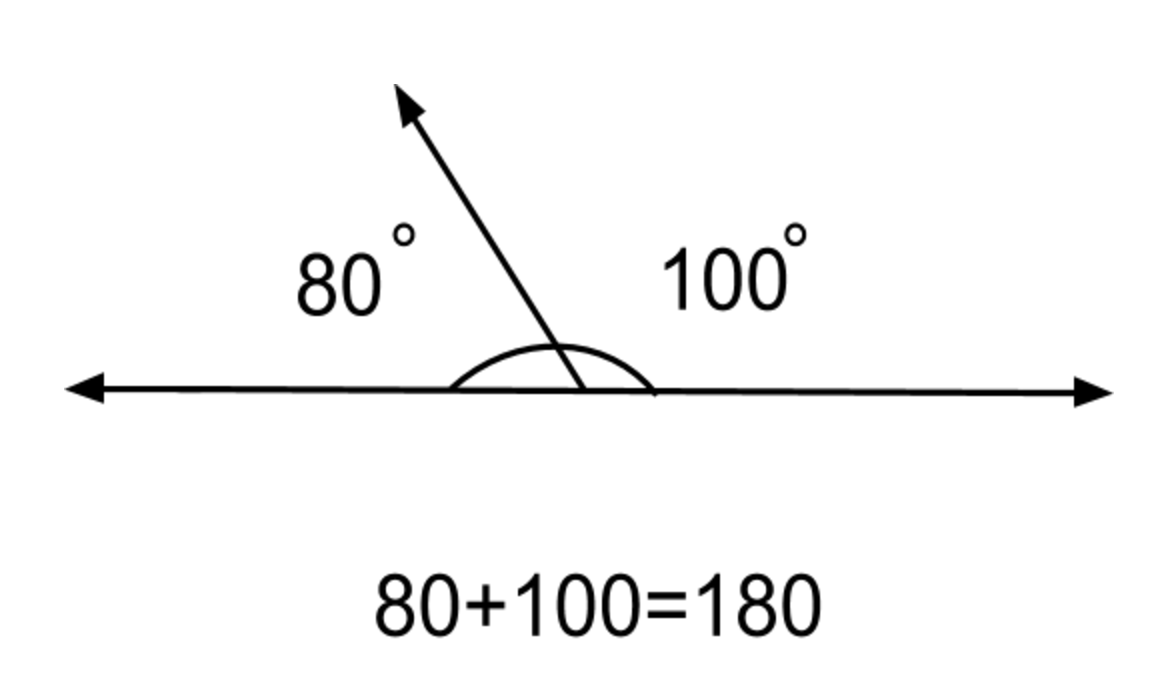
linear pair postulate

two angles that form a linear pair are supplementary, meaning their measures add up to 180

right angle congruence theorem

all 90° / right angles are congruent

congruent supplements theorem

supplements to the same angle or congruent angles and congruent.

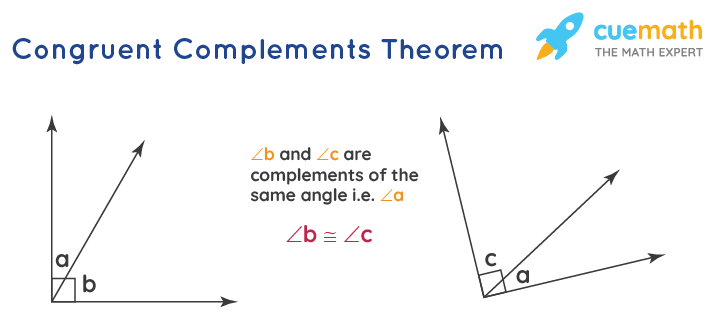
congruent complements theorem

complements to the same angle or congruent angles are congruent.

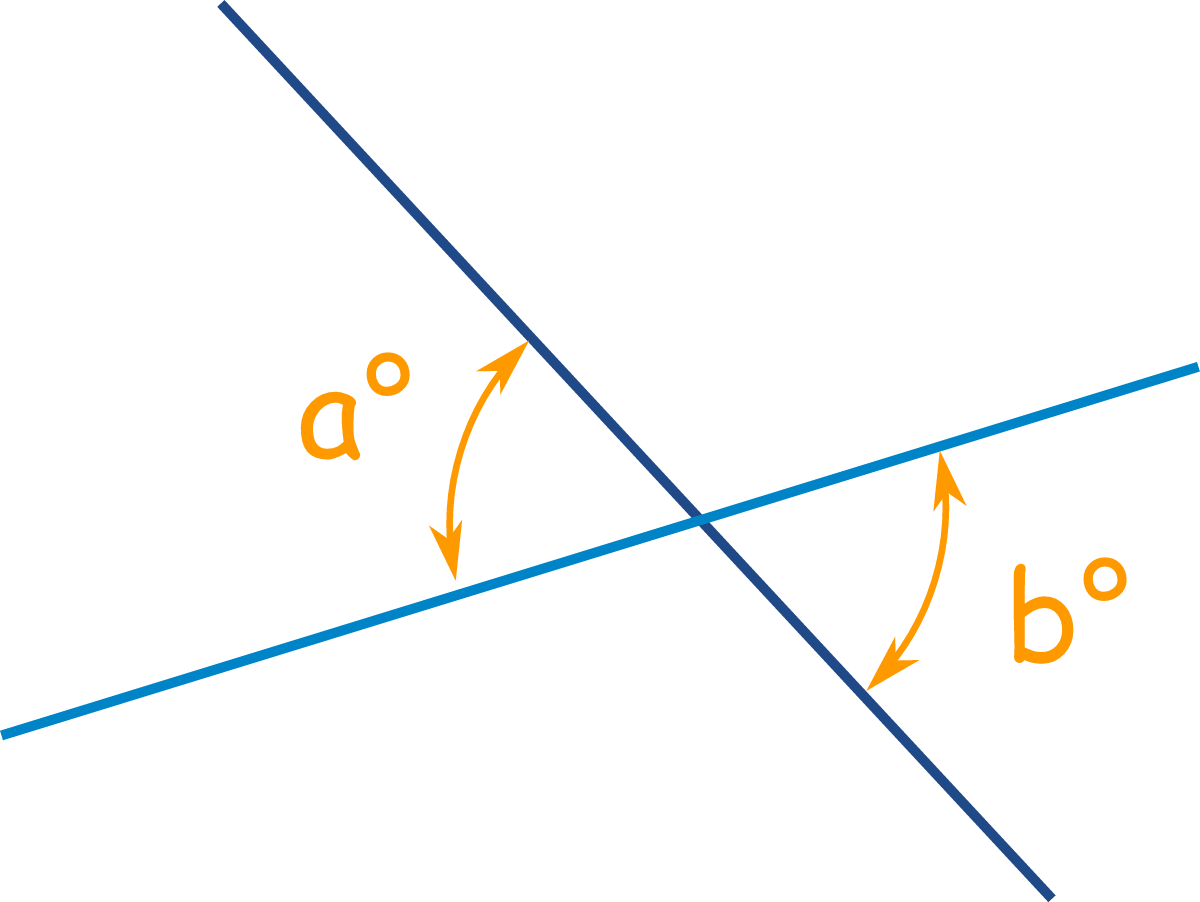
vertical angles congruence theorem

vertical angles are congruent

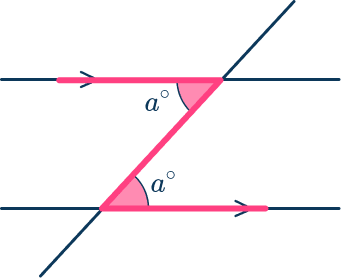
alternate interior angles theorem

if two lines are cut by a transversal, then the pairs of alternate interior angles are congruent

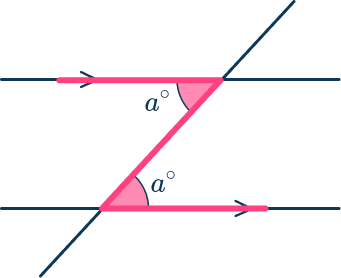
alternate interior angles converse

if two lines are cut by a transversal and alt interior angles are equal then the lines are parallel.

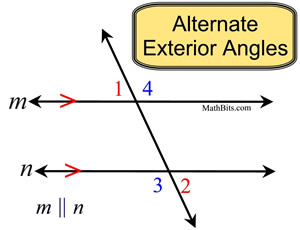
alternate exterior angles theorem

If two parallel lines are cut by a transversal, then the pairs of alternate exterior angles are congruent.

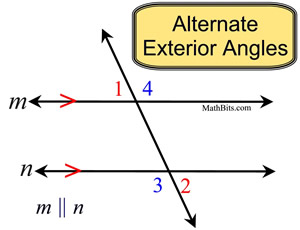
alternate exterior angles converse

if two lines are cut by a transversal and the alternate exterior angles are congruent, then the two lines are parallel

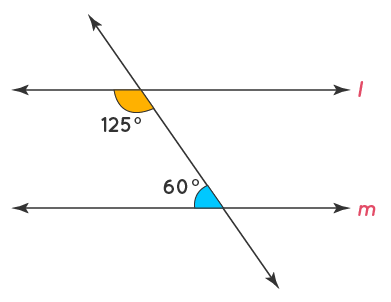
consecutive interior angles theorem

if two parallel lines are cut by a transversal, then the pairs of consecutive interior angles are supplementary.

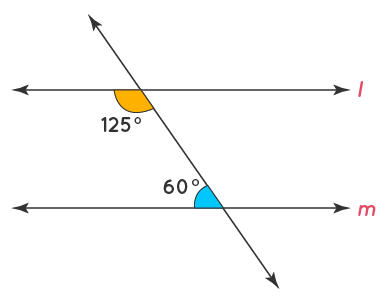
consecutive interior angles converse

If 2 lines are cut by a transversal and same side interior angles are supplementary, then the lines are parallel.

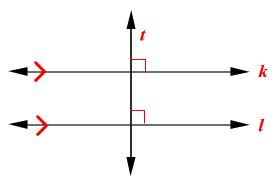
perpendicular transversal theorem

if a transversal is perpendicular to one of the two parallel lines, then it is perpendicular to the other.

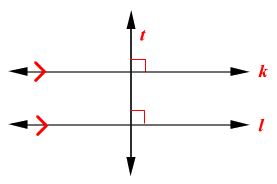
lines perpendicular to a transversal

if two lines are perpendicular to a transversal, then the lines are parallel.

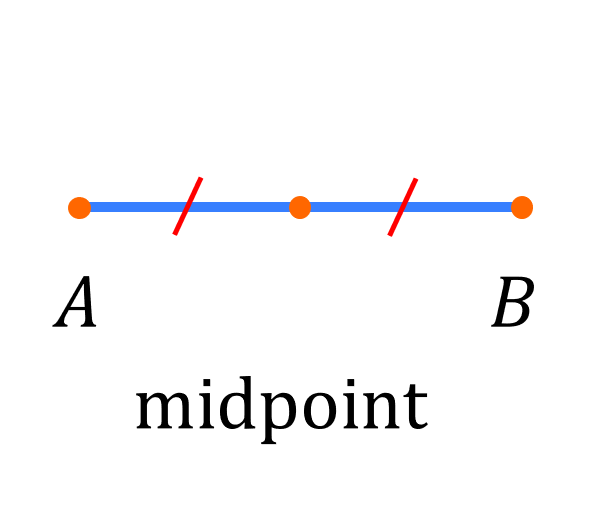
midpoint theorem

if m is the midpoint of AB then AM is congruent to MB.

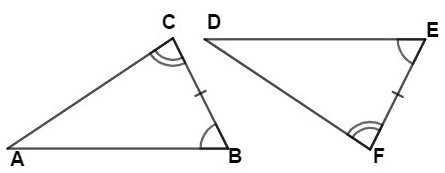
ASA(angle-side-angle) congruence theorem

If two angles and the included side of one triangle are congruent to two angles and an included side of another triangle, then the two triangles are congruent

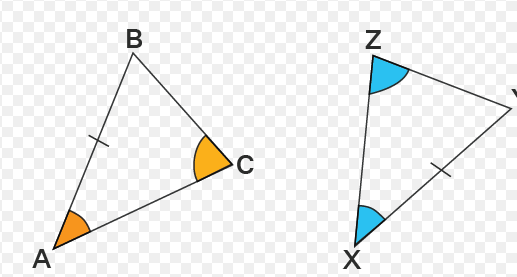
AAS(angle-angle-side) congruence theorem

If two angles and a non-included side of one triangle are congruent to two angles and a non-included side of another triangle, then the two triangles are congruent

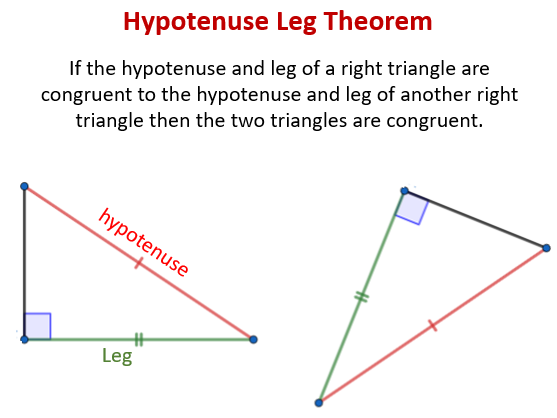
HL (Hypotenuse-lege) congruence theorem

If the hypotenuse and a leg of one right triangle is congruent to the hypotenuse and a leg of another right triangle, then the two triangles are congruent.

AA similarity

two angles in one triangle are congruent to two angles in the second triangle, the triangles are similar

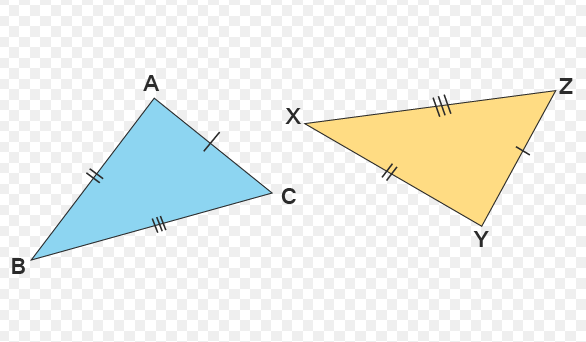
SSS similarity

all 3 sides are in proportion, then the triangles are similar

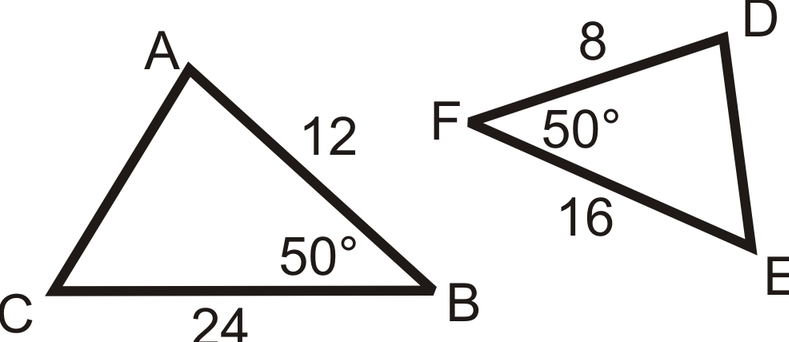
SAS similarity

if two sides are in proportion and the angles are congruent, then the two triangles are similar

distributive property of equality

3(x+y) = 3x + 3y

substitution property of equality

plug it in

division property of equality

divide both sides by the same number

multiplication property of equality

multiply both sides by the same number

subtraction property of equality

subtract the same number from both sides

Angle addition postulate

m∠1 +m∠2 = m∠ABC

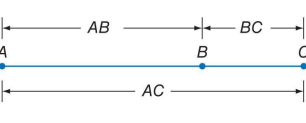
segment addition postulate

AB + BC = AC

law of detachment

If p then q

p is true

q is true

law of syllogism

if p then q & if q then r THEN if p then r