3.3.1.3 Principle of superposition of waves and formation of stationary waves
0.0(0)
0.0(0)
Card Sorting
1/41
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
42 Terms
1
New cards
What is the principle of superposition of waves?
The principle of superposition states when two or more waves with the same frequency arrive at a point, the resultant displacement is the sum of the displacements of each wave.
2
New cards
How are standing waves produced?
Standing waves are produced by the superposition of two waves of the same frequency travelling in opposite directions.
3
New cards
Do stationary waves store or transfer energy?
Stationary waves store energy, unlike progressive waves.
4
New cards
How are standing waves usually achieved?
Standing waves are usually achieved by a travelling wave and its reflection, the superposition produces a wave pattern where the peaks and troughs do not move
5
New cards
What occurs when two waves with the same frequency and amplitude arrive at a point in phase?
They superpose. In phase, constructive interference occurs where the peaks and troughs line up on both waves and the resultant amplitude is double.
6
New cards
What occurs when two waves with the same frequency and amplitude arrive at a point in anti-phase
They superpose. In anti-phase, destructive interference occurs where the peaks on one wave line up with the troughs of the other. The resultant wave has no amplitude.
7
New cards
What does constructive interference look like graphically?
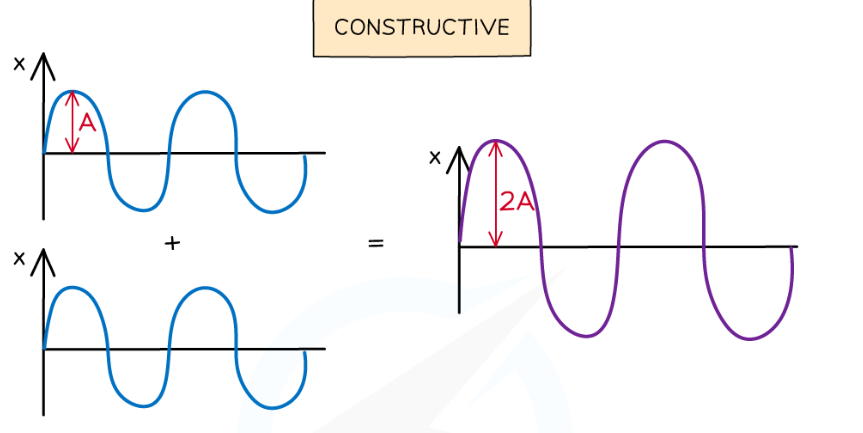
8
New cards
What does destructive interference look like graphically?
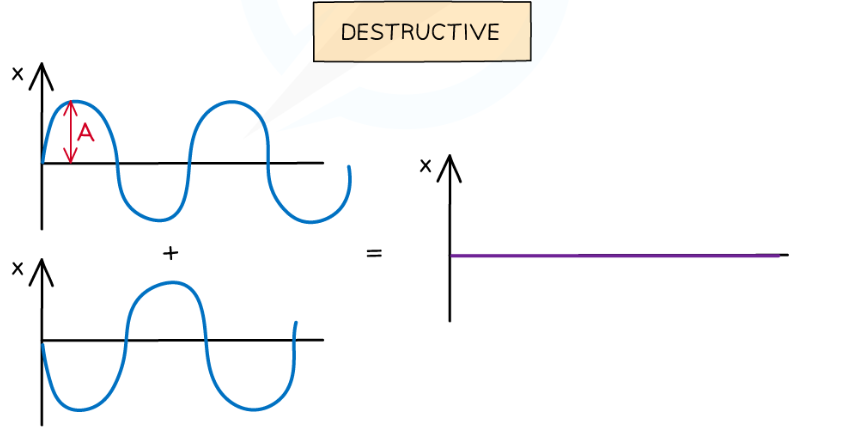
9
New cards
What types of waves do the principle of superposition apply to?
The principle of superposition applies to all types of waves.
10
New cards
When are stationary waves formed?
Stationary waves are formed when two waves travelling in opposite directions along the same line with the same frequency superpose.
11
New cards
What do two waves have to have to form a stationary wave?
They must have the same wavelength, frequency and a similar amplitude.
12
New cards
What type of wave is made up of nodes and anti-nodes?
Stationary waves are made up of nodes and anti-nodes.
13
New cards
What are nodes?
Nodes are regions where there is no vibration on a stationary wave.(A point of minimum or no disturbance)
14
New cards
What are antinodes?
Anti-nodes are regions where the vibrations are at their maximum amplitude on a stationary wave. (A point of maximum amplitude.
15
New cards
Do nodes and antinodes move along a string?
No, nodes are fixed and anti-nodes can only move in the vertical direction.
16
New cards
Are points between nodes in phase with each other?
Points between nodes are in phase with each other
17
New cards
Are points with an odd number of nodes between them in phase?
Points that have an odd number of nodes between them are out of phase.
18
New cards
Are points that have an even number of nodes between them in phase?
Points that have an even number of nodes between them are in phase.
19
New cards
What are nodes and antinodes results of?
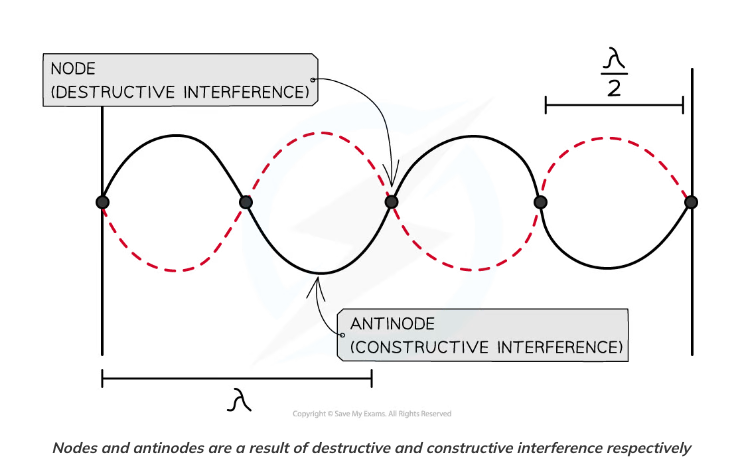
20
New cards
How are nodes spaced apart?
Nodes will always be equally spaced apart based on the wavelength.
21
New cards
Where are antinodes located?
Anti-nodes are located at the midpoint between nodes.
22
New cards
How much energy will particles at the antinodes have?
Particles at antinodes will have the maximum energy available in the wave.
23
New cards
How are stationary waves formed in 4 steps (graphical representation)?
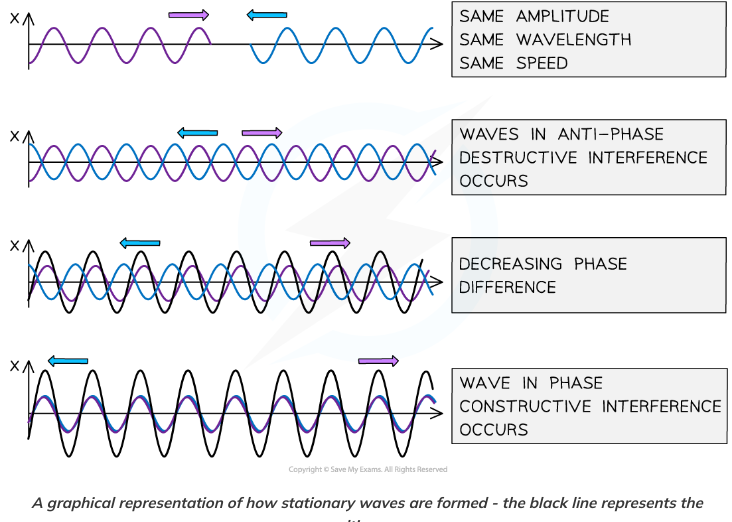
24
New cards
Vibrations caused by stationary waves on a stretched string will produce what?
Vibrations caused by stationary waves on a stretched string produce sound.
25
New cards
How do you produce a stationary wave using microwaves?
A microwave source is placed in line with a reflecting plate and a small detector between the two.The reflector can be moved to and from the source to vary the stationary wave pattern formed.By moving the detector, it can pick up the minima (nodes) and maxima (antinodes) of the stationary wave pattern.
26
New cards
Sound waves can be produced as a result of what?
Sound waves can be produced as a result of the formation of stationary waves inside an air column.
27
New cards
How can the production of sound waves as a result of the formation of stationary waves in an air column be demonstrated?
This can be demonstrated by placing a fine powder inside the air column and a loudspeaker at the open end. At certain frequencies, the powder forms evenly spaced heaps along the tube, showing where there is zero disturbance as a result of the nodes of the stationary wave.
28
New cards
What do the harmonics of stationary waves depend on?
Harmonics depend on the frequency of the vibration and the situation the stationary wave was created in.
29
New cards
When a stationary wave, such as a vibrating string, is fixed at both ends what is the simplest wave pattern it creates?
When a stationary wave, such as a vibrating string, is fixed at both ends, the simplest wave pattern is a single loop made up of two nodes and an antinode (the first harmonic)
30
New cards
What occurs at resonant frequencies?
At specific frequencies, known as resonant frequencies, a whole number of half wavelengths will fit on the length of the string.
31
New cards
What do the resonant frequencies of stationary waves on strings depend on?
The resonant frequencies of stationary waves depend on the length of the string and the wave speed.
32
New cards
For a string with length L, what is the wavelength of the lowest harmonic and why?
For a string of length L, the wavelength of the lowest harmonic is 2L. This is because there is only one loop of the stationary wave, which is a half wavelength.
33
New cards
What is the equation for the frequency of the first harmonic?
f= v/λ= v/2L
34
New cards
How many nodes and antinodes does the second harmonic have?
The second harmonic has three nodes and two antinodes
35
New cards
How many nodes and antinodes does the third harmonic have?
The third harmonic has four nodes and three antinodes
36
New cards
How many nodes and antinodes does the nth harmonic have?
The nth harmonic has n antinodes and n + 1 nodes
37
New cards
What is the wavelength of the second harmonic?
λ=L
38
New cards
What is the frequency of the second harmonic?
f=v/L
39
New cards
What is the wavelength of the third harmonic?
λ=2L/3
40
New cards
What is the frequency of the third harmonic?
f=3v/L
41
New cards
The speed of a wave travelling along a string with two fixed ends is given by what equation?
v= √T/μ
where T=tension (N)
μ= mass per unit length of the string (kg/m)
where T=tension (N)
μ= mass per unit length of the string (kg/m)
42
New cards
What is the equation that leads to the frequency of the first harmonic?
f = (1/2L )(√T/μ)for first harmonic.