Terminology ONLY for Discrete Math Quiz (for memorization only)

make sure to actually study the contents

Discrete Mathematics

• Deals with separate, distinct objects (like whole numbers, graphs, logic statements).

• Common in computer science, since computers work with binary (Os and 1s).

Examples of Discrete Math

integers, algorithms, networks, sets, logic, and graph theory

Continuous Mathematics

• Deals with smooth, unbroken quantities that can take on any value in a range

• Common in engineering, physics, and natural sciences, where change is gradual and measured.

Countable

Values are what In Discrete Mathematics?

Uncountable

Values are what In Continuous Mathematics?

Discrete

countable, step-by-step, digital (like pixels).

Continuous

uncountable, smooth, analog (like a rainbow's gradient).

Proposition

• is a declarative statement that is either TRUE or FALSE, but not both.
  
   statements with a truth value.

NOT A COMMAND

NOT A QUESTION

Logical Connectives

are used to combine or modify propositions to form more complex logical statements.

 rules to combine or change those truth values in propositions

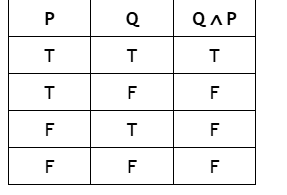
 Conjunction

True only if both propositions are true.
Both must happen.

Example: Miku AND Teto Dance.

AND/BUT

Key Word For Conjunction?

^/HAT

Symbol for Conjunction ?

Disjunction

At least one is true.

Example: “Miku sings OR Teto sings.”
✅ True if Miku sings, Teto sings, or both sing.

OR

Key Word For Disjunction?

v/VEL

Symbol for Disjunction ?

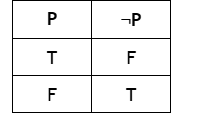
Negation

Reverses the truth value. FLIPPING EVERYTHING

Example: “Miku is on stage.”
➡ NOT = “Miku is not on stage.”

(Just like the equivalent its just changing true to false and Vice Versa)

NOT

Key Word For Negation?

¬ or ~/ TILDE

Symbol for Negation?

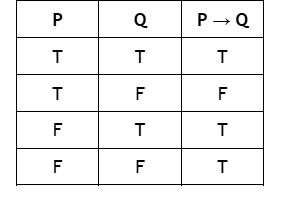
Conditional

The second part depends on the first being true.

Example: “If Miku performs, then Teto will join.”
❌ False only if Miku performs but Teto doesn’t.
✅ In all other cases, it’s true.

IF THEN

Key Word For Conditional?

→/ARROW

Symbol for Conditional?

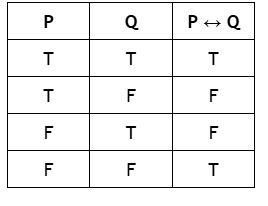
Biconditional

True if both propositions have the same truth value.

They must match.

(either both are true or both are false)

Example: “Miku wears her outfit IF AND ONLY IF Teto wears hers.”
✅ True if they both wear outfits or both don’t.
❌ False if one wears it and the other doesn’t.

Propositions and Connectives

 are the building blocks of logic.
Used in mathematical proofs, programming (if-else statements), and digital circuits.

Truth Tables

is a tool used to show all possible truth values of propositions and how logical connectives affect them.

It lists all combinations of True (T) and False (F) for the given propositions.

Conjunction Truth Table

Negation Truth Table

Disjunction Truth Table

Implication/Conditional Truth Table

Bi Conditional Truth Table

Logical Equivalence

• Refers to two logical statements or propositions that always yield the same truth value (either both true or both false) in every possible scenario. If two statements are logically equivalent, they essentially mean the same thing, even if they are written or structured differently. 

• (Uses ≡ or triple hyphen)

• (Statement A: “If Miku is singing, then Teto is harmonizing.”

• Statement B: “If Teto is not harmonizing, then Miku is not singing.”

These two are logically equivalent — they always match up.
They’re just saying the same thing in different ways:

• Miku singing → Teto harmonizing

• No Teto harmonizing → No Miku singing

Double Negation

states that if you negate a statement twice, you return to the original statement.

Two NOTs cancel each other out.
Like saying: “I don’t dislike Teto.” → which just means “I like Teto.”