Levels of measurement

choosing a statistical test

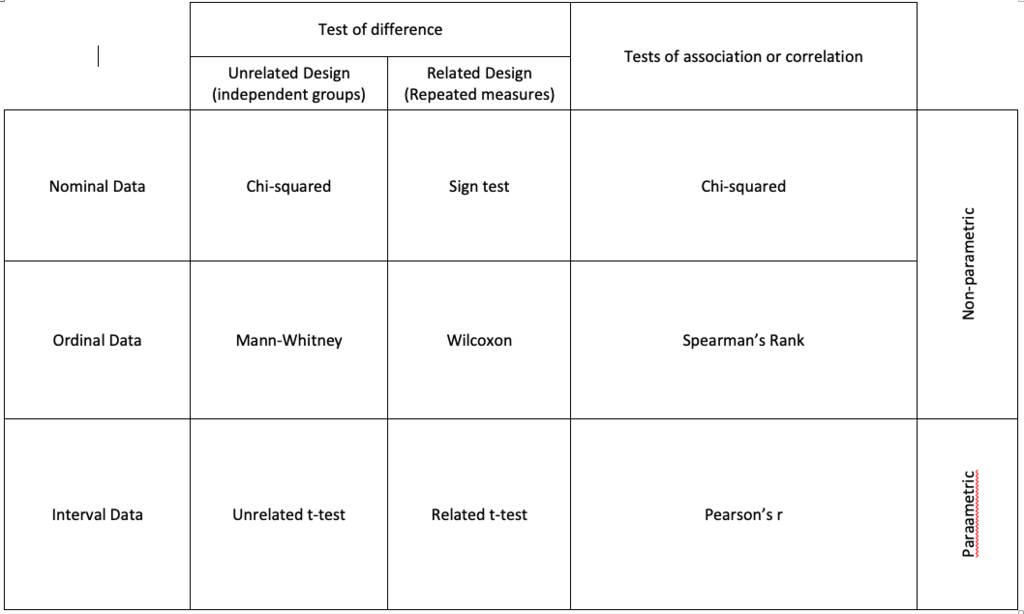
levels of measurement

helps decide which statistical test should be used

nominal, ordinal or interval

nominal data

categorical data

e.g. if a researcher was interested to know if more students doing A-Level Psychology went to a school or college, the data would be categorised as either ‘school’ or ‘college’: two distinct categories

if the data is nominal, then each participant will only appear in one category (discrete data)

ordinal data

ordered or ranked data

e.g. 1st, 2nd, 3rd

is subjective

does not allow for differences in response values to be measured

Likert scales can be used to collect data

usually qualitative

interval data

when there are equal intervals on a measurement scale

e.g. temperature

uses recognised methods of measurement

e.g. seconds, metres, kg

difference between values can be measured

objective and scientific

strength of nominal data

easily generated from closed questions on a questionnaire or interview

limitation of nominal data

has no scale of difference so cannot express the complexity of the data and can be seen as too simple

strength of ordinal data

gives more detail than nominal data as the scores are ordered in a linear fashion e.g. from highest to lowest

limitation of ordinal data

intervals are not of equal value so an average cannot be used

strength of interval data

most informative as the intervals are of equal value so more reliable

limitation of interval data

You can’t say “twice as much” because interval data has no true zero.
Example: 100°C is not twice as hot as 50°C because 0 is not the starting point

ratios are not meaningful