Nuclear and High Energy Particle Physics

file:///C:/Users/yolia/Documents/Uni%20Stuff/Nuclear%20exam%20papers/What_you_need_to_know_from_lectures%20nuclear.pdf

What are isobars?

Nuclei that have the same mass number (total number of protons and neutrons) but different numbers of protons and neutrons.

What are isotones?

Nuclei that have the same number of neutrons but different numbers of protons (different elements).

What are isotopes?

Atoms of the same element that have the same number of protons but different numbers of neutrons.

What is the definition of the mean free path, the equation and define all the symbols

The mean free path is the average distance a particle travels before scattering. It describes the spatial decay of the beam. λ = 1 /nσ where n is the target density and σ is the cross section.

What is the definition of the cross section, the equation and define all the symbols

The cross section represents the probability of a collision between two particles. Rate of collision per unit volume = φnσ where φ is the incident beam flux and n is target density.

Describe how mass spectroscopy works

What are the differences and comparisons that can be made between Rutherford’s and Mott’s cross section models for coulomb scattering?

• Rutherford’s model was developed for non-relativistic alpha particles scattering off small nuclei while Mott’s model includes quantum mechanical properties such as spin

• Rutherford’s model assumes a ‘static’ positively charged nucleus and ignores relativistic effects and spin.

• Mott’s model accounts for deviations observed at higher velocities and scattering angles​.

What is Rutherford’s cross section model suitable for?

It is suitable for low-energy collisions and small scattering angles, where simplifications for relativistic effects and spin are valid​.

What is Mott’s cross section model important for?

It is important for high-energy collisions with high projectile velocities or large scattering angles (θ→180).

What is the definition of nuclear form factor, what does it account for and what is its equation?

The nuclear form factor is a mathematical function that represents the Fourier transform of the nuclear charge distribution, describing how the internal structure of the nucleus modifies the scattering cross section. It accounts for the fact that the nucleus does not behave like a point particle but has a finite size and structure.

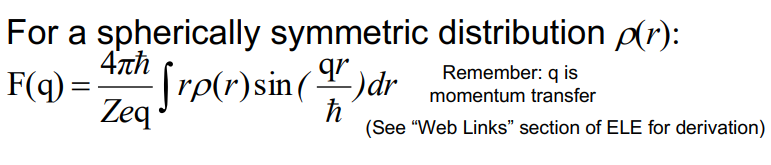
How do diffraction effects in scattering determine charge and mass distributions through Fourier Transformation?

Diffraction patterns arise due to the wave nature of particles interacting with the nucleus. The patterns depend on the nucleus's size and structure. The observed differential cross section is used to calculate the nuclear form factor. The inverse Fourier transform of the nuclear form factor yields the mass distribution of the nucleus.

Therefore, diffraction patterns give info about the internal structure of the nucleus and its charge and mass distributions.

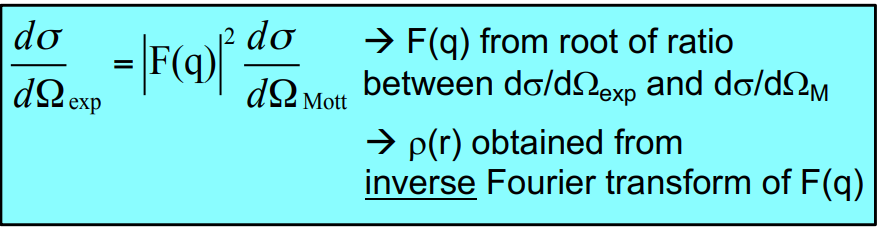
How are the observed differential cross section, Mott cross section and nuclear form factor related? (equation)

check image

What are the limitations of the liquid drop model?

• It doesn’t explain peaks in binding energy or the stability of nuclei with magic numbers (for proton or neutron numbers)

• It doesn’t describe the non-spherical shape of some nuclei

• It doesn’t account for the quantum mechanical properties such as spin, parity, and magnetic moments

• The model relies on experimentally determined constants, making it semi-empirical rather than a fully theoretical description

• It provides limited insights into the spin pairing of protons and neutrons and how this affects nuclear stability

What is the liquid drop model?

It describes the nucleus as a ‘drop’ of incompressible nuclear fluid, with the binding energy of the nucleus calculated as a sum of 5 terms. Each term represents a different physical effect contributing to the stability of the nucleus.

What are the terms in the liquid drop model? (check image for equation, write down terms)

Volume term, surface term, coulomb term, asymmetry term, pairing term

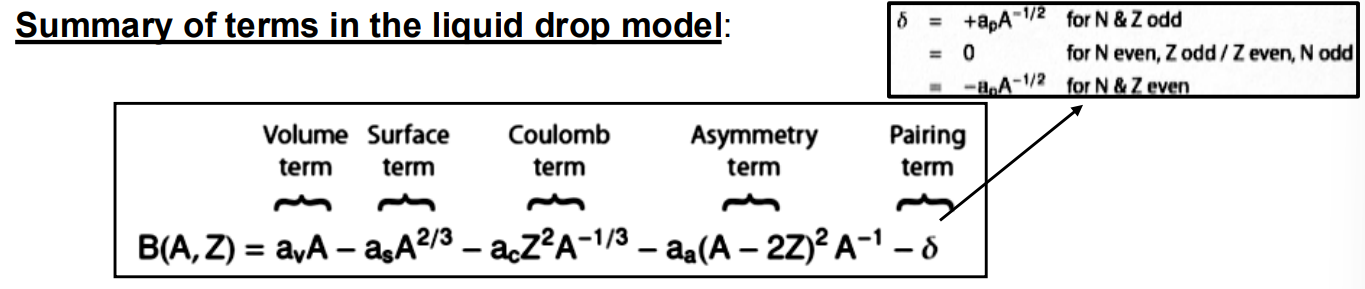
Explain the volume term of the liquid drop model

It represents the binding energy due to the SNF. It is proportional to the total number of nucleons because the centre of the nucleus experiences max binding from surrounding nucleons.

Explain the surface term of the liquid drop model

It accounts for the reduction in binding energy for nucleons on the surface of the nucleus since they have fewer surrounding nucleons. It is proportional to the surface area of the nucleus.

Explain the coulomb term of the liquid drop model

It represents the repulsive electrostatic force between protons inside the nucleus. It is proportional to Z² (number of proton-proton interactions) and inversely proportional to the nuclear radius

Explain the asymmetry term of the liquid drop model

It comes from the Pauli exclusion principle and it minimizes the energy when the number of protons and neutrons are balanced.

Explain the pairing term of the liquid drop model

It represents the extra stability of nuclei with even numbers of protons and neutrons due to spin pairing. It is positive for nuclei with even numbers of protons and neutrons, zero for odd even combos and negative for odd numbers.

What does the liquid drop model assume?

It assumes that the nucleus is spherical and that nucleons behave like molecules in a water drop - short range attractive forces bind with shorter range repulsive forces to prevent collapsing

List the nuclear magic numbers

2, 8, 20, 28, 50, 82 and 126

List the experimental evidence for the existence of magic numbers

• Stability of Isotopes: Isotopes with neutron or proton numbers corresponding to magic numbers are often more stable than those with neighboring numbers

• Nuclear Shell Model: The model predicts that the most stable nuclei are those where nucleons fill energy levels completely, which corresponds to the magic numbers

• Odd-Even Effect: Even-even nuclei (those with both even numbers of protons and neutrons) are generally more stable than odd-odd nuclei. This effect is enhanced for nuclei near magic numbers, where the pairing of nucleons leads to greater stability.

• Neutron Rich Nuclei

• Beta Decay

What is the definition of a nuclear magic number?

They are specific numbers of nucleons in the nucleus of an atom that result in stable configurations.

What are 3 simple solutions to the Schrödinger equation?

Particle in a 1D box (infinite potential well)
Particle in a finite square well
Harmonic oscillator

What is the nuclear shell model?

It describes the arrangement of nucleons in discrete energy levels

What are the 6 principles behind the nuclear shell model?

• Magic numbers correspond to stable nuclei where shells are completely filled

• The Pauli exclusion principle applies

• Energy levels are quantized and grouped into shells, each characterised by quantum numbers

• Nucleons move in a central potential created by the collective interaction of all nucleons

• The Woods-Saxon potential better approximates the nuclear potential than a square well but cannot explain all magic numbers

• Spin-orbit coupling explains all magic numbers by splitting energy levels

What is parity and how is it determined in nuclei?

Parity tells us whether a wavefunction is symmetrical (even) or not (odd). In nuclei, parity is determined by the orbital angular momentum quantum number l (-1)^l

Calculate the spin and parity of O¹⁵₈ oxygen nucleus

Spin = ½ , Parity = -1

What is spin-orbit coupling and explain how it works (4 bullet points)

Spin-orbit coupling arises when a nucleon’s intrinsic spin interacts with its orbital motion, leading to energy level splitting.

• A moving charged nucleon (proton) generates a magnetic field due to its orbital motion

• The nucleon's intrinsic spin interacts with this field, causing a shift in energy levels

• Spin-orbit coupling is strongest at the nuclear surface, where density changes rapidly

• The potential energy of a nucleon due to spin-orbit interaction is proportional to L⋅S (the dot product of orbital and spin angular momenta)

What are the 3 effects of spin-orbit coupling on the nuclear shell model?

• Without spin-orbit coupling, the shell model failed to predict some magic numbers

• Radial-dependent spin-orbit potential causes energy levels to split which correctly explains all magic numbers

• Higher l values experience greater splitting, shifting energy levels significantly​

How to add angular momentum vectors quantum mechanically?

For integer values, (j₁ + j₂) … (j₁ - j₂)

For half integer values, (j₁ + j₂) or (j₁ - j₂)

For multiple integer values, (j₁ + j₂) … (j₁ - j₂) and ((j₁ + j₂) + j₃) … ((j₁ - j₂) - j₃)

Derive and apply the radioactive decay law

check image

What is half-life and its equation?

The time taken for half of the radioactive nuclei to decay T_1/2 ​= ln(2)/λ​

If the Q factor is positive, what happens?

Spontaneous decay

Explain alpha emission probability in terms of barrier tunnelling and the Gamow factor (G)

• Alpha decay occurs via quantum tunnelling through the Coulomb barrier, which classically prevents escape.

• Tunneling probability: T= e^−G, G = 2πZe²/ℏv

• Decay rate: λ = fe^−G, f ≈ v/2R

• Key factors:

  • Lower Z → Weaker Coulomb barrier → Higher decay probability.

  • Higher Q → Faster alpha particle → Increased tunneling.

• Explains why elements with high Q decay faster.

What are the limitations in the Gamow model?

• Shape of potential assumed too simple: Real Woods-Saxon potentials have softer transition to Coulomb dependence

• The model ignores orbital angular momentum effects, which modify the barrier height and tunneling probability.

• The model assumes spherical symmetry only, making it unreliable for non-spherical nuclei.

• The model assumes that alpha particles pre-exist inside the nucleus, ready to escape. However, the probability of alpha cluster formation actually varies between nuclei

What is decay probability?

The chance that an unstable nucleus will undergo radioactive decay within a certain time period

What is mean lifetime and its equation?

The average time a nucleus survives before decaying τ = 1/λ

What is the Q factor?

The change in total binding energy

What are the 3 equations for decay probability?

For a large sample → P_decay = λdt

For a single nucleus → P_survival(t) = e^-λt P_decay(t) = λe^-λt

Describe the "solar neutrino problem"

The Standard Solar Model (SSM) predicts a high flux of electron neutrinos from the Sun's fusion reactions. However, experiments like Homestake detected only about 1/3 of expected electron neutrinos.

Homestake detector and Gallium experiments are sensitive to lower energies and also recorded deficits.

The mismatch between predicted and observed flux is known as the "solar neutrino problem."

What is an idea that can solve the solar neutrino problem?

Electron neutrinos may change flavour (oscillate into muon or tau neutrinos) on their way from the Sun to Earth. Detectors sensitive only to electron neutrinos miss the oscillated neutrinos which explains the lower observed flux.

List the evidence for the existence of neutrinos from the properties of beta decay

• Beta decay electrons/positrons show a continuous range of energies

• "Missing" energy, along with differences in momentum and angular momentum, hinted at a massless, neutral particle.

• To maintain conservation laws, Pauli proposed the neutrino

Describe the basics of operation and results from the Reines and Cowan experiment

A nuclear reactor provides an intense flux of antineutrinos from neutron decay.

• Detection Method:

  • Proton-rich water doped with CdCl​ was used

  • Antineutrino + proton → positron + neutron

  • Positron annihilates with an electron → emits 2 gamma rays

  • Neutron captured by Cd → emits 2 more gamma rays

• Detection Technique:

  • Photomultiplier tubes & liquid scintillators detect gamma-ray pairs

  • Coincidence detection minimizes background noise.

• Outcome: First observation of neutrino interactions, confirmed Fermi’s beta decay theory.

Describe Čerenkov detectors (Super-Kamiokande) and how they work

• A charged particle moving faster than light in water emits Čerenkov radiation—a faint, cone-shaped blue light.

• Super-Kamiokande:

  • Located deep underground to block cosmic rays.

  • Ultrapure water as the detection medium.

  • Photomultiplier tubes capture Čerenkov light.

  • Neutrinos scatter electrons, producing light patterns that reveal energy and direction of the neutrino.

Give quantum mechanical and relativistic interpretations of neutrino oscillations

• Quantum Mechanical Interpretation:

  • Neutrino flavor eigenstates are superpositions of mass eigenstates

  • As they travel, their mass states change phases, leading to flavour oscillations

  • The probability of detecting a specific flavour depends on mass differences (Δm²), energy, and distance traveled

  • Relativistic Interpretation:

  • Neutrinos move almost at the speed of light. Tiny mass differences cause small energy shifts: (E ≈ p + m²/2p).

  • Due to phase shifts, their oscillations extend over vast distances

  • Since they change flavor, they must have mass and can't travel exactly at c

Using the liquid drop model, explain the origin of the barrier to spontaneous fission

According to the liquid drop model, the barrier to spontaneous fission arises from the competition between surface energy and Coulomb repulsion during nuclear deformation:

1. A spherical nucleus minimizes the surface area, which represents the lowest surface energy configuration.

2. As the nucleus begins to deform into a prolate (elongated) shape while maintaining the same volume, the surface area increases, causing the potential energy to rise and the binding energy to decrease.

3. This creates an energy barrier (the "fission barrier") that must be overcome for the nucleus to split.

4. Eventually, if deformation continues, the nucleus separates into two fragments, which lowers the Coulomb repulsion between protons and increases the overall binding energy.

5. For spontaneous fission to occur, the nucleus must either receive enough energy to overcome this barrier or quantum tunnel through it (which has extremely low probability for heavy nuclei).

Explain why symmetric fission is rare in terms of magic numbers

Symmetric fission is rare despite being predicted as energetically favorable by the Semi-Empirical Mass Formula (SEMF) because:

1. The shell model, which incorporates quantum mechanical effects not accounted for in the liquid drop model, predicts asymmetric fission.

2. Fission tends to produce fragments with nucleon numbers close to magic numbers (N=50, N=82, Z=50), which represent closed nuclear shells with exceptional stability.

3. In asymmetric fission of heavy nuclei like uranium-235, one fragment typically has a mass number A ≈ 80-85 (near the magic neutron number N=50) and the other has A ≈ 130-140 (near the doubly magic numbers N=82, Z=50).

4. These magic number configurations provide extra binding energy that makes asymmetric fission energetically favorable despite predictions from the simpler liquid drop model.

5. The quantum shell effects essentially modify the potential energy landscape of the fissioning system, creating valleys that guide the nucleus toward asymmetric division

Explain the difference between fissionable and fissile material

The distinction between fissionable and fissile materials lies in their neutron absorption properties:

Fissionable Materials:

1. Can undergo nuclear fission only when hit by highly energetic neutrons

2. Have a higher activation energy for fission (e.g., uranium-238 requires ~6.5 MeV)

3. Require "fast" neutrons with kinetic energy >1.7 MeV (~0.058c)

4. Have low neutron capture cross-sections

5. Example: uranium-238

Fissile Materials:

1. Can undergo fission with neutrons of any energy, including slow "thermal" neutrons

2. Have lower activation energy for fission (e.g., uranium-235 requires ~5 MeV)

3. Can sustain chain reactions more readily

4. Often have odd numbers of neutrons (which contributes to lower activation energy due to neutron pairing effects)

5. Have much higher neutron capture cross-sections, especially for slow neutrons

6. Examples: uranium-235, plutonium-239, uranium-233

What are chain reactions, and what is the difference between sub-critical and super-critical chains?

Nuclear chain reactions occur when neutrons released from fission events trigger additional fissions in nearby nuclei:

1. In a chain reaction, each fission event releases neutrons that can potentially cause more fission events.

2. The criticality parameter k = nq determines the reaction behavior, where:

   • n = average number of neutrons generated per fission

   • q = probability that a neutron generates further fission

3. Sub-critical chain (k < 1):

   • Each generation produces fewer neutrons than the previous one

   • The reaction gradually dies out

   • Total energy release is finite

   • Safe for controlled environments

4. Critical chain (k = 1):

   • Each generation produces exactly the same number of neutrons

   • The reaction is self-sustaining at a steady rate

   • Used in nuclear power reactors

5. Super-critical chain (k > 1):

   • Each generation produces more neutrons than the previous one

   • The reaction rate grows exponentially

   • Can lead to rapid energy release

   • Used in nuclear weapons

Derive and apply the reaction rate law for nuclear chain reactions

The reaction rate law for nuclear chain reactions can be derived as follows:

1. Consider a neutron that causes a fission event, with:

   • q = probability of generating further fission

   • tg = average time for a fission event to occur

   • n = total neutrons generated in a fission event

   • k = nq = neutrons that go on to cause further fission

2. Starting with one neutron (N₀ = 1), after time δt, the number of neutrons will change by:

   • δN(t) = (k - 1) × N(t) × δt/tg

3. This can be written as a differential equation:

   • dN(t)/dt = (k - 1) × N(t)/tg

4. Integrating this equation:

   • N(t) = N₀ × exp[(k-1)t/tg]

5. For generation number x = t/tg:

   • N(x) = N₀ × exp[(k-1)x]

   • If k > 1, this becomes approximately N(x) = N₀ × exp[(k-1)x] ≈ N₀ × kˣ for large values of k

6. Application: For a chain with k = 3, after 30 generations (x = 30), the number of neutrons is:

   • N(30) = exp(2×30) ≈ 5.71 × 10²⁵

   • Total energy = 200 MeV × 5.71 × 10²⁵ = 0.44 MT (megatons)

What are the basics behind fission reactors, and what is the role of moderators and control rods?

Fission reactors are designed to maintain controlled chain reactions (k ≈ 1) for power generation:

Basic Components:

1. Fuel rods: Contain fissile material (often UO₂ pellets in Zircaloy tubes)

2. Moderator: Material that slows neutrons (H₂O, D₂O, or graphite)

3. Control rods: Neutron-absorbing materials (B₄C, Ag, In, Cd, Hf)

4. Coolant: Removes heat for power generation (water, gas, or liquid metal)

5. Containment structure: Shields radiation and contains pressure

Role of Moderators:

1. Scatter and slow down neutrons from high to thermal energies

2. Increase probability of neutron capture by fuel (higher cross-section)

3. Convert "prompt" neutrons to "delayed" neutrons, allowing better control

4. Extend the time constant (tg) for the chain reaction

5. Common moderators: water (H₂O), heavy water (D₂O), graphite

Role of Control Rods:

1. Absorb excess neutrons to prevent runaway reactions

2. Inserted between fuel rods to reduce k value

3. Precise positioning regulates the neutron population and power output

4. Allow operators to achieve and maintain criticality (k = 1)

5. Provide emergency shutdown capability (SCRAM) by rapid insertion

The reactor design carefully balances these components to achieve safe, controllable power generation while maximizing efficiency and minimizing waste.

Describe nuclear fusion and the problems in utilizing it as a power source.

Nuclear Fusion Definition:

• Fusion is the process where light nuclei combine to form heavier nuclei, releasing energy due to the binding energy difference.

• Fusion reactions are exothermic when light nuclei fuse (unlike fission, which works with heavy nuclei).

• The most favorable reaction is deuterium-tritium (D-T) fusion, which releases 17.6 MeV of energy.

Advantages of Fusion Power:

• Abundant fuel (deuterium from seawater, tritium can be bred from lithium)

• Intrinsically safe: no chain reactions involved

• Relatively short-lived radioactive waste

• No production of CO₂ or atmospheric pollutants

Problems and Challenges:

1. Overcoming Coulomb Repulsion:

   • Unlike fission, fusion requires overcoming the electrostatic repulsion between positively charged nuclei

   • Requires extremely high temperatures (~45 million Kelvin for D-T fusion)

   • Particles need to tunnel through the Coulomb barrier

2. Plasma Confinement:

   • Materials at fusion temperatures exist as plasma and must be confined

   • Magnetic confinement uses powerful electromagnets in a torus/tokamak configuration

   • Maintaining stable plasma confinement is extremely challenging

3. Energy Balance:

   • Energy losses through Bremsstrahlung radiation and imperfect confinement

   • Need to reach "breakeven" where fusion energy output equals input energy

   • Practical reactors need a gain factor >5 (fusion output at least 5× greater than input)

   • JET achieved a record gain of ~2 as of 2022, still below what's needed

4. Engineering Challenges:

   • Requires extremely high-precision feedback control systems

   • Materials that can withstand plasma contact and neutron bombardment

   • Superconducting magnets for sustained operation

   • Complex heating systems (neutral beam injection, ohmic heating, radio frequency heating)

What is Lawson's criterion, and how to use it to describe conditions for a feasible, self-sustaining fusion reaction?

Lawson's Criterion:

• Describes the energy balance required for a self-sustaining fusion plasma

• States that for a plasma to be self-sustaining, the energy released by fusion reactions must equal or exceed the energy lost from the plasma

Mathematical Expression:

• For a deuterium-tritium plasma, the energy balance gives us: $\frac{1}{4}n^2\langle\sigma v\rangle Q = \frac{3nkT}{\tau}$ Where:

  • $n$ is the plasma density (particles per unit volume)

  • $\tau$ is the energy confinement time

  • $T$ is the plasma temperature

  • $\langle\sigma v\rangle$ is the reaction rate parameter

  • $Q$ is the energy released per fusion reaction (17.6 MeV for D-T)

The Triple Product:

• Since $\langle\sigma v\rangle$ and $\tau$ both depend strongly on temperature, it's more useful to express Lawson's criterion as the "triple product": $n\tau T$

• For deuterium-tritium fusion, a self-sustaining reaction requires: $n\tau T > 10^{21}$ keV·s·m⁻³ (or $10^{28}$ K·s·m⁻³)

How to Use It:

• The triple product provides a clear target for fusion reactor design

• Engineers can trade off between:

  • Plasma density ($n$)

  • Confinement time ($\tau$)

  • Temperature ($T$)

• For practical reactors with achievable confinement times >100 seconds, plasma densities of ~$10^{14}$ cm⁻³ are required (compared to atmospheric density of ~$2.7 \times 10^{19}$ cm⁻³)

• Different fusion approaches optimize different aspects:

  • Tokamaks like ITER focus on longer confinement times with moderate density

  • Inertial confinement (laser) approaches like NIF use extremely high densities with very short confinement times

Note: Lawson's criterion concerns the energy balance within the plasma itself, while the fusion gain factor (Q) relates to the total energy transferred to the plasma from external sources.

Explain the very basics of quantum field theory (QFT) and the principles behind exchange particles

• QFT unifies particles and fields: Particles are quantized excitations (ripples) in underlying fields.

• Forces arise from exchange particles (virtual particles):

  • Example: Electromagnetic force is mediated by virtual photons.

  • Strong, weak, and gravitational forces also have their own mediating particles.

• Exchange particles exist briefly due to the energy-time uncertainty principle (ΔE⋅Δt∼ℏ).

• Virtual particles do not obey standard energy-momentum relations and are fundamental to quantum interactions.

What is a regulator function, and how is it used?

• Regulator functions control infinities in quantum field theory (QFT).

• Used to "smooth out" or suppress divergences in calculations by cutting off contributions from high-energy fluctuations.

• Example: Casimir effect calculations use a function g(ν)g(\nu)g(ν) such that:

  • g(ν)=1 at low frequencies.

  • g(ν)→0 at high frequencies (ν→∞).

• The specific form of the regulator should not affect physical results, but it must be physically meaningful (e.g., incorporating material properties like reflectivity).
  (​)

What is the Lamb shift, and how does it provide evidence for virtual photons?

• Lamb shift: A small energy difference between the 2s and 2p levels in hydrogen, contrary to Schrödinger’s predictions.

• Cause:

  • Virtual photons briefly split into electron-positron pairs, altering the Coulomb potential of the nucleus.

  • These interactions cause a minute shift in energy levels, first measured by Willis Lamb and explained by Hans Bethe.

• Significance:

  • Confirms quantum electrodynamics (QED).

  • Demonstrates the real physical effects of vacuum fluctuations and virtual photons.
    (​)

What is the Casimir effect, and how does it provide evidence for virtual photons?

• Casimir effect: A quantum force between two closely spaced, uncharged conducting plates.

• Cause:

  • Fewer virtual photon modes exist between the plates than outside.

  • This creates a pressure difference, pushing the plates together.

• Experimental confirmation:

  • Measured to within 1% of QED predictions.

  • At 10 nm separation, the force is about 1 atmosphere of pressure.

• Significance:

  • Shows that the vacuum contains a fluctuating “sea” of virtual photons.

  • Provides direct evidence for vacuum energy and quantum field effects.
    (​)

What are the basics of the Lagrangian formulation in quantum field theory?

• Lagrangian (L) describes the dynamics of a system in terms of energy and interactions.

• For a free particle (without interactions):

  L = ℏ^2/c^2 (∂^μ ψ)(∂_μ ψ) − m^2ψ^2

• Interactions require additional terms, e.g., for electron-photon interactions: L_int = e ψˉ γ^μ A_μψ

• Gauge invariance ensures the Lagrangian remains unchanged under local transformations, leading to force-mediating fields.

• Used to derive Feynman rules and equations of motion.
  (​)

What is the equation for the Yukawa potential, and how does exchange particle mass determine interaction range?

• Yukawa potential describes a force mediated by a massive exchange particle:
  V(r) = −g^2 e^(−r/R)/r where:

  • g = coupling strength,

  • R = ℏ/mc = range of interaction,

  • m = mass of the exchange particle.

• Key insight:

  • Lighter exchange particles → longer-range forces (e.g., photons in electromagnetism).

  • Heavier exchange particles → shorter-range forces (e.g., pions in the strong nuclear force).
    (​)

How do pions mediate nucleon-nucleon interactions?

• Direct potential (π⁰ exchange):

  • No charge exchange, affecting proton-proton and neutron-neutron interactions.

  • Weaker than exchange potential (not seen in nature for neutron-neutron).

• Exchange potential (π⁺/π⁻ exchange):

  • Causes proton-neutron conversion (p↔n).

  • Observed in p-n scattering experiments.

• Role of pions:

  • Act as force carriers for the residual strong force (nucleon-nucleon interaction).

  • Unlike photons, pions have mass, limiting the force range to ~1 fm.
    (​)

Why do gluon-gluon interactions determine the short range of the strong interaction?

Unlike photons, gluons carry color charge and can interact with each other. This leads to "colour confinement," where the force between quarks increases as they separate. As a result, quarks cannot be isolated, and the strong force remains short-ranged.

know that gluon-gluon interactions in hadrons ultimately determine the short range of the strong interaction

What are some key deficiencies of the Standard Model?

• Does not explain dark matter or dark energy (~96% of the universe).

• Lacks a quantum treatment of gravity.

• Cannot explain the large matter-antimatter asymmetry (~10^9:1).

What are some basic properties of the Higgs boson?

• Scalar boson (spin=0s) with mass ~125 GeV/c^2

• Carries weak isospin, interacts via the weak force.

• Couples to all massive weak bosons (W+, W-, Z0)

• Interaction strength depends on particle mass

How does the Higgs mechanism lead to mass generation?

• A Higgs field with a "Mexican hat" potential acquires a vacuum expectation value.

• This breaks electroweak symmetry, giving mass to W and Z bosons.

• Fermions gain mass via their interaction with the Higgs field.

What is CP violation in the weak interaction?

CP violation occurs when the weak interaction does not conserve the combined symmetry of charge conjugation (C) and parity (P). This means that the weak force behaves differently for particles and antiparticles.

Give an example of CP violation (check image​)

CP violation was first observed in the decay of the long-lived neutral kaon

Both decay channels occur, but with a small asymmetry, indicating CP is not perfectly conserved.

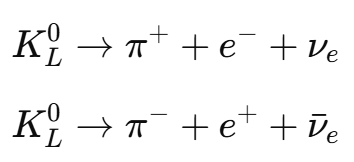
Why is CP violation important in terms of universal particle/antiparticle ratios?

CP violation is crucial for explaining why the universe is dominated by matter over antimatter. The observed matter-antimatter asymmetry suggests that CP violation must have played a role in the early universe, though the Standard Model can only account for a small part of this asymmetry.

What is a Boson? Give some examples

It is a particle with integer spin that mediates fundamental forces. Examples: photon (γ), W and Z bosons, gluons and the Higgs boson.

What is a Fermion?

It is a particle with half-integer spin that follows the Pauli exclusion principle. Example: quarks, leptons

What is a Lepton? Give some examples

It is a fundamental fermion that does not experience the strong interaction. Examples: electron, muon, tau and their associated neutrinos.

What is a Hadron and its two main types?

It is a composite particle made of quarks, bound by the strong force. Two main types: baryons and mesons.

What is a Baryon? Give 2 examples and their quark structure

It is a hadron composed of three quarks. Examples: proton (uud), neutron (udd)

What is a Meson? Give 2 examples

It is a hadron composed of a quark-antiquark pair. Examples: pions and kaons

Draw a Feynman diagram for beta minus and beta plus decay

check image

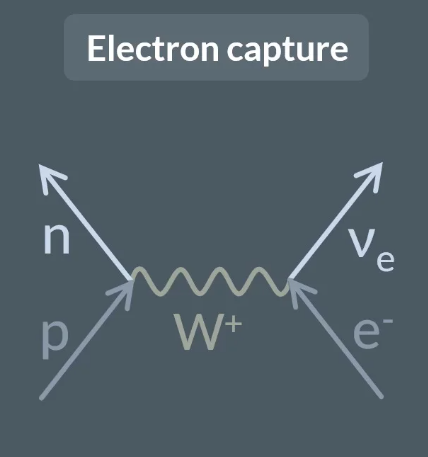
Draw a Feynman diagram for electron capture

check image

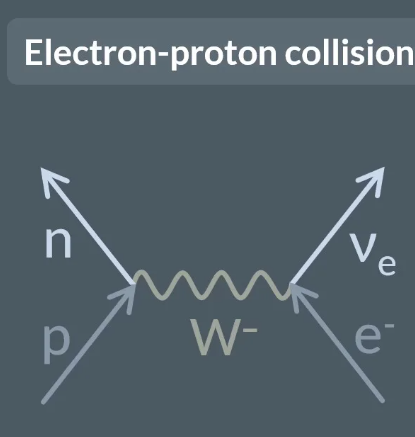
Draw a Feynman diagram for electron-proton collision

check image

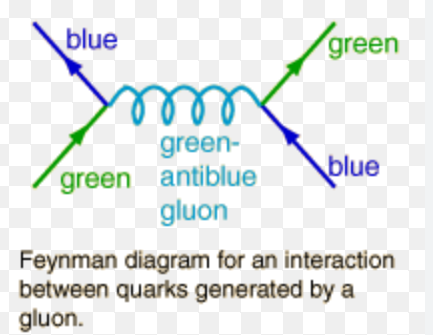
Draw a Feynman diagram for a strong interaction between green and blue colour charged quarks generated by a gluon

check image