trig flashcards pt. 2! 100+ cards

What is Trigonometry?

Trigonometry is a branch of mathematics that studies relationships involving lengths and angles of triangles

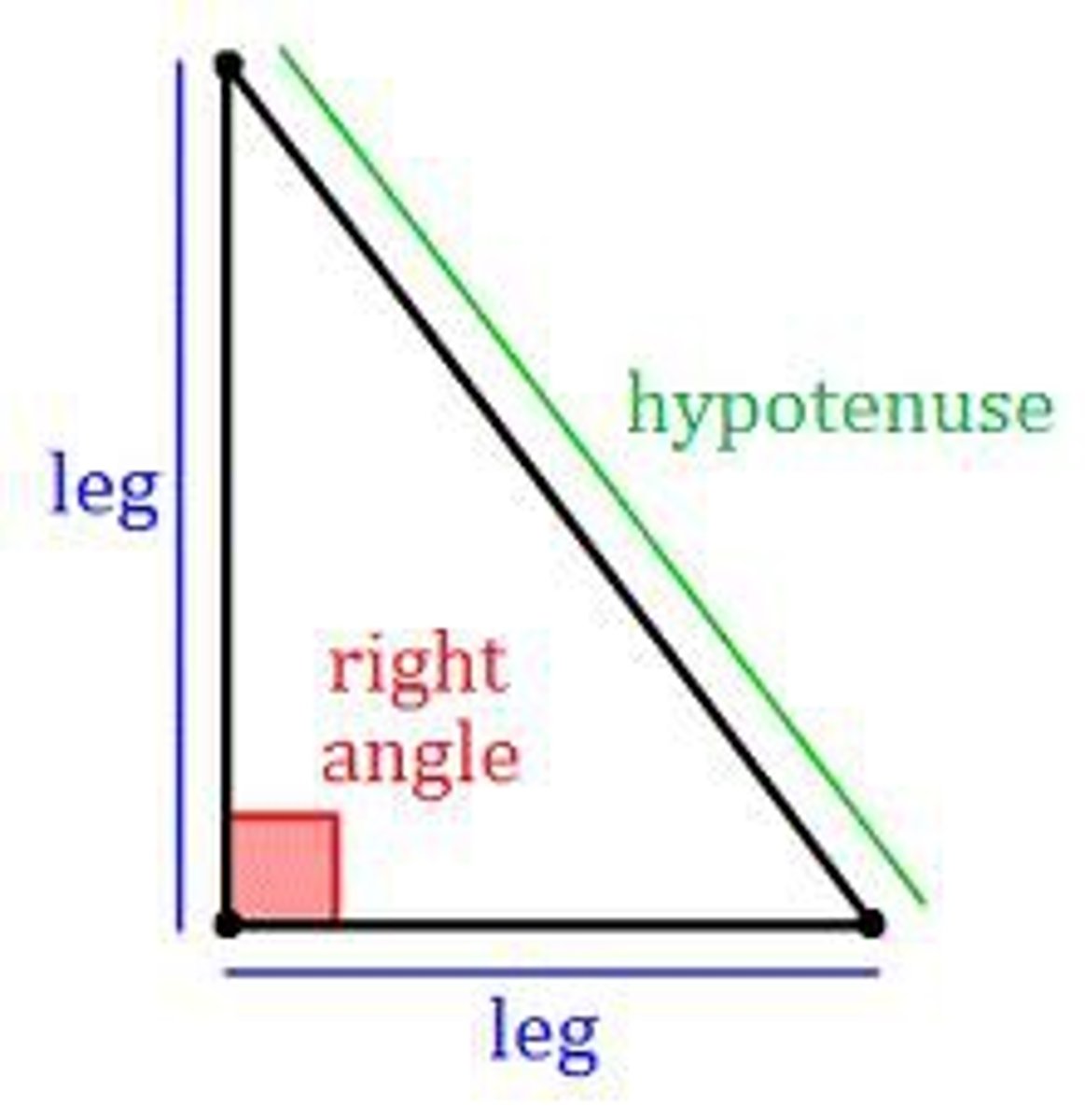
What is the hypotenuse of a triangle?

It's the longest side of a triangle.

The right angle symbol points to it.

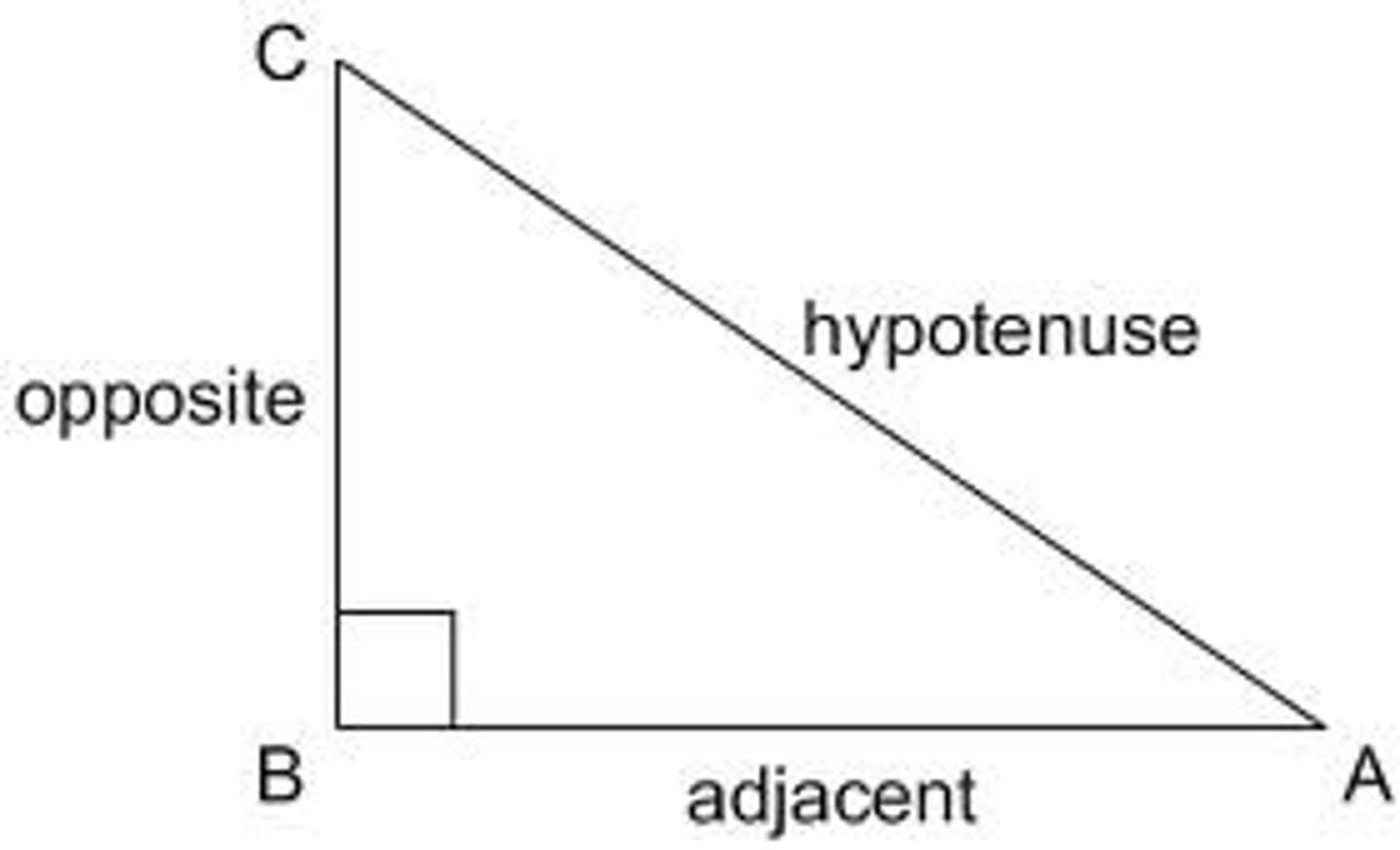
What is the adjacent side of a triangle?

The adjacent is the side adjacent to the angle of reference within the discussion.

The adjacent and opposite side can switch places if the reference angle changes.

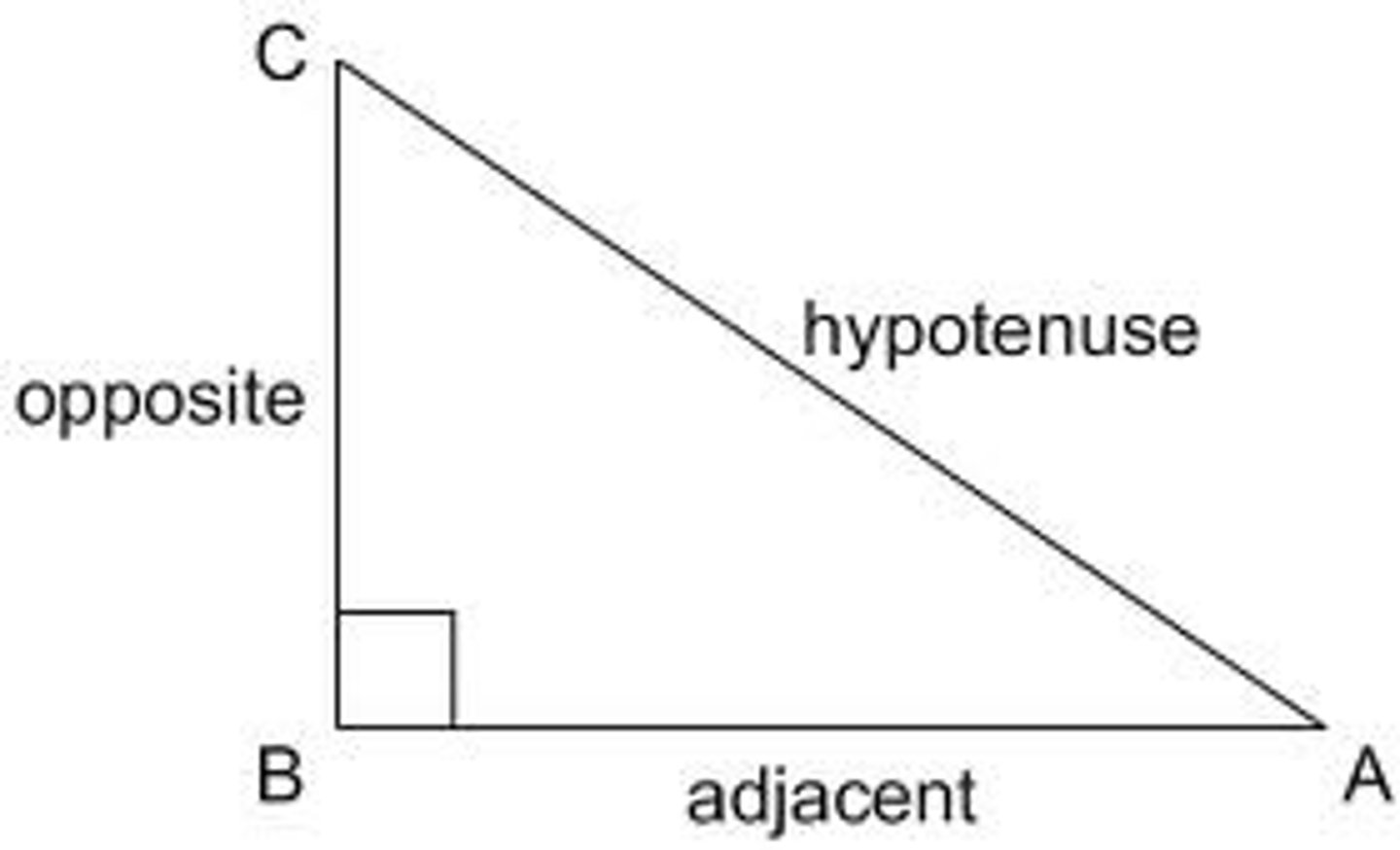
What is the opposite side of a triangle?

The opposite is the side opposite the angle of reference within the discussion.

The adjacent and opposite side can switch places if the reference angle changes.

What's the formula for sin∅?

Sin∅ = opposite/hypotenuse

If in the form (x,y)

Sin∅ = y/r

r=radius

What is the formula for cos∅?

Cos∅ = adjacent/hypotenuse

If in the form (x,y)

cos∅ = y/r

r=radius

What is the formula for tan∅?

tan∅ = opposite/adjacent

If in the form (x,y)

tan∅ = y/x

What is the formula for sec ∅?

Sec ∅ = hyp/adj

or 1/cos

What is the formula for cotan ∅?

Cotan = adj/opp

or 1/tan

What is the formula for cosec ∅?

Cosec ∅ = hyp/opp

or 1/sin

What is the mnemonic for sine, cosine, and tangent?

SOH CAH TOA

sin∅ = opposite/hypotenuse

cos∅ = adjacent/hypotenuse

tan∅ = opposite/adjacent

What are the steps solving for an unknown side of a right angle triangle?

1. Name the sides

2. Find the variable

3. Pick the Trig function

4. Write the equation

If two angles have the sum of 90 degrees, what are they referred as?

Complementary angles and each angle is the complement of the other.

If two angles have the sum of 180 degrees, what are they referred to as?

Supplementary angles

What is a straight angle?

an angle of 180°

What is an acute angle?

The acute angle is the small angle which is less than 90°. If you choose the larger angle you. will have a Reflex Angle instead: The smaller angle is an Acute Angle, but the larger angle is a Reflex Angle

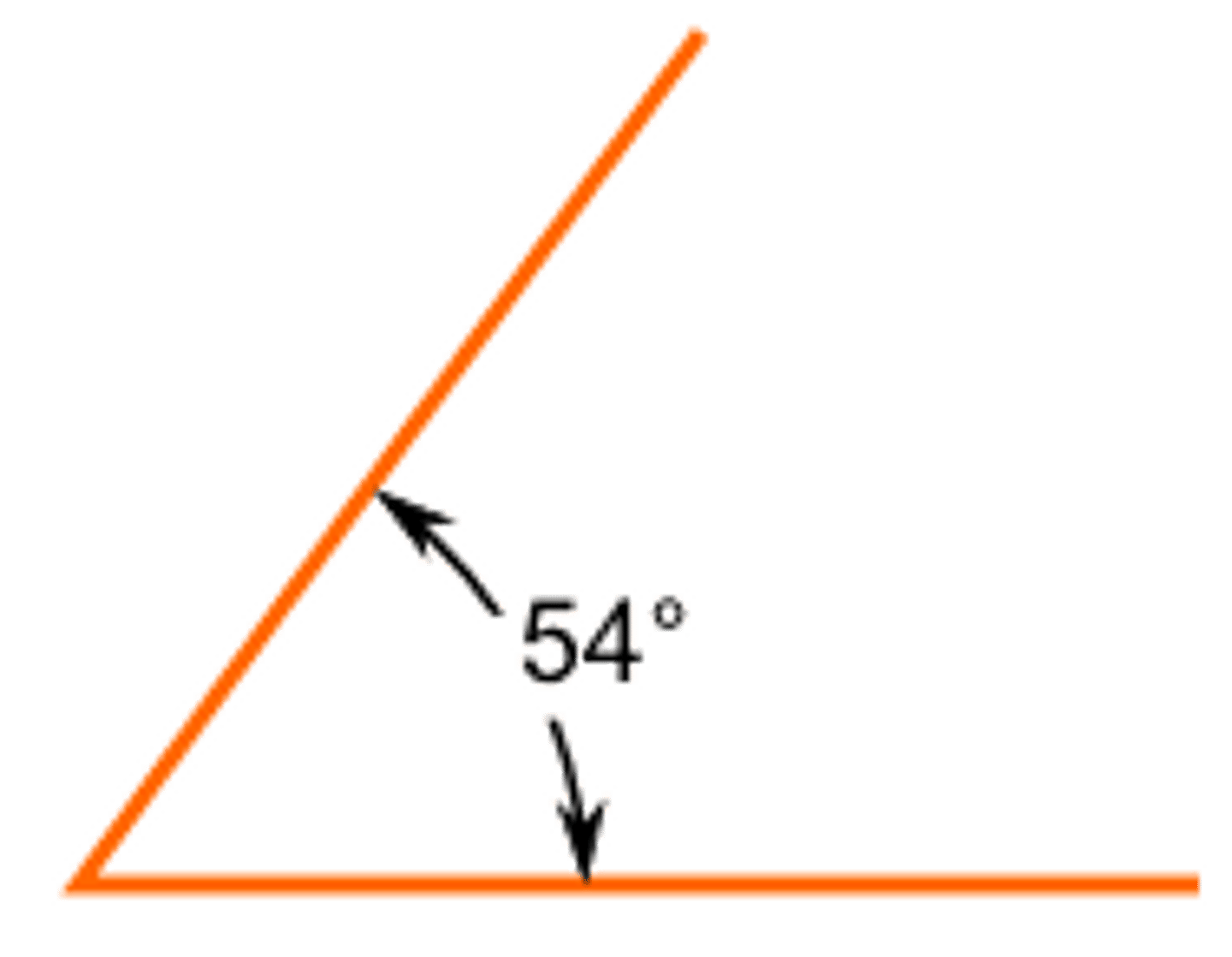
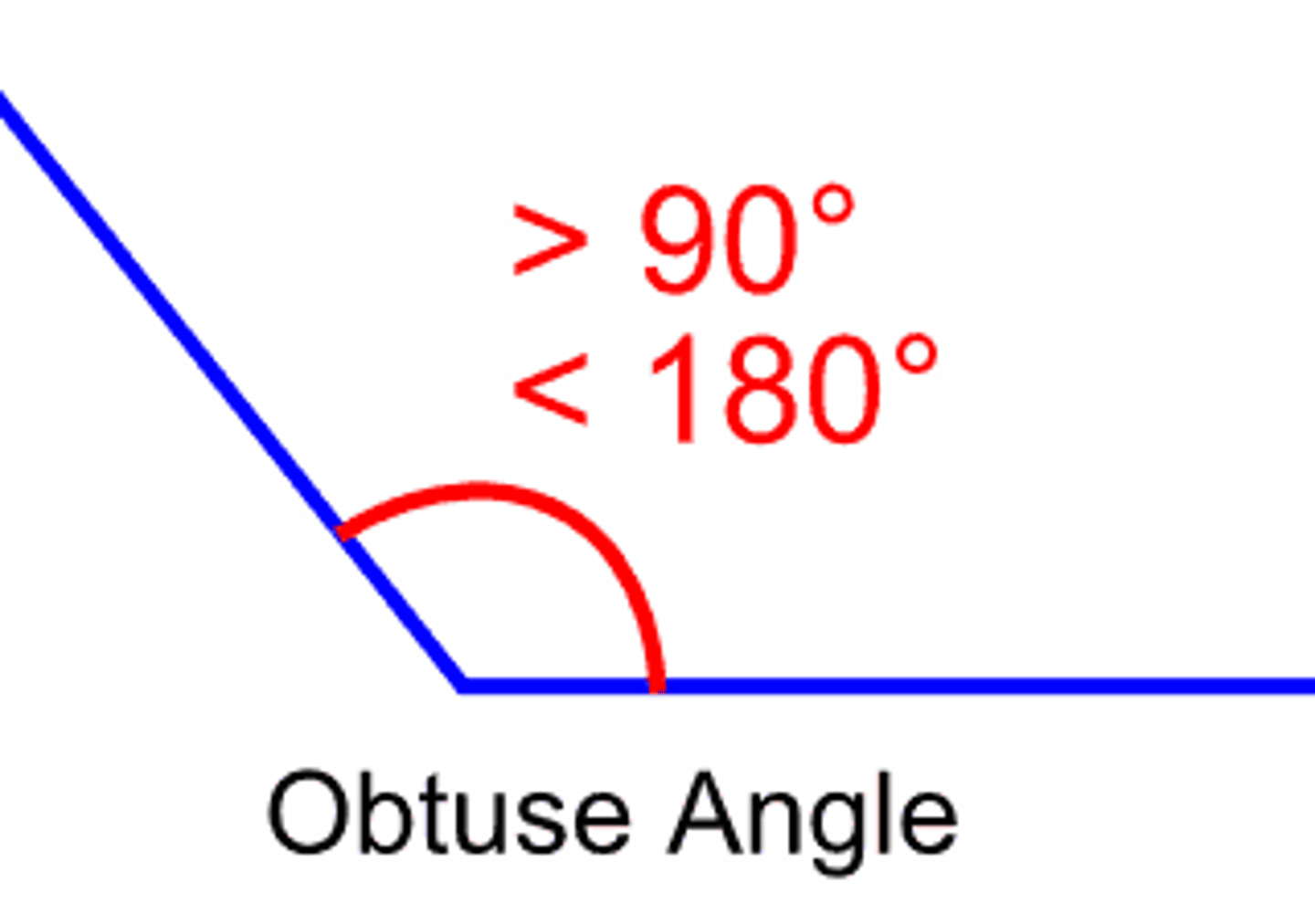
What is an obtuse angle?

The obtuse angle is the smaller angle. It is more than 90° and less than 180°. The smaller angle is an Obtuse Angle, but the larger angle is a Reflex Angle

How does one find the complement to an angle?

How does one find the the supplement to an angle?

Complement 90 - angle

Supplement 180 - angle

What is an isosceles triangle?

An isosceles triangle is a triangle with (at least) two equal sides

What is an scalene triangle?

All the sides and angles are different

What is an obtuse triangle?

An obtuse triangle has exactly one

obtuse angle.

The obtuse angle is the smaller angle. It is more than 90° and less than 180°. The smaller angle is an Obtuse Angle, but the larger angle is a Reflex Angle

What is an acute triangle?

An acute triangle is a triangle with all three angles acute (less than 90°).

What is the sum of all angles in a triangle?

180 degrees

What is the formula for the area of a triangle?

Area = 1/2(base)(height)

In any right triangle in which the two acute angles are 30° and 60°, what are the longest and medium sides?

the longest side (the hypotenuse) is always twice the shortest side (the side opposite the 30° angle), and the side of medium length (the side opposite the 60° angle) is always √3 times the shortest side.

In any right triangle in which the two acute angles are 45° and 45°, what are the longest and medium sides?

If the two acute angles in a right triangle are both 45°, then the two shorter sides (the legs) are equal and the longest side (the hypotenuse) is √2 times as long as the shorter sides. That is, if the shorter sides are of length t, then the longest side has length t√2

What is arc tangent?

a mathematical function that is the inverse of the tangent function

What is the formula to find the distance between two points?

r = √((x₂ - x₁)² + (y₂ - y₁)²)

What is the terminal side of a triangle and which is the initial side?

Terminal side of an angle - trigonometry. In trigonometry an angle is usually drawn in what is called the "standard position." In this position, the vertex of the angle is on the origin, with a fixed side lying at 3 o'clock along the positive x axis.

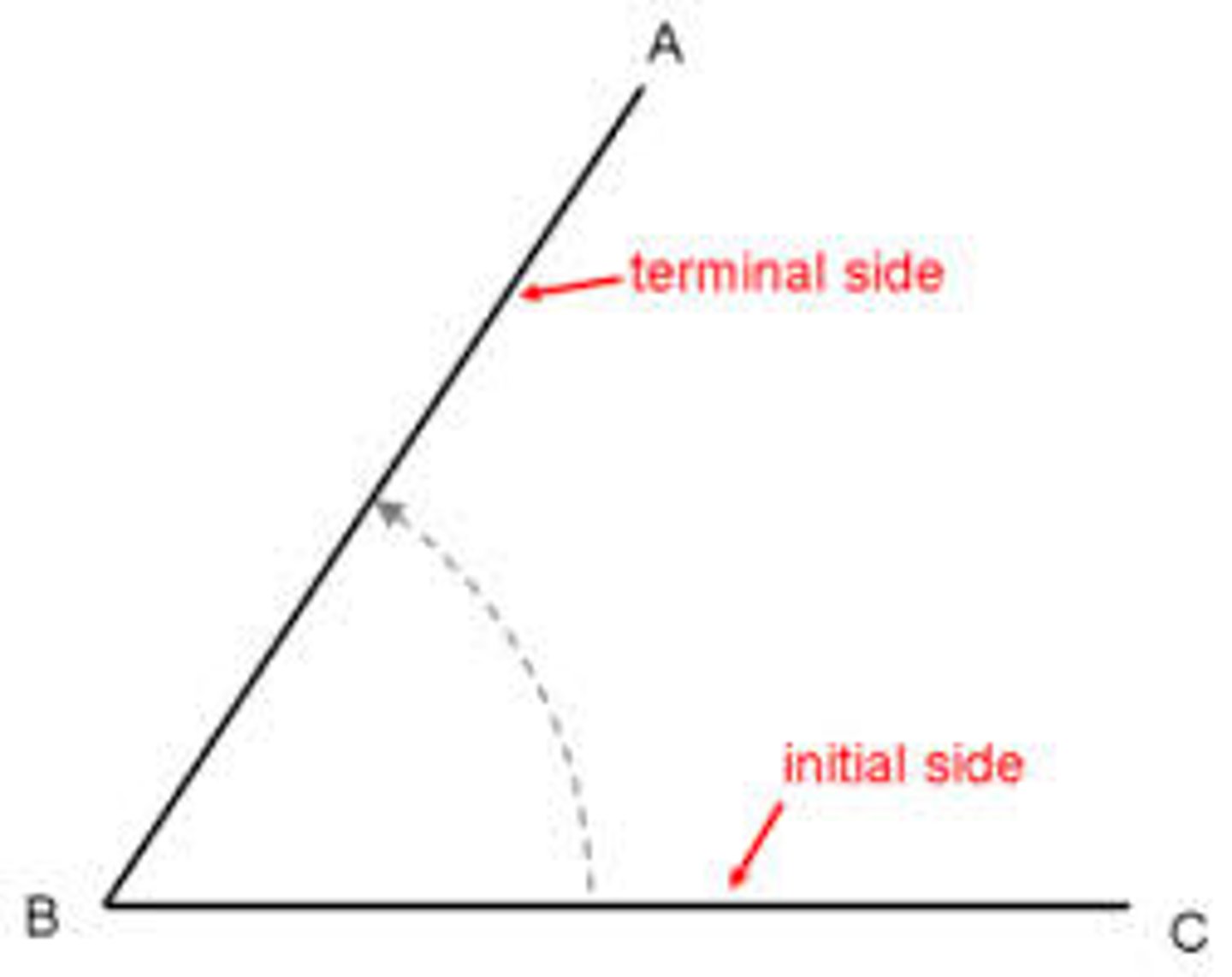
If the terminal side of an angle in standard position lies along one of the axes, the angle is called?

A quadrantal angle

What is STANDARD POSITION for an angle?

An angle is said to be in STANDARD POSITION if its initial side is along the positive x-axis and its vertex is at the origin.

What is the equation for a circle?

The center-radius form of the circle equation is in the format (x - h)² + (y - k)² = r², with the center being at the point (h, k) and the radius being "r".

Side Bar:

If the center is at the origin, then the formula is the same a the Pythagorean Theorem.

How do you find coterminal angles?

Just add or subtract 360⁰

The Cartesian plane is divided into how many regions, and how are they numbered?

There are four regions numbered I-IV, counter-clockwise.

The notation ∅ ∈ QIII means what?

∅ is in standard position and its terminal side lies in quadrant III.

What is the unit circle?

In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, the unit circle is the circle of radius one centered at the origin (0, 0) in the Cartesian coordinate system in the Euclidean plane.

The tan ∅ can be interpreted as what of a line?

Slope of the line

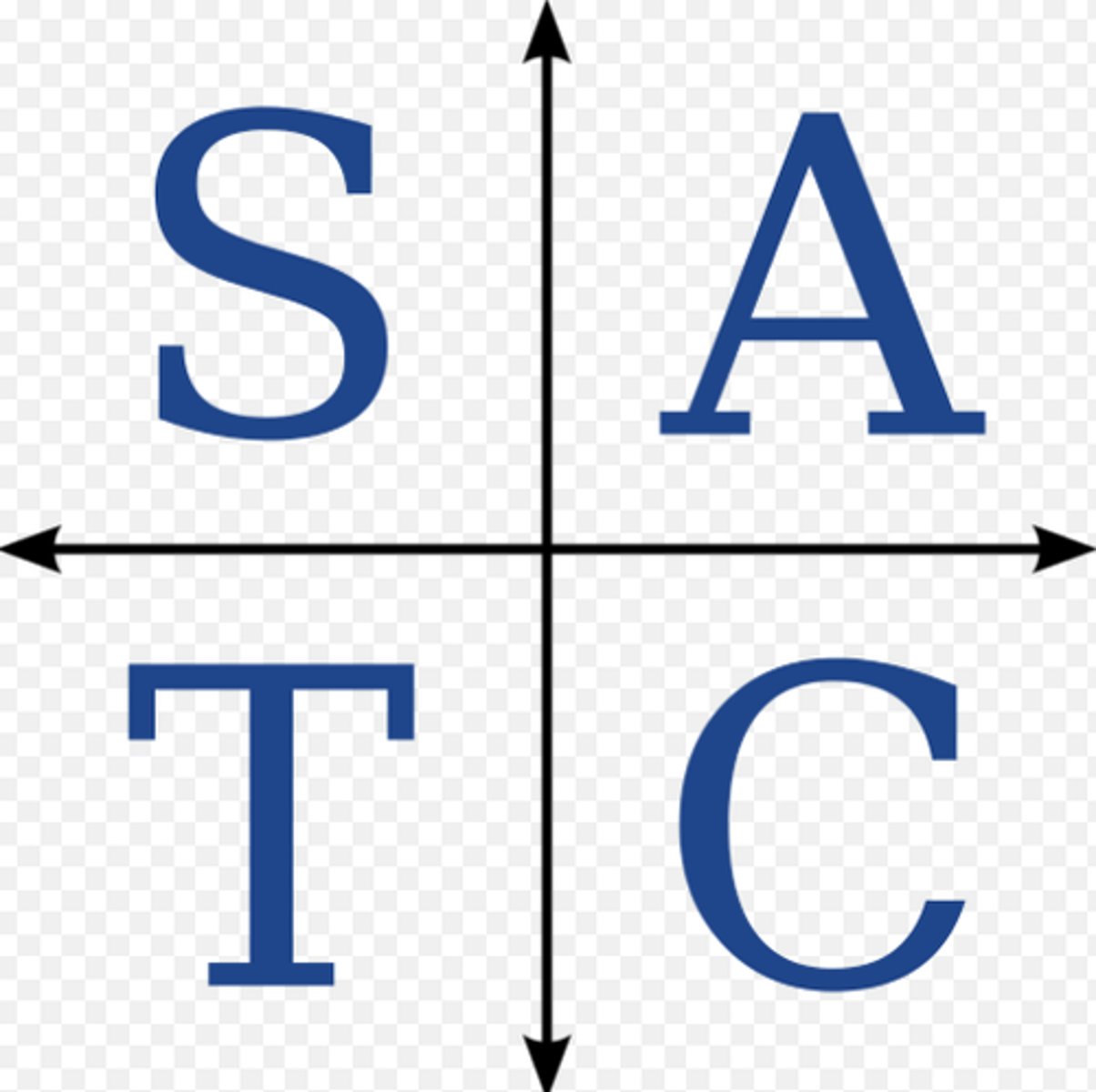
Trig Functions Quadrants

What is the mnemonic?

All

Students....sin, csc

Take..........tan, cotan

Calculas.....cos, sec

The function and it's reciprocal will be the only positive functions.

What is the Cofunction Theorem?

A trig function of an angle is always equal to the cofunction of the complement of the angle.

To clarify this further, if two angles are complementary, such as 40° and 50°, then

a trigonometric function of one is equal to the cofunction of the other. That is,

sin 40° = cos 50°, sec 40° = csc 50°, and tan 40° = cot 50°.

What are the cofunctions for each?

sin

tan

sec

cos

cot

csc

What is the

sin

cos

tan

of 30⁰

sin of 30⁰ is 1/2

cos of 30⁰ = √3/2

tan of 30⁰ = √3/3

What is the

sin

cos

tan

of 45⁰

sin of 45⁰ is √2/2

cos of 45⁰ = √2/2

tan of 45⁰ = 1

What is the

sin

cos

tan

of 60⁰

sin of 60⁰ is √3/2

cos of 60⁰ = 1/2

tan of 60⁰ = √3

What is the

sin

cos

tan

of 0⁰

sin of 0⁰ is √0/2

cos of 0⁰ = √4/2 =1

tan of 0⁰ = 0

What is the

sin

cos

tan

of 90⁰

sin of 90⁰ is √4/2 =1

cos of 90⁰ = √0/2 = 0

tan of 90⁰ = undefined

The number of significant digits (or figures) in a number is found by counting all

the digits from left to right beginning with the first nonzero digit on the left. When

no decimal point is present, trailing zeros are not considered significant.

0.042 has two significant digits

0.005 has one significant digit

20.5 has three significant digits

6.000 has four significant digits

9,200. has four significant digits

700 has one significant digit

What is an Angle of Elevation?

An angle measured from the horizontal up.

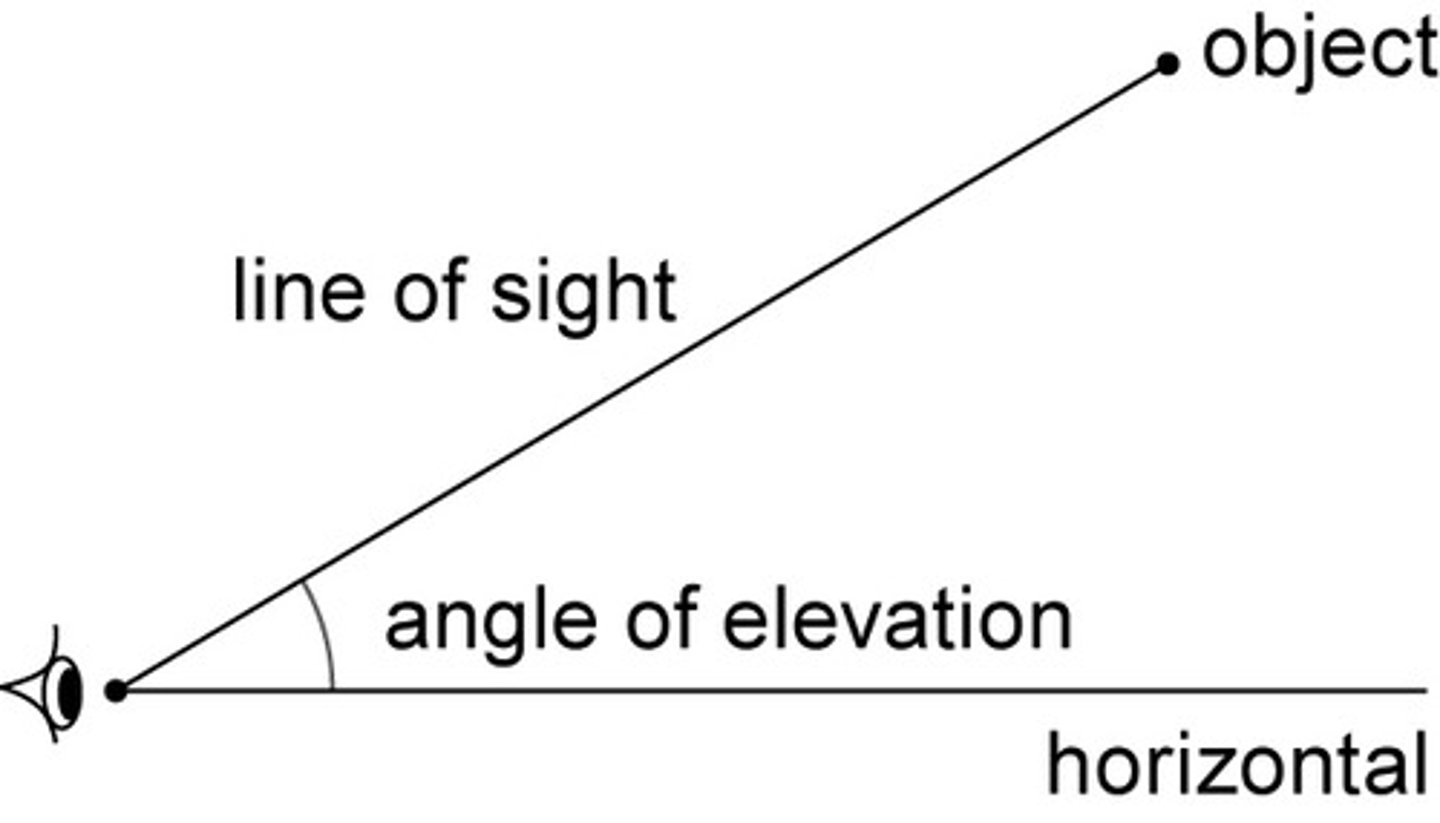
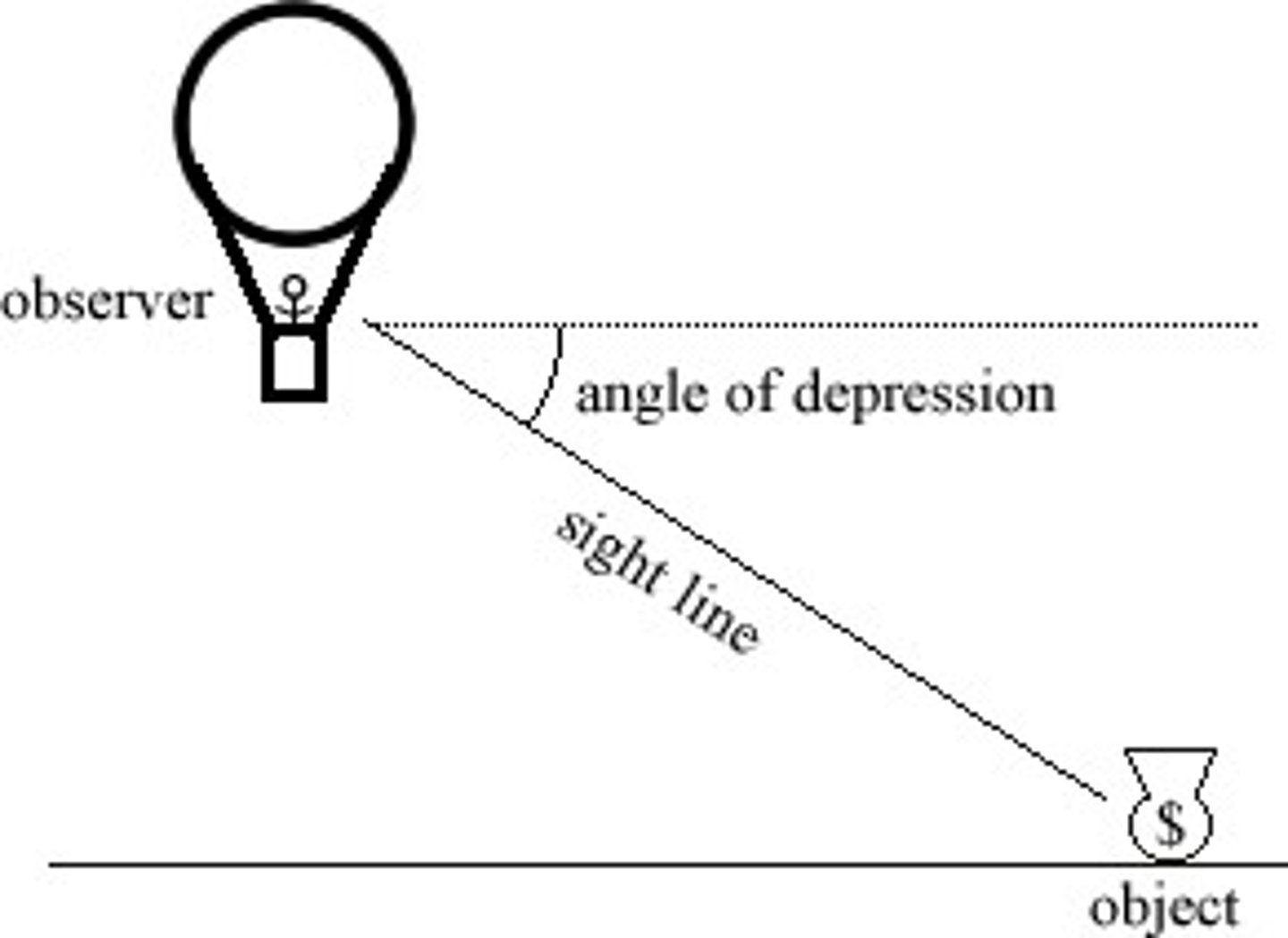
What is an Angle of Depression?

An angle measured from the horizontal down.

What is a Vector?

A quantity with a magnitude and a direction.

What is a scalar?

A quantity with only magnitude.

When writing a vector and scalar, how are each represented?

To distinguish between vectors and scalars, we will write the letters used to represent

vectors with boldface type, such as U or V. (When you write them on paper,

put an arrow above them. The magnitude of a vector is represented

with absolute value symbols. For example, the magnitude of V is written |V|.

If V is a vector in standard position and is the angle measured from the positive

x-axis to V, then the horizontal and vertical vector components of V are given by what?

If V is a vector in standard position and ∅ is the angle measured from the positive

x-axis to V, then the horizontal and vertical vector components of V are given by

|Vx| = V cos ∅ and |Vy| = sin ∅

When an object is stationary (at rest), we say it is in a state of static equilibrium.

When an object is in this state, the sum of the forces acting on the object must be what?

When an object is stationary (at rest), we say it is in a state of static equilibrium.

When an object is in this state, the sum of the forces acting on the object must be

equal to the zero vector 0.

If a constant force F is applied to an object and moves the object in a straight line a distance d, then the work W performed by the force is ?

If a constant force F is applied to an object and moves the object in a straight line a distance d, then the work W performed by the force is

W = (F cos ∅) (d)

where ∅ is the angle between the force F and the line of motion of the object.

What is the Reference Angle Theorem?

A trig function of an angle and its reference angle are the same, except, perhaps, for a difference in sign.

How many degrees are in one radian?

57.3° is equal to one radian.

To find the radian measure of any central angle, we must find how many radii are

in the arc it cuts off. What is the formula to do this?

To do so, we divide the arc length by the radius.

If the radius is 2 centimeters and the arc cut off by central angle ∅ is 6 centimeters, then the radian measure of ∅ is

∅ = s/r

= 6/2

=3 rad

How many radians are in 360°?

2π

How many radians in one degree?

1° = π/180

How do you convert radians to degrees?

Multiply by 180/π

What is the formula for arc length?

s = r∅

r = the radius

∅ is in radians

s = arc length

this is the reworked formula

∅ = s/r which is the ratio of the circle perimeter to the radius.

If we are working with relatively small central angles in circles with large radii, we can use the length of the intercepted arc to approximate the length of the associated chord.

The chord is a line drawn which will create a triangle, but closely follows the circle arc because of the narrow slice.

What is the formula for the area of a sector?

A = 1/2(r² x ∅)

What is the formula for linear velocity?

v = s/t

s = distance

t = time

What is the formula for angular velocity?

ω = ∅/t

ω is omega

∅ is measured in radians

t is time

What is the definition of amplitude?

A = (1/2) x |M-n|

M = greatest value of y is M

m = the least value of y is m

What is a asymptote?

a line that continually approaches a given curve but does not meet it at any finite distance

What is an even function?

What is an odd function?

An even function is a function for which

f(-x) = f(x) for all x in the domain of f

The graph of an even function is symmetric about the y-axis.

An even function is a function for which replacing x with x leaves the expression

that defines the function unchanged

*******************************************

An odd function is a function for which

f(-x) =f(x) for all x in the domain of f

The graph of an odd function is symmetric about the origin.

An odd function is a function for which replacing x with -x changes the sign of the

expression that defines the function

If a function is odd, then every time the point (x, y) is on the graph, so is the point (-x, -y)

The graph of the sine function illustrates how the ____________ of a point on the unit circle

varies with ____ _________.

y coordinate, arc length

To calculate the amplitude for a function, take half the __________ of the ___________

value and the __________ value of the function.

difference, greatest, least

A function is even if the opposite input results in an ________ output. A function is odd if

the opposite input results in the _________ output.

equal, opposite

Which trigonometric functions do not have real zeros?

secant and cosecant

They are parabolas with their lowest point at 1

Which trigonometric functions have a period of 2π?

sine, cosine, secant, and cosecant

Which functions are even?

f(-x) = f(x)

cos (-x) = cos x

sec (-x) = sec x

Which functions are odd?

f(-x) = -f(x)

sin(-x) = -sin x

csc(-x) = -csc x

tan(-x) = -tan x

cot(-x) = -cot x

Concerning amplitude of A sin x what can we say?

we can say that if A > 0, then

the graphs of y = Asinx and y = Acosx will have amplitude A and range [-A, A].

Concerning amplitude of -A sin x what can we say?

If A < 0, then the graphs of y = A sin x and y = A cos x will be sine and cosine graphs that have been reflected about the x-axis. The amplitude will be |A|.

In this function A sin (x), what is x called?

x is called an argument.

If A is any real number and B > 0, then the graphs of y = A sin Bx and y = A cos Bx will have an Amplitude and Period of what?

Amplitude = |A|

and

Period = 2π/B

What is a horizontal translation?

It seems that the graph of y = sin (x = π/2) is shifted π/2 units to the left of the graph

of y = sin x. We say the graph of y = sin (x + π/2) has a horizontal translation, or

horizontal shift, of-π/2, where the negative sign indicates the shift is to the left (in the

negative direction).

If C is any real number and B > 0, then the graphs of y = sin (Bx + C) and y = cos (Bx + C) will have a period, horizontal shift, and phase of what?

Period = 2π/B

Horizontal shift = -C/B

Phase = C

What is the period of sin, cos, sec, csc?

2π

What is the period of tan and cot?

π

Given a sine or cosine graph, the horizontal distance between a maximum point and the following minimum point is equal to______ the ________

Given a sine or cosine graph, the horizontal distance between a maximum point and the following minimum point is equal to half the period.

Given a sine or cosine graph, the vertical translation is equal to the _________ of the

maximum and minimum values.

Given a sine or cosine graph, the vertical translation is equal to the average of the

maximum and minimum values.

What is a one-to-one function?

If y = f (x) is a one-to-one function, then the inverse of f is also a function and can

be denoted by y = f-¹ (x).

The original function must pass the horizontal line test and the inverse must pass the vertical line test.

When graphing or utilizing the inverse sin function, what inter do we restrict it too?

-π/2 ≤ y ≤ π/2

When graphing or utilizing the inverse cos function, what inter do we restrict it too?

0 ≤ x ≤ π

What is the notation for inverse sin, cos, tan?

The notation used to indicate the inverse cosine function is as follows:

Notation Meaning

y = cos-¹ x

y = sin-¹ x

y = tan-¹ x

In words: y is the angle between 0 and π, inclusive, whose cosine is x.

In words: y is the angle between -π/2 and π/2, inclusive, whose cosine is x.

In words: y is the angle between -π/2 and π/2, inclusive, whose tangent is x.

When graphing or utilizing the inverse tan function, what interval do we restrict it too?

-π/2 ≤ y ≤ π/2

To find the inverse of a function, ____________ the coordinates in each ordered pair for the function.

To find the inverse of a function, reverse the coordinates in each ordered pair for

the function.

The graph of the inverse of a function is a ___________ of the graph of the function

about the line _______.

The graph of the inverse of a function is a reflection of the graph of the function

about the line y = x.

What is a counter example?

To show that a statement is

not an identity is usually much simpler. All we must do is find a single value of the

variable for which each expression is defined, but which makes the statement false.

This is known as finding a counterexample.

How do you calculate the amplitude of a function?

A = 1/2 (greatest-least)

What are the even Trig functions?

cos(-x) = cos x

sec(-x) = sec x

all others are negative

What are the Pythagorean identities?

cos²∅ + sin²∅ =1

sin∅ = √(1 - cos²∅)

cos²∅ = √(1-sin²∅)

1 + tan² = sec²

1+ cot² = csc²

sin² = 1 - cos²

cos² = 1 - sin²

What is the formula for sin (A-B)?

sin (A-B) = sinA*sinB - cosA*cosB

What is the formula for sin (A+B)

sin (A+B) = sinA*sinB + cosA*cosB

What is the formula for cos (A-B)?

cos (A-B) = cosA*cosB + sinA*sinB

What is the formula for cos (A+B)?

cos (A-B) = cosA*cosB - sinA*sinB